Задача 9
Исследовать на сходимость числовой ряд:  .
.
Числовым рядом называется выражение
 , (1)
, (1)
где числа 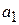 ,
, 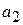 , … ,
, … ,  , … , называемые членами ряда, образуют известную числовую последовательность.
, … , называемые членами ряда, образуют известную числовую последовательность.
Числовой ряд (1) называется сходящимся, если сумма 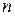 первых его членов
первых его членов  при
при 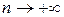 имеет предел.
имеет предел.
Этот предел называется суммой сходящегося ряда.
Если же  не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.
I. Необходимый признак сходимости. Если ряд сходится, то
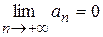 .
.
Достаточный признак расходимости для всякого ряда. Если же  , то ряд расходится.
, то ряд расходится.
Для числовых рядов с положительными членами ( ), при исследовании их сходимости, употребительны следующие достаточные признаки сходимости:
), при исследовании их сходимости, употребительны следующие достаточные признаки сходимости:
II. Признак сравнения. Если ряд с положительными членами
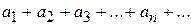 (а)
(а)
сравнить с другим рядом с положительными членами
 (b)
(b)
сходимость или расходимость которого известна, и если, начиная с некоторого номера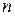 :
:
1)  и ряд (b) сходится, то и ряд (а) также сходится;
и ряд (b) сходится, то и ряд (а) также сходится;
2)  и ряд (b) расходится, то ряд (а) также расходится.
и ряд (b) расходится, то ряд (а) также расходится.
При использовании этого признака исследуемый ряд часто сравнивается или с бесконечной геометрической прогрессией
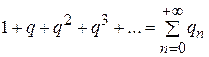 ,
,  , (2)
, (2)
которая при  сходится, а при
сходится, а при 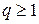 расходится, или с расходящимся гармоническим рядом
расходится, или с расходящимся гармоническим рядом
 . (3)
. (3)
Знакопеременный ряд (с членами разных знаков)
 (4)
(4)
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений его членов
 (5)
(5)
Знакопеременный сходящийся ряд (4) называется неабсолютно сходящимся, если ряд (5) расходится.
Всякий абсолютно сходящийся ряд есть ряд сходящийся.
III. Признак Даламбера. Если  , то при
, то при 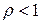 ряд сходится, а при
ряд сходится, а при  расходится. При
расходится. При 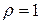 вопрос о сходимости ряда остается нерешенным.
вопрос о сходимости ряда остается нерешенным.
IV. Радикальный признак Коши. Если  , то при
, то при  ряд сходится, а при
ряд сходится, а при  расходится. При
расходится. При  признак ответа на вопрос о сходимости не дает.
признак ответа на вопрос о сходимости не дает.
V. Интегральный признак Коши. Ряд с положительными убывающими членами 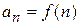 сходится или расходится, смотря по тому, сходится или расходится несобственный интеграл
сходится или расходится, смотря по тому, сходится или расходится несобственный интеграл  , где
, где 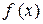 – непрерывная убывающая функция[2].
– непрерывная убывающая функция[2].
Этим признаком можно пользоваться, когда выражение общего члена 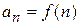 имеет смысл не только для целых положительных значений
имеет смысл не только для целых положительных значений 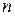 , но и для всех
, но и для всех 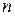 , больших некоторого положительного числа
, больших некоторого положительного числа  .
.
VI. Признак Лейбница. Знакочередующийся ряд (знаки членов которого строго чередуются) 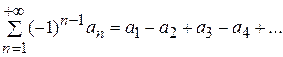 ,
,  сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если
сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е. если 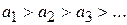 . и
. и 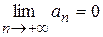 .
.
При практическом использовании рядов (сходящихся) обычно ограничиваются несколькими их первыми членами. Допускаемая при этом ошибка (остаток ряда) наиболее просто оценивается для знакочередующихся рядов:
Ошибка при замене суммы сходящегося знакочередующегося ряда суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.
Решение. Члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:  и
и 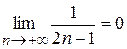 .
.
Поэтому, согласно признаку Лейбница, данный ряд сходится. Чтобы установить, сходится он абсолютно или неабсолютно, исследуем ряд с положительными членами  , составленный из абсолютных значений членов данного ряда.
, составленный из абсолютных значений членов данного ряда.
Применяя интегральный признак

заключаем, что ряд с положительными членами расходится.