Задача 10
Определить интервал сходимости степенного ряда: 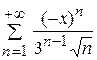 .
.
Ряд 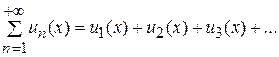 , члены которого являются функциями от переменной
, члены которого являются функциями от переменной 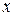 , называется функциональным.
, называется функциональным.
При различных значениях 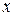 из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
Совокупность значений 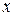 , при которых функциональный ряд сходится, называется его областью сходимости.
, при которых функциональный ряд сходится, называется его областью сходимости.
Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида
 (1)
(1)
или более общего вида
 (2)
(2)
Областью сходимости всякого степенного ряда является один интервал числовой оси, симметричный относительно точки 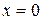 (для ряда 1) или
(для ряда 1) или 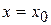 (для ряда 2), который может быть закрытым, открытым или полуоткрытым.
(для ряда 2), который может быть закрытым, открытым или полуоткрытым.
Для определения области сходимости функциональных рядов обычно вначале используется признак Даламбера, а затем те значения 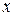 , для которых этот признак не решает вопроса о сходимости ряда (
, для которых этот признак не решает вопроса о сходимости ряда (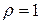 ), исследуются особо, посредством других признаков сходимости рядов.
), исследуются особо, посредством других признаков сходимости рядов.
Решение. По известному члену ряда 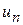 , заменяя в нем
, заменяя в нем 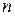 через
через 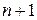 , находим следующий за ним член
, находим следующий за ним член 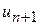 :
:
 ;
;  .
.
Далее, используя признак Даламбера, ищем предел
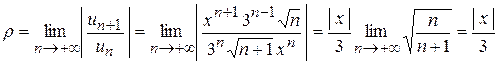
и определяем, при каких значениях 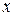 этот предел будет меньше единицы, т.е. решаем неравенство
этот предел будет меньше единицы, т.е. решаем неравенство 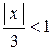 :
: 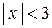 ;
; 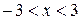 .
.
Согласно признаку Даламбера, при любом значении 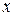 из найденного интервала данный ряд сходится (абсолютно), а при
из найденного интервала данный ряд сходится (абсолютно), а при 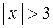 расходится.
расходится.
Граничные точки  этого интервала, для которых
этого интервала, для которых 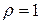 и признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.
и признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.
При 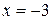 получим числовой ряд с положительными членами
получим числовой ряд с положительными членами 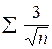 , который расходится, что следует из сравнения его с расходящимся гармоническим рядом
, который расходится, что следует из сравнения его с расходящимся гармоническим рядом  . (Каждый член исследуемого ряда больше соответствующего члена гармонического ряда.)
. (Каждый член исследуемого ряда больше соответствующего члена гармонического ряда.)
При получим числовой знакочередующийся ряд
получим числовой знакочередующийся ряд  , который сходится, согласно признаку Лейбница. (Члены этого ряда убывают по абсолютному значению, стремясь к нулю.)
, который сходится, согласно признаку Лейбница. (Члены этого ряда убывают по абсолютному значению, стремясь к нулю.)
Следовательно, интервалом сходимости данного степенного ряда является полуоткрытый интервал  .
.