Задача 11
Разложить в степенной ряд Тейлора функцию:  при
при 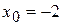 .
.
Рядом Тейлора для функции 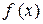 в окрестности точки
в окрестности точки 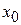 называется степенной ряд относительно двучлена
называется степенной ряд относительно двучлена 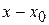 вида
вида
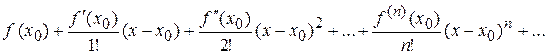 .
.
Формально ряд Тейлора можно написать для всякой функции, которая в окрестности точки 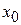 имеет производные любого порядка. Однако этот ряд будет сходиться в породившей его функции
имеет производные любого порядка. Однако этот ряд будет сходиться в породившей его функции 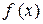 только при тех значениях
только при тех значениях 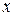 , при которых остаточный член
, при которых остаточный член 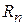 формулы Тейлора для этой функции при неограниченном возрастании
формулы Тейлора для этой функции при неограниченном возрастании 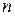 стремится к нулю.
стремится к нулю.
При 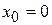 ряд Тейлора есть степенной ряд относительно независимой переменной
ряд Тейлора есть степенной ряд относительно независимой переменной 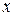 :
:
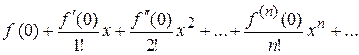 ,
,
который принято называть рядом Маклорена.
Для разложения данной функции в ряд Тейлора нужно:
а) написать ряд Тейлора для данной функции, т.е. вычислить значения этой функции и ее производных при 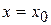 и подставить их в общее выражение ряда Тейлора для произвольной функции;
и подставить их в общее выражение ряда Тейлора для произвольной функции;
б) исследовать остаточный член 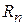 формулы Тейлора для данной функции и определить совокупность значений
формулы Тейлора для данной функции и определить совокупность значений 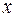 , при которых полученный ряд сходится к данной функции (т.е. при которых
, при которых полученный ряд сходится к данной функции (т.е. при которых 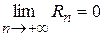 ).
).
Для многих функций, употребляемых в практических применениях математического анализа, интервал сходимости ряда Тейлора полностью совпадает с совокупностью тех значений 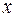 , при которых соответствующий остаточный член
, при которых соответствующий остаточный член 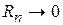 , когда
, когда 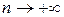 , т.е. для многих функций каждая точка
, т.е. для многих функций каждая точка 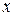 сходимости ряда Тейлора является и точкой сходимости этого ряда к породившей его функции. Поэтому при разложении многих функций в ряд Тейлора можно вместо исследования соответствующего остаточного члена
сходимости ряда Тейлора является и точкой сходимости этого ряда к породившей его функции. Поэтому при разложении многих функций в ряд Тейлора можно вместо исследования соответствующего остаточного члена 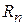 , что во многих случаях весьма затруднительно, исследовать сходимость самого ряда Тейлора, как обычного степенного ряда.
, что во многих случаях весьма затруднительно, исследовать сходимость самого ряда Тейлора, как обычного степенного ряда.
Решение. а) Вычисляем значения данной функции и ее производных при 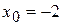 :
:
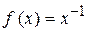

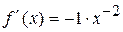
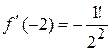
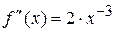

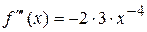
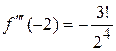
.......................................... ............................
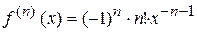
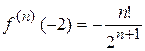
.......................................... ............................
Подставляя эти значения в ряд Тейлора для произвольной функции, получим
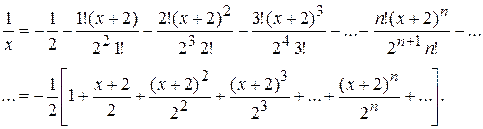
б) Исследуем сходимость полученного ряда по признаку Даламбера:
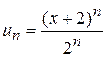 ;
;  .
.
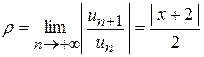 ;
; 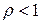 , если
, если  .
.
Решая это неравенство, находим интервал 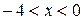 . Границы этого интервала исследуем особо. Подставляяв ряд
. Границы этого интервала исследуем особо. Подставляяв ряд 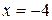 , затем
, затем 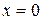 , получим числовые ряды
, получим числовые ряды 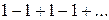 и
и 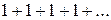 , которые расходятся, так как у них не выполняется необходимое условие сходимости ряда
, которые расходятся, так как у них не выполняется необходимое условие сходимости ряда 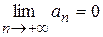 .
.
Следовательно, интервал сходимости полученного ряда Тейлора для данной функции есть 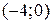 . Исследуя остаточный член
. Исследуя остаточный член 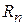 формулы Тейлора для данной функции, можно убедиться, что в указанном интервале полученный ряд сходится именно к данной функции.
формулы Тейлора для данной функции, можно убедиться, что в указанном интервале полученный ряд сходится именно к данной функции.