Решение.
1. Вычислим точечные оценки требующихся параметров
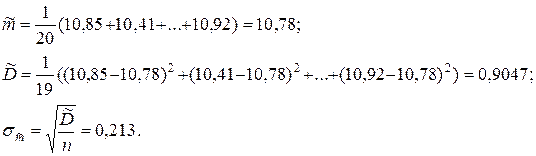
2. По таблице функции Лапласа для  находим
находим  = 1,282. Тогда
= 1,282. Тогда
 .
.
Доверительные границы для математического ожидания:

Доверительный интервал для математического ожидания:
 = (10,51 ; 11,05).
= (10,51 ; 11,05).
3. Найдем приближенно 80% - й доверительный интервал для дисперсии, считая, что величина X распределена по нормальному закону.
Имеем:  = 1,282.
= 1,282.  .
.
Тогда доверительный интервал для дисперсии будет равен
 .
.
Соответствующий интервал для среднего квадратического отклонения:
 = (0,73; 1,132).
= (0,73; 1,132).
4. Найдем точный доверительный интервал для математического ожидания, считая X нормальной величиной.
Имеем n = n - 1 = 19;  По таблице квантилей Т-распределения Стьюдента при n = 19,
По таблице квантилей Т-распределения Стьюдента при n = 19,  находим
находим  . Отсюда
. Отсюда  .
.
Расхождение точного и приближенного доверительных интервалов незначительное. Если сохранить точность до второго знака после запятой, то доверительные интервалы, найденные точным и приближенным методами, совпадают:
 = (10,51; 11,05).
= (10,51; 11,05).
5. Найдем точный доверительный интервал для дисперсии, считая X нормальной величиной.
Имеем 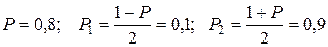 .
.
Для  и
и  при n = n - 1 = 19 по таблице квантилей хи-квадрат распределения находим, соответственно,
при n = n - 1 = 19 по таблице квантилей хи-квадрат распределения находим, соответственно, 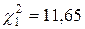 ;
;  .
.
Тогда 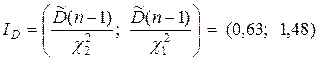 .
.
Соответствующий доверительный интервал для среднего квадратического отклонения:
 = (0,794; 1,217).
= (0,794; 1,217).