рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Логарифм бесконечного произведения.

Реферат Курсовая Конспект

Выберите учебное заведение

Логарифм бесконечного произведения.

Логарифм бесконечного произведения. - раздел Математика, Представление в виде степенного ряда Пусть ...

Пусть

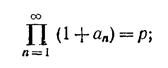
верно ли, что

Здесь log z главное значение логарифма числа z, т. е. значение, мнимая часть которого лежит между —π и π

Ответ будет, очевидно, утвердительным, если все числа а_пдействительны и положительны, поскольку тогда все логарифмы имеют свое обычное арифметическое значение. Но в общем случае формула требует модификации.

Пусть р_п обозначает п-е частичное произведение, и пусть 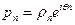, так что р_п и ρ_n стремятся к пределам и то же относится к аргументу φ_n, если его значения выбраны надлежащим образом. Пусть

тогда, так как а_л→0 при n→∞, то и θ_n →0 Положим

Очевидно,

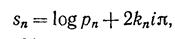
где k_n — целое число, и 2k_nπ = θ₁ +…+ θ₂ – φ_n. так что

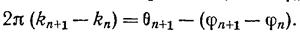
Поскольку правая часть стремится к нулю, при достаточно большом n

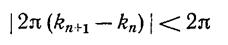
и, следовательно, k_n₊₁ = k_n (напомним, что все k_n — целые числа). Таким образом, k_n имеет при достаточно большом п постоянное значение, скажем k, т. е. 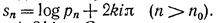Следовательно,

Сумма ряда есть, таким образом, некоторое значение, но не обязательно главное значение, логарифма произведения.

Заметим, что в ходе доказательства мы получили для всех достаточно больших значений N равенство

Если мы начнем с ряда логарифмов и положим

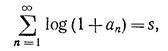
то после перехода к экспоненциалам в формуле (1), мы получим равенства

Равномерная сходимость бесконечных произведений.

Бесконечное произведение

где сомножители — функции переменного z, вещественного или комплексного, называется равномерно сходящимся в некоторой области значений z, если частичное произведение

равномерно сходится в этой области к некоторому пределу, нигде не равному нулю.

Вот простейший признак равномерной сходимости произведения.

Произведение

равномерно сходится в каждой области, в которой ряд равномерно сходится к ограниченной функции.

Доказательство состоит в пересмотре аргументов ранее доказанной теоремы с точки зрения равномерности. Пусть М — верхняя грань суммы

в рассматриваемой области. Тогда

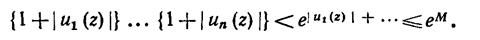
Полагая

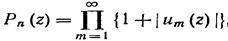
мы видим, что

Следовательно, ряд равномерно сходится, и доказательство завершается так же, как в прошлый раз

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Представление в виде степенного ряда

Представление Пуассона для гармонических функций... Представление Пуассона для гармонических функций принадлежащих некоторым... Пусть известно лишь что функция U z гармонична в круге z lt Замечательно что часто е вс же можно...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Логарифм бесконечного произведения.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Представление в виде степенного ряда
Пусть U(z) – вещественная функция, гармоническая в круге . Тогда можно построить другую веществе

Формула Пуассона
Формулу, которую мы вывели в предыдущем пункте, можно записать в замкнутом виде. Если R > 1, то мы легко находим, что при r < 1

Свойства суммируемости гармонических функций, заданных формулой Пуассона
Сначала получим некоторые грубые результаты, достаточные для многих рассмотрений. Ядро Пуассона

Первоначальное изучение граничного поведения
Ядро Пуассона Рr(θ) обладает и четвертым свойством: d) Для любого σ > О Рr(θ)→0 равномерно для σ≤│θ│

Формула Коши
Теорема. Пусть D — область на комплексной плоскости с кусочно-гладкой границей , функция

Формула Коши-Грина
f(z)= ς=ξ+iμ z Є inf Г Доказательство

Весовое пространство аналитических в круге функций
Пусть обозначим через

Интегральное представление гармонических функций
Пусть – множество всех гармонических в

ГАРМОНИЧЕСКИ СОПРЯЖЕННАЯ ФУНКЦИЯ
Пусть дана функция U(z), гармоническая в {|r| < 1}, для которой имеет место одно из рассматриваемых представлений. Мы приступаем к исследованию граничного поточечного повед

Формула для гармонически спряженной функции
Предположим, что ,

Бесконечные числовые произведения комплексных чисел и их сходимость.
Бесконечное произведение есть выражение вида (1+а1)(1+а2)(1+а3) .... (1) содержащее бесконечно много сомножителей. Мы обозначаем его через

Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке
А. Произведение Бляшке Если .., и бесконечное произведение

Единице
Пусть так что

Аналитической в единичном круге
Теорема. Пусть функция F(z) регулярна в круге {|z|<1} и zп — её нули в этом круге, |zn| < 1. Предположим, что интегралы

ОБЛАСТИ, ОГРАНИЧЕННЫЕ СПРЯМЛЯЕМОЙ ЖОРДАНОВОИ КРИВОЙ
Рассмотрим теперь область , G ограниченную спрямляемой жордановой кривой. Пусть Ф— конформное отображение единичного круга на G — область, ограниченную жордановой спрямляемой кривой

Образы множеств меры нуль на единичной окружности
Если А — дуга кривой Г, то Ф взаимно-однозначно отображает некоторую дугу j окружности {|z|=1} на Ʌ. Само определение длины дуги теперь нам дает

Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы
Теорема (Харди). Степенной ряд функции Ф(z) абсолютно сходится вплоть до {|z|= 1}. Дoказательство. По подпункту 1° имеем