рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Свойства суммируемости гармонических функций, заданных формулой Пуассона

Реферат Курсовая Конспект

Выберите учебное заведение

Свойства суммируемости гармонических функций, заданных формулой Пуассона

Свойства суммируемости гармонических функций, заданных формулой Пуассона - раздел Математика, Представление в виде степенного ряда Сначала Получим Некоторые Грубые Результаты, Достаточные Для Многих Рассмотр...

Сначала получим некоторые грубые результаты, достаточные для многих рассмотрений.

Ядро Пуассона

обладает следующими свойствами:

а) Р_r(φ)>0, r< 1;

b)Р_r(φ+2π)= Р_r(φ)

с) 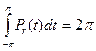для любого r<1.

Свойства а) и b) очевидны, а с) следует из разложения в ряд для Pr(φ).

Если 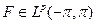то удобно считать, что функция F периодически продолжена на всё множество R: F(t+2π)=F(t). Отныне будем это предполагать.

Теорема. Если p≥l, 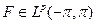, a , то функция U(z) — гармоническая в круге {|z|<1}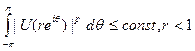

Доказательство.

Пусть . Тогда для 0 ≤r < 1 имеем

Непосредственно проверяется, что функция U(z) гармонична в {|r|< 1}, так как ряд сходится равномерно во внутренности круга. (Если функция F—вещественная, то ряд, очевидно, является вещественной частью аналитической функции, которая легко выписывается.)

Для данного r < 1 в силу свойства b) и 2π-периодичности функции F мы можем, кроме того, записать

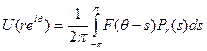
Возьмём теперь 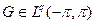,||G||_q=1, так что (для любого фиксированного r; функция G, конечно, будет зависеть от r)

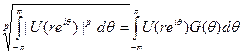
По теореме Фубини интеграл справа равен

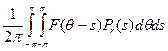
что по модулю не превосходит

(в силу выбора G и свойства с)).

Наконец,

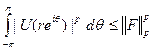
что и требовалось доказать

Теорема. Пусть μ — конечная вещественная мера на [-π,π]. Тогда функция

гармонична в {|r|< 1} и

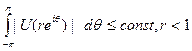
Доказательство.

Гармоничность устанавливается так же, как и выше. Пусть дано r, и пусть функция 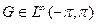, 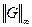= 1, такова, что

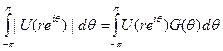-п

Интеграл в правой части по теореме Фубинн равен

и в силу а)—с) по модулю не превосходит

Вот и всё.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Представление в виде степенного ряда

Представление Пуассона для гармонических функций... Представление Пуассона для гармонических функций принадлежащих некоторым... Пусть известно лишь что функция U z гармонична в круге z lt Замечательно что часто е вс же можно...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства суммируемости гармонических функций, заданных формулой Пуассона

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Представление в виде степенного ряда
Пусть U(z) – вещественная функция, гармоническая в круге . Тогда можно построить другую веществе

Формула Пуассона
Формулу, которую мы вывели в предыдущем пункте, можно записать в замкнутом виде. Если R > 1, то мы легко находим, что при r < 1

Первоначальное изучение граничного поведения
Ядро Пуассона Рr(θ) обладает и четвертым свойством: d) Для любого σ > О Рr(θ)→0 равномерно для σ≤│θ│

Формула Коши
Теорема. Пусть D — область на комплексной плоскости с кусочно-гладкой границей , функция

Формула Коши-Грина
f(z)= ς=ξ+iμ z Є inf Г Доказательство

Весовое пространство аналитических в круге функций
Пусть обозначим через

Интегральное представление гармонических функций
Пусть – множество всех гармонических в

ГАРМОНИЧЕСКИ СОПРЯЖЕННАЯ ФУНКЦИЯ
Пусть дана функция U(z), гармоническая в {|r| < 1}, для которой имеет место одно из рассматриваемых представлений. Мы приступаем к исследованию граничного поточечного повед

Формула для гармонически спряженной функции
Предположим, что ,

Бесконечные числовые произведения комплексных чисел и их сходимость.
Бесконечное произведение есть выражение вида (1+а1)(1+а2)(1+а3) .... (1) содержащее бесконечно много сомножителей. Мы обозначаем его через

Логарифм бесконечного произведения.
Пусть верно ли, что

Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке
А. Произведение Бляшке Если .., и бесконечное произведение

Единице
Пусть так что

Аналитической в единичном круге
Теорема. Пусть функция F(z) регулярна в круге {|z|<1} и zп — её нули в этом круге, |zn| < 1. Предположим, что интегралы

ОБЛАСТИ, ОГРАНИЧЕННЫЕ СПРЯМЛЯЕМОЙ ЖОРДАНОВОИ КРИВОЙ
Рассмотрим теперь область , G ограниченную спрямляемой жордановой кривой. Пусть Ф— конформное отображение единичного круга на G — область, ограниченную жордановой спрямляемой кривой

Образы множеств меры нуль на единичной окружности
Если А — дуга кривой Г, то Ф взаимно-однозначно отображает некоторую дугу j окружности {|z|=1} на Ʌ. Само определение длины дуги теперь нам дает

Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы
Теорема (Харди). Степенной ряд функции Ф(z) абсолютно сходится вплоть до {|z|= 1}. Дoказательство. По подпункту 1° имеем