Основные свойства определенных интегралов

Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл связан, согласно (3), (5) и (6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции y = f(x), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (12), считать определенный интеграл работой А силы f(x) (силы любого направления, а значит, и любого знака), когда точка приложения х этой силы перемещается вдоль оси ох из положения а в положение b (рис. 10).

 

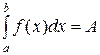(22)

 

 

Тогда сразу становятся очевидными следующие

Свойства определенных интегралов:

1) – число

(23)

(число А может быть любого знака).

2)

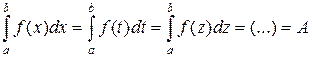
(24)

(переменную интегрирования в определенном интеграле можно обозначить как угодно – результат не изменится).

3)

(25)

(ибо если перемещение точки отсутствует, то работа любой силы f(x) равна нулю).

4)

(26)

(ибо если сила отсутствует, то и работа отсутствует).

5)

(27)

(ибо работа постоянной единичной силы численно равна перемещению точки под действием этой силы).

6)

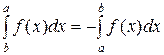
(28)

 

7) Для любых трех чисел a,b и c ( при всех возможных их расположениях относительно друг друга, см рисунки ниже ) справедливо равенство

 

 

 

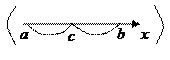
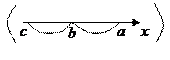
(29)

 

8) (30)

 

9)

(31)

 

10) Если f(x) ≤ g(x) для всех xÎ[a; b], то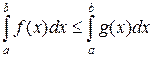

(32)

(физический смысл последних пяти свойств продумать самостоятельно).

11) Пусть m = [f(x)]_наим и М = [f(x)]_наиб – соответственно наименьшее и наибольшее значения функции f(x) на промежутке [a; b]. Тогда

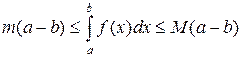
(33)

Действительно, так как m ≤ f(x)≤ M для всех xÎ [a; b], то применяя свойство (32) и затем свойства (31) и (27), мы и получим двойное неравенство (33). Это неравенство часто используется для прикидки (грубой оценки) величины .

12) ( теорема о среднем ). Если функция f(x) непрерывна на отрезке [a; b], то на этом отрезке найдется такая точка , что справедливо следующее равенство:

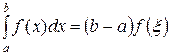
(34)

 

Пример 1. Оценить величину .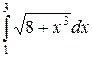

Решение. Так как функция 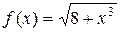монотонно возрастает на отрезке [1; 3], то Поэтому по формуле грубой оценки (33) получаем:

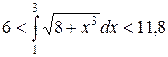
Пример 2. Оценить величину .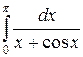

Решение. Минимальное m и максимальное M значения функции на промежутке [0; p] не очевидны, так как с возрастанием х в выражении x + cos x первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции y, найдем ее производную:

.

Так как sin x ≤ 1 для всех х, то для всех х. А значит, функция убывает на всей области своего определения, в том числе и на отрезке [0; p]. Таким образом, на отрезке [0; p]

Следовательно, оценка (4.18) для данного интеграла имеет вид: