рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Методы численного интегрирования.
Реферат Курсовая Конспект
Методы численного интегрирования.
Методы численного интегрирования. - раздел Математика, Вычисление несобственных интегралов С Целью Ускорения Вычислений Интегралов Численными Методами Подынтегральную Ф...
С целью ускорения вычислений интегралов численными методами подынтегральную функцию удобно представлять в наиболее простом виде, используя функции упрощения функциями  и
и 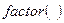 .Возможны случаи, когда система до упрощения не может вычислить неопределенный интеграл и легко его определяет после упрощения.
.Возможны случаи, когда система до упрощения не может вычислить неопределенный интеграл и легко его определяет после упрощения.
Численное интегрирование необходимо в следующих случаях:
- невозможно воспользоваться формулой Ньтона-Лейбница, т.е. первообразная не выражается через элементарные функции;
- аналитическое выражение интеграла слишком сложное;
- подынтегральная функция задана в табличной форме или в виде матрицы.
Так как с геометрической точки зрения определённый интеграл 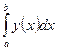 представляет собой площадь криволинейной трапеции. Идея методов численного интегрирования сводится к разбиению интервала [a; b] на множество меньших интервалов и нахождению искомой площади как совокупности элементарных площадей, полученных на каждом частичном промежутке разбиения. В зависимости от использованной аппроксимации получаются различные формулы численного интегрирования, имеющие различную точность. Приближенные формулы численного интегрирования называются квадратурными.
представляет собой площадь криволинейной трапеции. Идея методов численного интегрирования сводится к разбиению интервала [a; b] на множество меньших интервалов и нахождению искомой площади как совокупности элементарных площадей, полученных на каждом частичном промежутке разбиения. В зависимости от использованной аппроксимации получаются различные формулы численного интегрирования, имеющие различную точность. Приближенные формулы численного интегрирования называются квадратурными.
Метод вычисления интеграла выбирает пользователь. В этом особенность системы Matlab. С помощью Matlab вы имеете возможность сравнивать различные методы численного интегрирования. Существует ряд способов численного интегрирования.
Общая формула численного интегрирования

Где xR(f) – остаточный член.
Чаще всего используются формулы с равноотстоящими узлами, когда отрезок интегрирования
[a; b] разбивается на n равных частей системой точек
хi=x0+ih (i=0,1,2,…,n); х0=a; хn=b; h=(b-a)/n
Метод трапеций
Здесь используется линейная аппроксимация, т.е. график функции 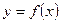 представляется в виде ломаной, соединяющей точки уi. Формула трапеций при постоянном шаге
представляется в виде ломаной, соединяющей точки уi. Формула трапеций при постоянном шаге 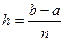 , где n – число участков, имеет вид
, где n – число участков, имеет вид 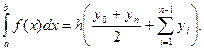
Остаточный член формулы трапеций: 
Как показывает это выражение, формула трапеций является точной для линейных функций, поскольку вторая производная, входящая как множитель в выражение остаточного члена, для этих функций тождественно равна нулю
В Matlab данная формула трапеций реализуется функциями:
trapz(y) - возвращает определённый интеграл, используя интегрирование методом трапеций с единичным шагом между отсчетами. Если У – вектор, то trapz(y) возвращает интеграл элементов вектора У, если У – матрица, то trapz(y) возвращает вектор-строку, содержащую интегралы каждого столбца этой матрицы.
trapz(x,y) – возвращает интеграл от функции У по переменной Х по методу трапеций.
Пример. Вычислить интеграл 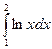
Решение:
x=1:0.1:2;
>> y=log(x);
>> trapz(x,y)
ans = 0.3859
Точное значение интеграла, который берётся аналитически, равно 0,3863
Узлы по оси Х могут быть и не равноотстоящими.
Пример: Вычисление интеграла с неравномерным шагом по Х
xn=[1:0.1:1.5,1.6:0.2:2];
>> yn=log(xn);
>> trapz(x,y)
ans = 0.3859
Найдем истинное значение интеграла с учетом остаточного члена. Для 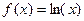 имеем
имеем
f’’(x)=-1/x2. При 1<ξ<2 вторая производная -1<f’’(ξ)<-1/4. Так как b-a=1, h=0.1, остаточный член 0,0002<Rтрап<0,0008. С учётом остаточного члена истинное значение интеграла заключено между
0,3859+0,0002 и 0,3859+0,0008 т.е. между 0,3861 и 0,3867 (его точное значение 0,3863)
Функция cumtrapz(x,y)выполняет кумулятивное (т.е. накопительное) суммирование по формуле трапеций.Где х, увекторы одной размерности, или х-вектор столбец, у – матрица.Она возвращает вектор, i-я компонента которого есть сумма первых i слагаемых формулы трапеций.
Вычисление интеграла на i-м шаге выполняется по формуле 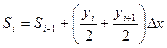
Si-1 – предыдущее значение интеграла;
Yi, Yi-1 – значение функции в начале и в конце интервала Δх;
Δх – шаг интегрирования на участке [Yi, Yi-1].
Пример. Накопительное суммирование по формуле трапеций.
x=1:0.1:2;
>> y=log(x);
>> cumtrapz(x,y)
ans =
0 0.0048 0.0186 0.0409 0.0708 0.1079 0.1517 0.2017 0.2576 0.3191 0.3859
Сравним полученный результат с точными значениями с переменным верхним пределом, равным x*(log(x)-1)+1. Чтобы вычислить по этой формуле, её необходимо «векторизовать»:
>> x.*(log(x)-1)+1
ans =
0 0.0048 0.0188 0.0411 0.0711 0.1082 0.1520 0.2021 0.2580 0.3195 0.3863
Разница между приближёнными и точными значениями не превосходит 0,004.
Более точная формула численного интегрирования с равноотстоящими узлами – формула Симпсона.
Метод Симпсона
Если подынтегральную функцию заменить параболой, то формула Симпсона с постоянным шагом интегрирования будет иметь вид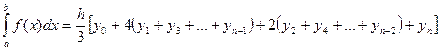
Остаточный член формулы Симпсона: 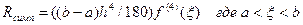
Как показывает это выражение, формула Симпсона является точной для многочленов степени не выше 3-й, четвёртая производная от которых тождественно равна нулю.
В Matlab формула Симпсона реализуется функциями:
quad(@fun,a,b) – возвращает численное значение определённого интеграла от заданной функции (@fun на отрезке [a; b]
Подынтегральная функция может задаваться с помощью дескриптора @, тогда она программируется в файле – функции, или с помощью апострофов, тогда она записывается в самой функции quad. Точность вычисления интеграла по умолчанию 10-6.
quad(@fun,a,b,tol) - возвращает численное значение определённого интеграла с заданной относительной погрешностью. Чтобы точно определить комбинацию относительной и абсолютной погрешности можно использовать вектор, состоящий из двух элементов tol=[rel_tol abs_tol].
quad(@fun,a,b,tol,trace) - возвращает численное значение определённого интеграла и при значении trace = 1 в процессе работы выдаётся последовательность строк вида [fcnt a b-a q] в которых показаны: количество вычислений интегрируемой функции; левый конец промежутка4 его длина; найденное значение интеграла по этому промежутку. Если trace = 0 этот параметр отключен.
Из описания способа вычислений функции quad вытекает, что невозможно ограничиться заданием значений интегрируемой функции в каких-то заранее известных узлах (как для trapz), а необходимо уметь вычислять её значения в любой точке интервала интегрирования. Невозможно также использовать остаточный член для оценки точности, достигнутой функцией quad, как это делалось выше для функции trapz, поскольку неизвестен окончательный шаг h, используемый при интегрировании. К тому же он не обязательно одинаков на всём отрезке интегрирования.
Пример. Вычислить и вывести на печать по методам трапеций и Симпсона значение интеграла
Решение:
x=0:0.0001:1;
>> y=1./(1+x.^2);
>> z=trapz(x,y)
z = 0.7854 % метод трапеций
quad('(1./(1+x.^2))',0,1)
ans = 0.7854 % метод Симпсона
Точное значение интеграла равно 0,785398163.
Как видно из примера полученные результаты являются практически точными, а сами вычисления просты.
Замечание:
Для обеспечения точности программы используется система двойного пересчёта: определенный интеграл вычисляется дважды-с произвольными шагами 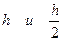 . Если при этом разность интегралов мала, то вычислительный процесс заканчивается, а значением интеграла считается то, которое вычислено с шагом
. Если при этом разность интегралов мала, то вычислительный процесс заканчивается, а значением интеграла считается то, которое вычислено с шагом  , в противном случае шаг уменьшается вдвое и сравниваются значения интеграла с шагами
, в противном случае шаг уменьшается вдвое и сравниваются значения интеграла с шагами 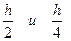 и так далее..
и так далее..
Функция quad(‘fun’,a,b)реализует метод Ньютона-Котеса восьмого порядка. Дает наиболее точное решение по сравнению с предыдущими методами и функциями. Имеет те же опции, что и функция quad(‘fun’,a,b,tol,trace)
Большое число методов и функций вычисления интегралов является достоинством системы MATLAB. При изучении методов интегрирования вы имеете возможность сравнить методы по их точности. Сравним точность методов на примере.
Пример:
Пусть подынтегральная функция имеет вид:
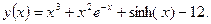
Необходимо вычислить интеграл в пределах от 0 до 10 методом трапеций, парабол (Симпсона) и Ньютона-Котеса. Использовать функции 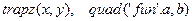 ,
, 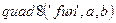 . Точность вычисления интеграла - по умолчанию
. Точность вычисления интеграла - по умолчанию 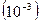 .
.
Результаты вычисления интеграла приведены в таблице:
| Функция | Значения интеграла |
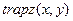
| 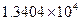 при при 
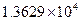 при при 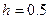
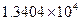 при при 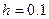
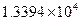 при при 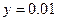
|
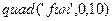
| 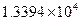
|

| 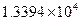
|
Точное значение неопределенного интеграла имеет вид:
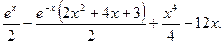
Численное значение интеграла, вычисленное по точной формуле в диапазоне от 0 до10, равно 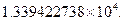
Из примера видно, что значение интеграла практически одно то же.
Правда, в методе трапеций шаг интегрирования должен быть не менее 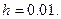
– Конец работы –
Эта тема принадлежит разделу:
Вычисление несобственных интегралов
Интегрирование в среде Mat lab... Нахождение неопредел нных и определ нных интегралов в среде Matlab... Вычисление несобственных интегралов...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Методы численного интегрирования.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов