Эти множества – независимые, т.к. в пределах 1 множества нет смежных двух вершин
Раскраски
Разнообразные задачи, возникающие при планировании производства , составлении графиков осмотра, хранении и транспортировке товаров могут быть представлены как
Задача о раскраске графа. Графы неориентированные и без петель(простые).
Граф G -  -хрономический, если его вершины могут быть раскрашены с помощью
-хрономический, если его вершины могут быть раскрашены с помощью  цветов (красок) так, что не найдутся две смежных вершин одного цвета. Наименьшее число
цветов (красок) так, что не найдутся две смежных вершин одного цвета. Наименьшее число  такое, что граф G -
такое, что граф G - -хрономический, называется хрономическим число графа
-хрономический, называется хрономическим число графа
G и обозначается 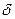 (G).Задача нахождений хрономического числа в графе – задача о раскраски графа. Соответствующие этому числу раскраски вершин разбивает множество вершин графа на z подмножества каждые из которых содержит вершины одного цвета.
(G).Задача нахождений хрономического числа в графе – задача о раскраски графа. Соответствующие этому числу раскраски вершин разбивает множество вершин графа на z подмножества каждые из которых содержит вершины одного цвета.
Эти множества – независимые, т.к. в пределах 1 множества нет смежных двух вершин.
В общем случае хрономическое число графа нельзя найти , зная лишь числа вершин и рёбер графа. Недостаточно знать и степень каждой вершины, чтобы вычислить хрономическое число графа. Однако, можно получить верхнего и нижнего оценки для хрономического графа.
1. Если  G) равно мощности наибольшего множества попарно несмежные вершины графа G , то оно совпадает с мощностью наибольшего множества вершин в G, которые могут быть окрашены в один цвет, и следовательно ,
G) равно мощности наибольшего множества попарно несмежные вершины графа G , то оно совпадает с мощностью наибольшего множества вершин в G, которые могут быть окрашены в один цвет, и следовательно ,
Ø 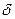 (G)
(G)  , где n –число вершин G, а
, где n –число вершин G, а 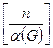 - наименьшее целое число, не превосходящее числа x.
- наименьшее целое число, не превосходящее числа x.
Ø Оценка Генера: 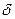 (G)
(G) , где m- число рёбер графа.
, где m- число рёбер графа.
2. Верхние оценки
Ø 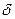 (G)
(G)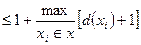 - Брукс
- Брукс
Формулировка задачи о раскраски на языке Булева (0-1, математического)
Программирования.
1, если вершина окрашена в цвет j, 0,в противном случае.Алгоритм раскраски
Связь с задачей раскраски Пусть нужно выбрать время проведения лекций по различным предметам с учетом…А. Точный алгоритм раскрашивания
1. Выбрать в графе G некоторое максимальное независимое множество вершин S. 2. Покрасить вершины S в очередной цвет 3. Применить процедуру Р к графу GSТеорема
Если граф G К-раскрашенный, то существует такие последовательности выбора множества S на шаге 1 процедуры Р, что применение процедуры Р к графу G построит не более, чем К –раскраску графа G.
В.Приближённый алгоритм последовательного раскрашивания
Алгоритм А имеет переборный характер. Имеет смысл использовать приближённый алгоритм, ……………..эффективен.
Алгоритм последовательного приближения
Выход: раскраска графа-массив С: ……..of 1….P For do Cвсе не раскрашеныС.Улучшенный алгоритм последовательной раскраски.
Вход: граф G Выход: раскраска графа –массив С: ……..of 1….PОбоснование
Заметим, что данный алгоритм отличается от предыдущего тем, что основной цикл идёт не по вершинам, по цветам : сначала , всё, что можно, красим в цвет 1 , затем в оставшиеся краски, всё, что можно в цвет 2 , и т.д. Алгоритмы В и С аналогичны.
Литература
- Кристофидес. Теория графов. Алгоритмический подход, изд-во Мир, М ,1978
- Ф.А. Новиков. Дискретная математика для программистов , С.П-б : Литература 2002-304-С
- Свален М. Тхуласираман К. Графы , сети и алогитмы.М; Мир , 1984;
- Р.Уилсон. Введение в теорию графов , Мир, М.1977.