Производящая функция
Пусть ап, п принадлежит N – последовательность. Этой последовательности поставим в соответствии ряд по целым числам Z. F*(z)=a+az+az +…+az+…
Предположим, что всегда существует неотрицательное α, для которого │ап│<α, и в этом случае всякой последовательности ап однозначно соответствует ряд f*(z) по целым степеням z. Соответствие между ап и f*(Z) в этом случае взаимно одно значимо, f*(Z) называется производящей функцией последовательности ап. Последовательность ап , представляет собой функцию от п, п=0,1. Обозначим ее через f(п) и будем повторять, что между совокупностями f(п) и f*(z) существует взаимно значимое соответствие.
Вводятся также производящие функции вида f(z)=a +a +a z/2+…+a z/п +п, называемые экспотенциольными производящими функциями.
f* и f допускает следующее обобщение φ*(z)=a φ (z)+a φ (z)+…+a φ(z)
Следующий частный случай:
φ(z)=1, φ(z)=z, φ (z)=z(z-1),…φ (z)=z(z-1)(z-n+1),…,φ*(z)=a +a +a (z-1)+…a (z-1)(z-n+1)/
распространяете на случай других многих переменных.
Производящую функцию f*(x)=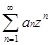 “называют преобразованием в Z” или Z – преобразованием. Иногда используют следующую функцию:
“называют преобразованием в Z” или Z – преобразованием. Иногда используют следующую функцию: 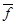 (z) =
(z) =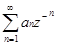 , называемую отрицательным z-преобразованием.
, называемую отрицательным z-преобразованием.
Кроме того используются экспонеидеальное z-преобразование: 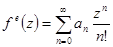

 . Пример. Пусть f(n)=1, n=0,1,2,…
. Пример. Пусть f(n)=1, n=0,1,2,… Тогда f*(z)=
Тогда f*(z)=
 . Имеем z-преобразование для f(n)=1 будет
. Имеем z-преобразование для f(n)=1 будет 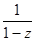

 .
.
Пусть 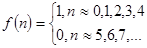


 ,тогда
,тогда  .
.
Существуют таблицы основных преобразований. Существует и обратное преобразование, т.е. коэффициенты разложения f*(z) в ряд Тейгора образует исходную последовательность f(n)/
Z-преобразование приводит к некоторому «символическому исчислению» или «…………….. исчислению» аналогично тому, которое получается с помощью преобразования Лапаса ( или Карсона – Лапаса) для функций непрерывных на отрезке, хотя Z-преобразование и применяется к последовательности.