Статически неопределимые балки.
Статически неопределимыми называются системы, реакции в которых не могут быть определены из уравнений равновесия твердого тела. В таких системах больше связей, чем это необходимо для равновесия. Степень статической неопределимости балки (не имеющей промежуточных шарниров – неразрезные балки) равна избыточному (лишнему) числу внешних связей (более трех).
 Раскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой оси балки. Записываем дифф-ное урав-ние куда входит в качестве неизвестной реакция RB и дважды его интегрируем: EJ
Раскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой оси балки. Записываем дифф-ное урав-ние куда входит в качестве неизвестной реакция RB и дважды его интегрируем: EJ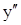 = RВ×x –
= RВ×x – 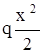 ; EJ
; EJ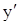 = RВ×
= RВ× –
– 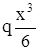 + С;
+ С;
EJy = RВ× –
– 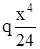 + С×х + D. Используем условия закрепления балки: х=0, y=0,
+ С×х + D. Используем условия закрепления балки: х=0, y=0, 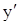 =0; x=L, y=0. Подставляем их в два последних уравнения, находи постоянные интегрирования С и D и неизвестную реакцию RB. Далее из урав-ний статики: HA=0; RA – q×L + RB=0; RB×L –
=0; x=L, y=0. Подставляем их в два последних уравнения, находи постоянные интегрирования С и D и неизвестную реакцию RB. Далее из урав-ний статики: HA=0; RA – q×L + RB=0; RB×L –  + MA=0; находятся RA и MA.
+ MA=0; находятся RA и MA.
 Уравнение совместности перемещений. Статически определимая балка, которая получается из статически неопределимой при удалении "лишнего" закрепления, называется основной системой. За "лишнюю" неизвестную можно взять любую из реакций. Приложив к основной системе заданные нагрузки добавляем условие, которое обеспечивает совпадение заданной балки и основной – уравнение совместности перемещений. Для рис.: yB=0, т.е. прогиб в точке В = 0. Решение этого уравнения возможно разными способами.
Уравнение совместности перемещений. Статически определимая балка, которая получается из статически неопределимой при удалении "лишнего" закрепления, называется основной системой. За "лишнюю" неизвестную можно взять любую из реакций. Приложив к основной системе заданные нагрузки добавляем условие, которое обеспечивает совпадение заданной балки и основной – уравнение совместности перемещений. Для рис.: yB=0, т.е. прогиб в точке В = 0. Решение этого уравнения возможно разными способами.
Способ сравнения перемещений. Определяется прогиб точки В (рис.) в основной системе под действием заданной нагрузки (q): yВq= . Далее рассматривается основная система под действием "лишней" неизвестной RB, и находится прогиб от действия RB:
. Далее рассматривается основная система под действием "лишней" неизвестной RB, и находится прогиб от действия RB:  . Подставляем в уравнение совместности перемещений: yB= yВq +
. Подставляем в уравнение совместности перемещений: yB= yВq +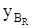 = 0, т.е.
= 0, т.е.  +
+ = 0, откуда RB=
= 0, откуда RB=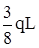 , далее остальные реакции находятся из уравнений статики.
, далее остальные реакции находятся из уравнений статики.
 Теорема о трех моментах. Используется при расчете неразрезных балок — балок на многих опорах, одна из которых неподвижна, остальные подвижны. Для перехода от статически неопределимой балки к статически определимой основной системе над –лишними опорами вставляются шарниры. Лишними неизвестные: моменты Mn, приложенные к концам пролетов над лишними опорами. Строятся эпюры моментов для каждого пролета балки от заданной нагрузки, рассматривая каждый пролет, как простую балку на двух опорах. Для каждой промежуточной опоры "n" составляется уравнение трех моментов:
Теорема о трех моментах. Используется при расчете неразрезных балок — балок на многих опорах, одна из которых неподвижна, остальные подвижны. Для перехода от статически неопределимой балки к статически определимой основной системе над –лишними опорами вставляются шарниры. Лишними неизвестные: моменты Mn, приложенные к концам пролетов над лишними опорами. Строятся эпюры моментов для каждого пролета балки от заданной нагрузки, рассматривая каждый пролет, как простую балку на двух опорах. Для каждой промежуточной опоры "n" составляется уравнение трех моментов:
 wn,wn+1–площади эпюр, an – расстояние от центра тяжести левой эпюры до левой опоры, bn+1 – расстояние от центра тяжести правой эпюры до правой опоры. Число уравнений моментов равно числу промежуточных опор. Совместное их решение позволяет найти неизвестные опорные моменты. Зная опорные моменты, рассматриваются отдельные пролеты и из уравнений статики находятся неизвестные опорные реакции. Если пролета всего два, то левый и правый моменты известны, т.к. это либо заданные моменты, либо они равны нулю. В результате получаем одно уравнение с одним неизвестным М1.
wn,wn+1–площади эпюр, an – расстояние от центра тяжести левой эпюры до левой опоры, bn+1 – расстояние от центра тяжести правой эпюры до правой опоры. Число уравнений моментов равно числу промежуточных опор. Совместное их решение позволяет найти неизвестные опорные моменты. Зная опорные моменты, рассматриваются отдельные пролеты и из уравнений статики находятся неизвестные опорные реакции. Если пролета всего два, то левый и правый моменты известны, т.к. это либо заданные моменты, либо они равны нулю. В результате получаем одно уравнение с одним неизвестным М1.