Понятие дифференциала.

Пусть функция f(x) дифференцируема в точке х₀:

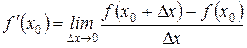Исходя из определения производной и теоремы о связи предела и бесконечно малой получаем:

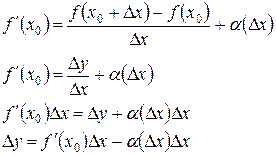
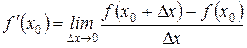при малых Dх само отношение 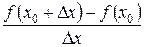сколь угодно мало отличается от и можно принять, что:

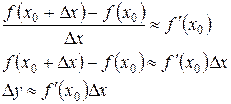
Итак, если функция f(x) дифференцируема в точке х₀, т. е. приращение Dу можно записать в виде суммы двух слагаемых (или опр. 2 §33):

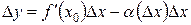, где .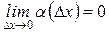

Первое слагаемое: 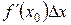является при Dх®0 бесконечно малой одного порядка с Dх, оно линейно относительно Dх:

Второе слагаемое: a(Dх)Dх при Dх®0 - бесконечно малая более высокого порядка, чем Dх:

.

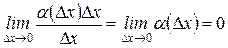Таким образом, первое слагаемое является главной частью приращения функции f(x), а вторым слагаемым можно пренебречь.

 

Определение 1: Дифференциалом функции y=f(x) в точке х₀, называется главная, линейная относительно Dх часть приращения функции dy=f¢(х₀)Dх.

 

Рассмотрим функцию y=x и вычислим её дифференциал по формуле dy=f¢(х₀)Dх:

dy=dх=1·Dх=Dх, то есть: dх=Dх. Будем называть дифференциалом независимой переменной дифференциал функции у=х.

Определение 2: Дифференциалом независимой переменной х называется приращение этой переменной: dх=Dх. Получаем:

dy=f¢(х₀)dх и 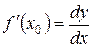.