Счетные и несчетные числовые множества

Теория множеств появилась в конце 19 века благодаря работам немецкого математика Георга Кантора (1845-1918). Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. Интуитивно мы понимаем множество как совокупность объектов. Кантор говорил: «Множество – это многое, понимаемое как единое». Примеры множеств: множество домов в городе, множество его жителей, множество звезд на небе и т.д.

Среди других множеств особое положение занимают так называемые числовые множества. Первое числовое множество, которое открылось человеческому сознанию, было множество натуральных чисел (обозначается буквой N): 1, 2, 3, … Идею их существования подсказывала сама природа (Nature). «Три дерева, три апельсина, три человека» – натуральное число «три» как-то связывало эти разные объекты, придавало им некую общность.

Но даже простые натуральные числа имели какую-то тайну. Это множество имело начало (число 1), однако не имело конца. Каким бы большим не было бы натуральное число, можно было бы получить еще большее, прибавив к нему единицу. Таким образом, множество натуральных чисел – бесконечное множество.

Существуют счетные и несчетные числовые множества. Очевидно, что множество, составленное из конечного числа натуральных чисел, будет счетным. Однако бывают и бесконечные счетные множества. Если элементам бесконечного множества можно поставить во взаимно однозначное соответствие числа натурального ряда, то такое множество называется счетным.

Например, множество четных чисел счетно. Числу 2 можно поставить в соответствие число 1, числу 4 – 2, числу 6 – 3 и т.д. Этот процесс можно продолжать до бесконечности.

Очевидно, что счетно и множество натуральных чисел, кратных трем (или четырем, или пяти…). Бесконечные множества, удовлетворяющие условию взаимно однозначного соответствия, называются равномощными.

Таким образом, множества четных чисел и натуральных чисел равномощны, хотя интуиция вроде бы подсказывает, что первое множество «меньше» второго. Одна из основных новаторский идей Кантора заключается в том, что соотношения, справедливые для конечных множеств, не применимы к бесконечным.

Древние индусы «изобрели» число ноль, а также отрицательные целые числа. Вместе с натуральными числами эти числа составляют множество целых чисел (обозначается латинской буквой Z). Натуральные числа и ноль образуют множество целых неотрицательных чисел (обозначается ).

Эти множества также являются счетными, так как можно установить взаимно однозначное соответствие между ними и множеством натуральных чисел, как показано в табл. 1.1.

 

Таблица 1.1

N
Z	– 3	– 2	– 1

 

Продолжая осваивать новые абстрактные понятия, люди ввели в обиход дробные числа, которые получают путем деления одного целого числа на другое. Такие числа называются рациональными, поскольку метод их получения вполне доступен пониманию (множество рациональных чисел обозначается буквой Q).

Кантор открыл, что множество рациональных чисел также счетно, хотя всюду плотно на числовой оси в отличие от множества натуральных чисел.

 

Таблица 1.2

							…
1/2	2/2	3/2	4/2	5/2	6/2	7/2	…
1/3	2/3	3/3	4/3	5/3	6/3	7/3	…
1/4	2/4	3/4	4/4	5/4	6/4	7/4	…
1/5	2/5	3/5	4/5	5/5	6/5	7/5	…
1/6	2/6	3/6	4/6	5/6	6/6	7/6	…
1/7	2/7	3/7	4/7	5/7	6/7	7/7	…
…	…	…	…	…	…	…	…

 

Все рациональные числа можно внести в таблицу с бесконечным количеством строк и столбцов (табл. 1.2). Если двигаться из левого верхнего угла по зигзагообразной траектории, нумеруя по пути ячейки числами натурального ряда, то можно показать взаимно однозначное соответствие между множествами натуральных и рациональных чисел.

Поскольку рациональные числа плотно заполняют всю числовую ось, долгое время считалось, что они удовлетворяют все практические нужды человека и необходимости во введении каких-либо новых числовых множеств не существует. Однако еще древнегреческим математикам удалось доказать существование так называемых иррациональных чисел, которые не могут быть выражены в виде целочисленной дроби (несоизмеримые соотношения).

Открытие иррациональных чисел легенда приписывает Гиппазию из Метапонта (V век до нашей эры), входившему в круг пифагорейцев – поклонников учения Пифагора. По преданию в тот момент, когда Гиппазий пришел к этому открытию, пифагорейцы находились в открытом море – и они выбросили Гиппазия за борт, обвинив его в том, что он привнес в мироздание элемент, противоречивший пифагорейскому учению о сводимости всех явлений природы к целым числам или к их отношениям.

 

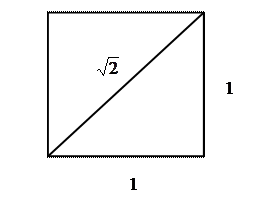
Рис. 1.1. Величина диагонали единичного квадрата

 

Математика древних греков носила геометрический характер. Из теоремы Пифагора следует, что диагональ единичного квадрата (рис. 1.1) равна по величине 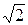. Доказательство того, что число 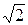несоизмеримо с единицей, т.е. иррационально, греческие математики проводили методом от противного.

Прежде чем приступать к этому доказательству, рассмотрим следующую лемму (греч. lemma – вспомогательное предложение, используемое при доказательстве теоремы).

Лемма 1.1. Квадрат четного числа – четное число, а квадрат нечетного числа – нечетное число.

Доказательство. Любое четное число можно записать как , а нечетное – как , Квадрат четного числа 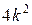является четным числом, так как делится на два без остатка. Квадрат нечетного числа является нечетным числом, поскольку делится на два с остатком.

Теперь мы можем приступать к доказательству иррациональности числа 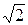. Обозначим: . Если бы 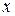было рационально, то можно было бы найти такие два целых числа 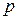и , что 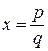, и тогда мы пришли бы к равенству

. (1.1)

Считаем, что дробь несократима, иначе мы с самого начала сократили бы ее на общий наибольший делитель чисел 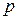и . С правой стороны имеется 2 в качестве множителя, и потому 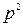есть четное число, и, значит, само 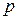также четное. В таком случае можно положить . Тогда равенство (1.1) принимает вид: 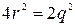, или . Так как с левой стороны теперь имеется 2 в качестве множителя, значит , а следовательно, и – четное. 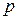Итак, и и – четные числа, т.е. делятся на два, а это противоречит допущению, что дробь несократима.

Итак, равенство (1.1) невозможно, и не может быть рациональным числом.

Иррациональными числами являются также число =3,14… – отношение длины окружности к ее диаметру и неперово число e=2,71… – основание натуральных алгоритмов. Иррациональные числа могут быть представлены бесконечными непериодическими дробями.

и e – это «звезды», одни из самых знаменитых чисел на свете. Ординарных, ничем не примечательных иррациональных чисел гораздо больше. Их общее количество в бесконечное количество раз превышает счетное количество рациональных чисел.

Множество всех рациональных и иррациональных чисел составляет множество действительных чисел (обозначается буквой R). Кантор доказал, что множество всех действительных чиселнесчетно. Другими словами, совокупность всех действительных чисел совершенно иного (так сказать более высокого) «типа бесконечности», чем совокупность одних только целых или одних только рациональных чисел.

Докажем это фактически. Допустим, что все действительные числа, представленные в виде бесконечных десятичных дробей, расположены в порядке последовательности, или списка:

1-е число: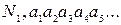

2-е число: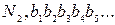

3-е число:

……………………………

где буквы обозначает целую часть, а буквы представляют собой десятичные знаки, стоящие вправо от запятой. Мы допускаем, что эта последовательность дробей охватывает все действительные числа. Существенной частью доказательства является построение с помощью «диагональной процедуры» такого нового числа, относительно которого можно показать, что оно не входит в наш список.

Построим такое число. Для этого возьмем первую цифру после запятой , какую угодно, но отличную от , а также от 0 и 9 (последнее – чтобы избежать затруднений, возникающих из равенств вроде следующего: 0,999…= 1,000…); затем вторую цифру возьмем отличной от , а также от 0 и 9; третью цифру 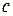– отличной от 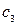и т.д.

Для большей определенности можно условиться в следующем: мы берем 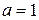, если только 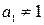, а в случае 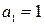возьмем 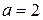; и аналогично для всех прочих цифр Теперь рассмотрим число

Это новое число 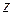наверняка не входит в наш список; действительно, оно не равно первому числу, стоящему в списке, так как от него отличается первой цифрой после запятой, оно не равно второму числу, так как от него отличается второй цифрой после запятой, и вообще отлично от -го числа по списку, так как от него отличается -ой цифрой после запятой. Итак, в нашем списке, составленном будто бы из всех действительных чисел, нет числа 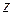. Значит, множество всех действительных чисел несчетно.

Позже всех остальных было открыто множество комплексных чисел, которое обозначается буквой C. Комплексное число записывается следующим образом: , где и – действительные числа, 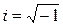– мнимая единица. Множество комплексных чисел равномощно множеству действительных чисел.

Итак, существует, по меньшей мере, два различных «типа бесконечности»: счетная бесконечность натуральных чисел и несчетная бесконечность континуума (от латинского continuum – «непрерывное») действительных (и комплексных) чисел. Дискретная математика имеет дело со счетными множествами. Более того, она, как правило, имеет дело с конечными счетными множествами.