Энтропийная размерность
Пусть X – компактное пространство с метрикой d. Тогда множество 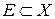 называется r-плотным, если
называется r-плотным, если 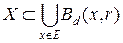 , где
, где  – шар радиуса r относительно метрики d с центром в точке x. Определим r-емкость пространства (X, d) как минимальное число элементов
– шар радиуса r относительно метрики d с центром в точке x. Определим r-емкость пространства (X, d) как минимальное число элементов  в его r-плотном множестве.
в его r-плотном множестве.
Пример 3.1. Например, если X – это отрезок [0, 1] с обычной метрикой, то значение  приближенно равно 1/(2r), потому что необходимо 1/(2r) шаров (т.е. интервалов), чтобы покрыть единичный отрезок.
приближенно равно 1/(2r), потому что необходимо 1/(2r) шаров (т.е. интервалов), чтобы покрыть единичный отрезок.
Пример 3.2. Возьмем единичный квадрат 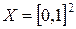 . Тогда значение
. Тогда значение  имеет порядок
имеет порядок  , потому что требуется по крайней мере
, потому что требуется по крайней мере  шаров радиуса r, чтобы покрыть единичный квадрат. Аналогично, для единичного куба значение
шаров радиуса r, чтобы покрыть единичный квадрат. Аналогично, для единичного куба значение  имеет порядок
имеет порядок  .
.
Определение. Если X – вполне ограниченное метрическое пространство, тогда число 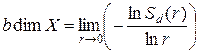 называется энтропийной размерностью пространства X .
называется энтропийной размерностью пространства X .
В англоязычной литературе для энтропийной размерности используют термин «box dimension».
Пример 3.3. Если  , то
, то 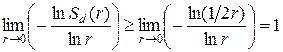 .
.
Если 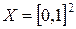 , то
, то 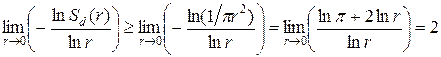 .
.
Если 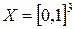 , то
, то
 .
.
Пример 3.4. Найдем энтропийную размерность для менее тривиальных пространств.
1. Троичное канторово множество. Если С – троичное канторово множество, то 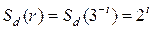 (см. табл. 3.1) и
(см. табл. 3.1) и
 .
.
В табл. 3.1, приведены данные, помогающие понять логику вычисления размерности троичного канторова множества.
Таблица 3.1
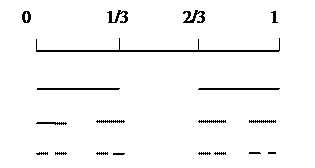
| i | r | 
|
| 1/3 | 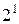
| ||
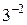
| 
| ||

| 
|
2. Ковер Серпинского. Для квадратного ковра Серпинского S 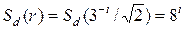 и
и
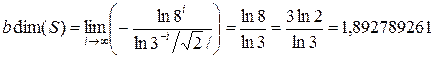 .
.
Для треугольного ковра Серпинского подобным способом получаем, что его энтропийная размерность равна  .
.
3. Снежинка Коха. Для снежинки Коха К мы имеем  , так как ее можно покрыть шарами с центрами на ребрах i-го многоугольника. Таким образом,
, так как ее можно покрыть шарами с центрами на ребрах i-го многоугольника. Таким образом, 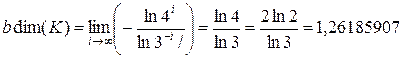 .
.