Булевы функции
Функция 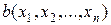 , у которой аргументы пробегают множество {0,1} и которая принимает значение из того же множества {0,1}, называется функцией алгебры логики или булевой функцией.
, у которой аргументы пробегают множество {0,1} и которая принимает значение из того же множества {0,1}, называется функцией алгебры логики или булевой функцией.
Особое значение имеют так называемые элементарные булевы функции. Двухместными элементарными булевыми функциями являются конъюнкция, дизъюнкция, импликация, сумма по модулю 2, эквиваленция, штрих Шеффера и стрелка Пирса. Символы А и B из табл. 4.2 следует в этом случае толковать как булевы переменные {0,1}.
Имеются две одноместные булевы функции, зависящие от x: тождественная функция 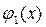 и отрицание
и отрицание 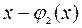 . Это элементарные функции (табл. 4.3).
. Это элементарные функции (табл. 4.3).
Таблица 4.3
| x | 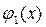
| 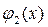
|
Имеются две нуль-местные элементарные булевы функции: это константы 0 и 1. Каждой пропозициональной формуле можно сопоставить булеву функцию. Булева функция 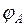 , сопоставленная пропозициональной формуле A, называется функцией истинности формулы A. Любую такую функцию можно описать с помощью соответствующей таблицы истинности (примеры – табл. 4.3, табл. 4.4, табл. 4.5).
, сопоставленная пропозициональной формуле A, называется функцией истинности формулы A. Любую такую функцию можно описать с помощью соответствующей таблицы истинности (примеры – табл. 4.3, табл. 4.4, табл. 4.5).
Пусть 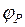 и
и  – функции истинности формул P и Q; пусть {
– функции истинности формул P и Q; пусть {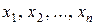 } – множество тех переменных, которые встречаются хотя бы в одной из функций
} – множество тех переменных, которые встречаются хотя бы в одной из функций 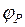 и
и  . Пропозициональные формулы P и Q называются эквивалентными, если на всяком наборе (
. Пропозициональные формулы P и Q называются эквивалентными, если на всяком наборе ( ) значений переменных
) значений переменных 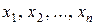 значения функций
значения функций 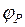 и
и  совпадают (эквивалентность обозначают как: P
совпадают (эквивалентность обозначают как: P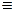 Q).
Q).
Пример 4.3.Покажем эквивалентность выражений
P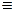 A
A B и Q
B и Q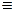
 A
A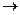 B.
B.
Для этого построим таблицу истинности (табл. 4.4).
Таблица 4.4
| A | B | 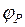 (A, B)
P (A, B)
P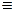 A A B B
|  (A, B)
Q (A, B)
Q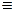  A A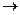 B B
|
Поскольку 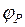 (A, B) =
(A, B) =  (A, B), то P
(A, B), то P 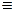 Q.
Q.
Пример 4.4.Покажем эквивалентность выражений
P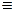 A
A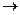 (B
(B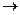 C) и Q
C) и Q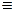 (A
(A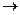 B)
B)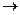 (A
(A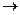 C).
C).
Для этого снова построим таблицу истинности (табл. 4.5).
Таблица 4.5
| A | B | C | 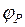 (A, B, C)
P (A, B, C)
P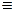 A A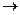 (B (B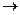 C) C)
|  (A, B, C)
Q (A, B, C)
Q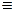 (A (A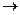 B) B)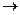 (A (A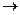 C) C)
|
Поскольку 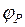 (A, B, C) =
(A, B, C) = (A, B, C), то P
(A, B, C), то P 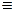 Q. Как можно видеть, в примере 4.3 используются двухместные функции истинности, а в примере 4.4 – трехместные.
Q. Как можно видеть, в примере 4.3 используются двухместные функции истинности, а в примере 4.4 – трехместные.
Основные эквивалентности:

 A
A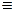 A – правило снятия двойного отрицания;
A – правило снятия двойного отрицания;
A A
A A – идемпотентность конъюнкции;
A – идемпотентность конъюнкции;
A A
A A – идемпотентность дизъюнкции;
A – идемпотентность дизъюнкции;
A*B  B*A – коммутативность связки * (символ * является общим
B*A – коммутативность связки * (символ * является общим
обозначением для связок:  ,
, ,
,  );
);
(A*B)*C  A*(B*C) – ассоциативность связки *;
A*(B*C) – ассоциативность связки *;
A (B
(B C )
C ) (A
(A B)
B) (A
(A C) – дистрибутивность («distributivus» – распределительный) конъюнкции относительно дизъюнкции;
C) – дистрибутивность («distributivus» – распределительный) конъюнкции относительно дизъюнкции;
A ( B
( B C)
C) (A
(A B)
B) (A
(A C) – дистрибутивность дизъюнкции относительно конъюнкции;
C) – дистрибутивность дизъюнкции относительно конъюнкции;
 (A
(A B)
B)
 A
A
 B и
B и  (A
(A B)
B)
 A
A
 B – законы де Моргана;
B – законы де Моргана;
A (A
(A B)
B) A и A
A и A (A
(A B)
B) A – законы поглощения;
A – законы поглощения;
A (
( A
A B)
B) A
A B и A
B и A (
( A
A B)
B) A
A B;
B;
A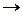 B
B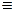
 A
A B;
B;
(A B)
B) (A
(A B)
B) (
( A
A
 B);
B);
A
 A
A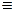 False – закон противоречия;
False – закон противоречия;
A
 A
A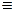 True – закон исключенного третьего;
True – закон исключенного третьего;
A True
True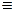 A;
A;
A True
True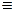 True;
True;
A False
False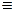 False;
False;
A False
False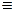 A;
A;