Предикаты
Применяемые в математике высказывания обычно представляют собой описание свойств каких-либо математических объектов или описаний отношений, существующих между этими объектами. Для анализа закономерностей, присущих таким высказываниям, средств алгебры высказываний уже недостаточно. Поэтому вводится понятие предиката.
Индивидная (или предметная) переменная представляет собой знак, обозначающий произвольный индивид из некоторого непустого подмножества множества всех индивидов; это подмножество называется областью изменения данной переменной.
Пусть 
– индивиды из предметной области I. Рассмотрим какое-либо высказывание об этих индивидах и обозначим его через P(
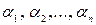). Если n = 1, то P(
) выражает свойство индивида . Если n ³ 2, то данное высказывание описывает некоторое отношение между индивидами (порядок следования индивидов существенен !!!).
Возьмем предметные переменные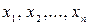 
(с областями изменения 
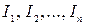соответственно; здесь 
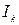– подмножество множества I, 
). Выражение P(
) – и есть предикат. Здесь P может обозначать конкретный предикат (т.е. константу) или переменную-предикат, т.е. предикат в его основном смысле. Предикат, зависящий в точности от n различных предметных переменных, называется n-местным. Высказывание можно рассматривать как нуль-местный предикат, т.е. как предикат, не зависящий от предметных переменных.
Пример 4.5. «x есть четное число» – одноместный предикат; «x есть делитель y» – двуместный (бинарный) предикат.
Пусть P() – предикат, а 
– индивидуальная константа, 
; тогда выражение P(
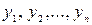) – называется элементарной формулой.
Пример 4.6. Рассмотрим бинарные индивидуальные предикаты: 
, 
и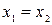 
. Символы >, êи = означают: «больше», «есть делитель», «равно». Выражения 
>3,75 и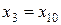 
являются элементарными формулами.
С элементарными формулами можно оперировать так же, как с пропозициональными переменными: к ним применимы все операции алгебры высказываний. При помощи логических связок из элементарных формул строятся новые, предикатные формулы. Сами элементарные формулы тоже считаются предикатными.
Пример 4.7.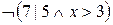 
и 
– предикатные формулы. Их можно «прочитать» следующим образом: первую – «неверно, что 7 – делитель 5 и x больше 3», вторую – «3 не делит 9 или x не равно y».
Использование только элементарных формул и операций алгебры высказываний не дает возможность преодолеть трудности, возникающие, например, при попытке сформировать на формальном логико-математическом языке следующую теорему: «уравнение x+3=8 имеет целочисленное решение». В связи с этим в рассмотрение вводятся кванторы. Используют два квантора: общности (обозначение:
; читается: «для всех...») и существования (обозначение: 
; читается: «существует...»).
Таким образом, предикатные формулы строятся из элементарных формул при помощи логических связок и кванторов всеобщности и существования. Применение кванторов для построения формул осуществляется по следующей схеме. Пусть Н – предикатная формула и x – предметная переменная, которая может и не входит в формулу Н. Тогда выражения (xH) и (xH) считаются предикатными формулами (в этом случае говорят, что Н есть область действия соответствующего квантора x или x).
Приписывание спереди к предикатной формуле какого-либо квантора называется операцией навешивания квантора (или связывания квантором). Конкретное вхождение переменной x в формулу Н называется связанным, если оно либо непосредственно следует за каким-нибудь квантором, либо содержится в области действия некоторого квантора x или x. Если вхождение переменной в формулу не является связанным, то оно называется свободным. Переменная, входящая в формулу Н, называется связанной (свободной), если в Н имеется связанное (свободное) вхождение этой переменной. Таким образом, переменная может быть одновременно и свободной и связанной (в данной формуле).
Пример 4.6. Пусть Z – множество целых чисел. В предикатной формуле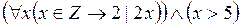 
переменная x является и связанной (три ее вхождения в первый член конъюнкции – связанные), и свободной (вхождение x в формулу x > 5 – свободное). Областью действия квантора x является формула 
В формуле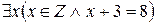 
, представляющей собой истинное высказывание, все три вхождения переменной x – связанные.