Сумма нечетных чисел
Математическая индукция играет огромную роль в дискретной математике (именно в силу ее дискретного характера). Полученные этим методом доказательства в данной области математики почти столь же надежны, как и те, что выведены дедуктивным путем. Начнем с вопроса: «Что мы получим, если просуммируем первые n нечетных чисел?». Непосредственные вычисления дают следующий результат.
1 = 1
1+3 = 4
1+3+5 = 9
1+3+5+7 = 16
1+3+5+7+9 = 25
1+3+5+7+9+11 = 36
1+3+5+7+9+11+13 = 49
1+3+5+7+9+11+13+15 = 64
1+3+5+7+9+11+13+15+17 = 81
1+3+5+7+9+11+13+15+17+19 = 100
Можно заметить, что в каждом случае сумма равна 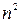 . Так ли будет для всех остальных случаев при любом n? Для доказательства этого необходимо применить метод математической индукции, который заключается в следующем.
. Так ли будет для всех остальных случаев при любом n? Для доказательства этого необходимо применить метод математической индукции, который заключается в следующем.
Допустим, что мы хотим доказать какое-либо свойство для любых положительных целых чисел: 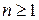 . Также предположим, что мы можем доказать два факта:
. Также предположим, что мы можем доказать два факта:
(а) единица имеет это свойство, и
(б) если n – 1 имеет это свойство, то n также обладает этим свойством. Принцип математической индукции утверждает, что если верны пункты (а) и (б), то каждое натуральное число обладает данным свойством.
Применим этот принцип к рассмотренному выше примеру суммы первых n нечетных чисел. Мы подозреваем, что эта сумма равна 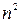 для любого n. То есть:
для любого n. То есть:
1+3+…+ (2n–3) + (2n–1) =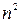 .
.
Единица обладает этим свойством: 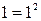 . Допустим, что n–1 также обладает этим свойством. Тогда можем записать:
. Допустим, что n–1 также обладает этим свойством. Тогда можем записать:
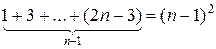 .
.
Добавляя к этой сумме член (2n–1), получим:
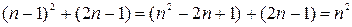 ,
,
что и следовало доказать.