Сумма натуральных чисел
А теперь используем метод индукции для доказательства того, что сумма первых n положительных целых чисел равна 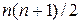 . Если n = 1, то
. Если n = 1, то 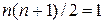 , т.е. единица обладает указанным свойством. Предположим, что сумма первых n – 1 натуральных чисел также обладает этим свойством, т.е. она равна:
, т.е. единица обладает указанным свойством. Предположим, что сумма первых n – 1 натуральных чисел также обладает этим свойством, т.е. она равна: 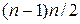 . Прибавив к этой сумме число n, получим:
. Прибавив к этой сумме число n, получим:
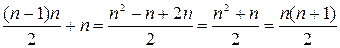 .
.
Таким образом, сумма первых n положительных целых чисел также обладает указанным свойством. Значит, мы можем утверждать, что данная формула справедлива для любого натурального n.
Необходимо заметить, что метод индукции позволяет проверять уже известные формулы, но не позволяет выводить новые формулы. Для получения новых формул приходится напрягать творческие способности. Приведем следующий исторический пример.
Карл Фредерик Гаусс (1777-1855), один из наиболее великих математиков всех времен и народов, учился в начальной школе, когда его учитель задал классу задачу просуммировать все целые числа от 1 до 1000, он рассчитывал на час отдыха, пока его ученики будут заняты делом. Каково же было его удивление, когда Гаусс почти мгновенно получил правильный ответ! Его решение было предельно простым: суммируя первое число с последним, он получил 1 + 1000 = 1001; суммируя второе с предпоследним: 2 + 999 = 1001 и т.д. Всего сумм, равных 1001, получилось пятьсот. Таким образом, ответ равен: 500 · 1001 = 1000 · 1001/2 = 500500.