Размещения с повторением

Если мы выбираем из множества n элементов размещения с повторениями k элементов, то в данном случае k может превосходить n.

Теорема 7.3. Общее число размещений с повторениями k элементов, взятых из совокупности n различных элементов, равно . Доказательство. Задача сводится к заполнению k пустых мест символами n элементов. Каждое место можно заполнить n различными способами, поскольку повторения допускаются. Общее количество размещений будет равно произведению способов заполнения каждого из k пустых мест, то есть: .

Пример 7.4. Максимальное число знаков, которые могут быть представлены с помощью k двоичных символов (k бит), равно числу размещений с повторением из множества, содержащего всего два элемента 0 или 1. Например, если k = 8 (один байт), то =256.

Пример 7.5. Код Бодо (Жан Морис Эмиль Бодо (1845-1903) – французский изобретатель в области телеграфии) использует для кодирования два элементарных сигнала – импульс и паузу, при этом сопоставляемые буквам кодовые слова состоят из пяти таких сигналов. Значит, код Бодо способен передавать = 32 букв. Латинский алфавит содержит 26 букв. С помощью кода Бодо можно также передавать шесть дополнительных знаков, например: знак пропуска между словами, точку, запятую, вопросительный знак, восклицательный знак и двоеточие.

Пример 7.6. Часто по разным соображениям (например, по соображениям безопасности и помехозащищенности) для кодирования сообщений используют не все возможные последовательности в данном алфавите, а только некоторые из них, удовлетворяющие тем или иным ограничениям. Рассмотрим двоичные слова, состоящие из k букв, причем все они имеют фиксированное число t единиц (или, как говорят, слова постоянного веса t). Подсчитаем общее количество таких слов. Каждое из них получится, если мы выберем некоторым образом t позиций из k, и запишем в них единицы, а в остальных k – t позициях – нули. Значит, число всех слов постоянного веса совпадает с числом сочетаний из k элементов по t, т.е. равно

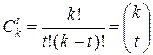. (7.4)