Задача Фибоначчи
Итальянский математик Леонардо Фибоначчи жил в 13 столетии и одним из первых в Европе стал использовать арабские (индийские) цифры. Он придумал несколько искусственную задачу о кроликах, которых выращивают на ферме, причем все они считаются самками, самцы игнорируются. Кролики начинают размножаться после того, как им исполняется два месяца, а потом каждый месяц рожают по кролику. Кролики никогда не умирают.
Нужно определить, сколько кроликов будет на ферме через n месяцев, если в начальный момент времени был только один новорожденный кролик.
Очевидно, что фермер имеет одного кролика в первый месяц и одного кролика – во второй месяц. На третий месяц будет уже два кролика, на четвертый – три и т.д. Обозначим количество кроликов в n месяце как 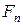 . Таким образом,
. Таким образом,  ,
,  ,
, 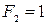 ,
, 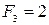 ,
, 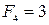 , …
, …
Можно построить алгоритм, позволяющий найти 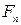 при любом n.
при любом n.
Согласно условию задачи общее количество кроликов 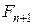 в n+1 месяце раскладывается на три составляющие:
в n+1 месяце раскладывается на три составляющие:
· одномесячные кролики, не способные к размножению, в количестве
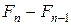 ;
;
· кролики, способные к размножению, в количестве 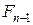 ;
;
· новорожденные кролики, их количество также равно 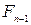 .
.
Таким образом, получим
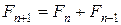 . (8.1)
. (8.1)
Формула (8.1) позволяет вычислить ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …
Числа в данной последовательности называются числами Фибоначчи.
Если принять  и
и  , то с помощью формулы (8.1) можно определить все остальные числа Фибоначчи. Формула (8.1) называется рекуррентной формулой (recurrence – «возвращение» на латыни).
, то с помощью формулы (8.1) можно определить все остальные числа Фибоначчи. Формула (8.1) называется рекуррентной формулой (recurrence – «возвращение» на латыни).
Пример 8.1.Предположим, что имеется лестница в n ступенек. Мы можем подниматься по ней с шагом в одну ступеньку, либо – с шагом в две ступеньки. Сколько существует комбинаций различных способов подъема?
Если n = 1, имеется только один вариант решения задачи. Для n = 2 существует 2 варианта: два единичных шага либо один двойной. Для n = 3 существует 3 варианта: три единичных шага, либо один единичный и один двойной, либо один двойной и один единичный.
В следующем случае n = 4, имеем 5 возможностей (1+1+1+1, 2+1+1, 1+2+1, 1+1+2, 2+2).
Для того чтобы ответить на заданный вопрос при произвольном n, обозначим количество вариантов как 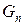 , и попробуем определить
, и попробуем определить 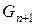 по известным
по известным 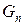 и
и 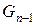 . Если мы стартуем с единичного шага, то имеем
. Если мы стартуем с единичного шага, то имеем 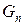 комбинаций для оставшихся n ступенек. Если стартуем с двойного шага, то имеем
комбинаций для оставшихся n ступенек. Если стартуем с двойного шага, то имеем 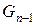 комбинаций для оставшихся n–1 ступенек. Общее количество вариантов для n+1 ступенек равно
комбинаций для оставшихся n–1 ступенек. Общее количество вариантов для n+1 ступенек равно
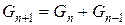 . (8.2)
. (8.2)
Полученная формула как близнец напоминает формулу (8.1). Тем не менее, это не позволяет отождествлять количество комбинаций 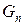 с числами Фибоначчи
с числами Фибоначчи 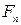 . Мы видим, например, что
. Мы видим, например, что 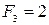 , но
, но 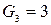 . Однако имеет место следующая зависимость:
. Однако имеет место следующая зависимость:
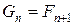 .
.
Это справедливо для n = 1, 2, и также справедливо для каждого n. Числа Фибоначчи и количество комбинаций 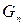 вычисляются по одной и той же формуле, однако начальные значения
вычисляются по одной и той же формуле, однако начальные значения  ,
, 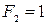 и
и 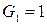 ,
, 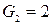 у них различаются.
у них различаются.
Пример 8.2.Этотпример имеет практическое значение для задач помехоустойчивого кодирования. Найдем число всех двоичных слов длины n, не содержащих несколько нулей подряд. Обозначим это число через 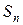 . Очевидно,
. Очевидно, 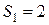 , а слова длины 2, удовлетворяющие нашему ограничению, таковы: 10, 01, 11, т.е.
, а слова длины 2, удовлетворяющие нашему ограничению, таковы: 10, 01, 11, т.е. 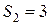 . Пусть
. Пусть 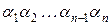 – такое слово из n символов. Если символ
– такое слово из n символов. Если символ 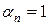 , то
, то 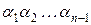 может быть произвольным (
может быть произвольным (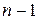 )-буквенным словом, не содержащим несколько нулей подряд. Значит, число слов с единицей на конце равно
)-буквенным словом, не содержащим несколько нулей подряд. Значит, число слов с единицей на конце равно 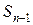 .
.
Если же символ 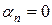 , то обязательно
, то обязательно 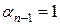 , а первые
, а первые 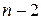 символа
символа 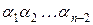 могут быть произвольными с учетом рассматриваемых ограничений. Следовательно, имеется
могут быть произвольными с учетом рассматриваемых ограничений. Следовательно, имеется 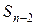 слов длины n с нулем на конце. Таким образом, общее число интересующих нас слов равно
слов длины n с нулем на конце. Таким образом, общее число интересующих нас слов равно
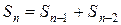 .
.
С учетом того, что 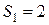 и
и 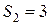 , полученная последовательность чисел – это числа Фибоначчи.
, полученная последовательность чисел – это числа Фибоначчи.
Пример 8.3.В примере 7.6 мы нашли, что число двоичных слов постоянного веса t (и длиной k) равно 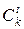 . Теперь найдем число двоичных слов постоянного веса t, не содержащих несколько нулей подряд.
. Теперь найдем число двоичных слов постоянного веса t, не содержащих несколько нулей подряд.
Рассуждать можно так. Пусть 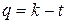 число нулей в рассматриваемых словах. В любом слове имеется
число нулей в рассматриваемых словах. В любом слове имеется 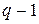 промежутков между ближайшими нулями, в каждом из которых находится одна или несколько единиц. Предполагается, что
промежутков между ближайшими нулями, в каждом из которых находится одна или несколько единиц. Предполагается, что 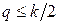 . В противном случае нет ни одного слова без рядом стоящих нулей.
. В противном случае нет ни одного слова без рядом стоящих нулей.
Если из каждого промежутка удалить ровно по одной единице, то получим слово длины 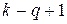 , содержащее
, содержащее  нулей. Любое такое слово может быть получено указанным образом из некоторого (и притом только одного) k-буквенного слова, содержащего
нулей. Любое такое слово может быть получено указанным образом из некоторого (и притом только одного) k-буквенного слова, содержащего  нулей, никакие два из которых не стоят рядом. Значит, искомое число совпадает с числом всех слов длины
нулей, никакие два из которых не стоят рядом. Значит, искомое число совпадает с числом всех слов длины 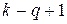 , содержащих ровно
, содержащих ровно  нулей, т.е. равно
нулей, т.е. равно 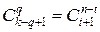 .
.
Пример 8.4.Докажем,что сумма 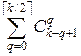 равна числам Фибоначчи для любого целого
равна числам Фибоначчи для любого целого 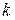 . Символ
. Символ 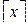 обозначает наименьшее целое число, большее или равное
обозначает наименьшее целое число, большее или равное 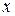 . Например, если
. Например, если 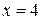 , то
, то 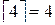 ; а если
; а если 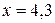 , то
, то 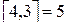 . По-английски эту операцию называют ceil («потолок»). Также встречается символ
. По-английски эту операцию называют ceil («потолок»). Также встречается символ 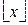 , который обозначает наибольшее целое число, меньшее или равное
, который обозначает наибольшее целое число, меньшее или равное 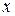 . По-английски эту операцию называют floor («пол»).
. По-английски эту операцию называют floor («пол»).
Если 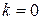 , то
, то 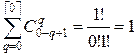 . Если
. Если  , то
, то 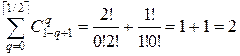 . Если
. Если 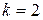 , то
, то 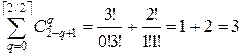 .
.
Таким образом, для рассмотренных случаев сумма действительно равна числам Фибоначчи. Теперь приведем доказательство для общего случая. Поскольку числа Фибоначчи можно получить с помощью рекуррентного уравнения (8.1), то должно выполняться равенство:
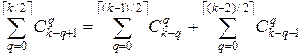 .
.
И оно действительно выполняется:
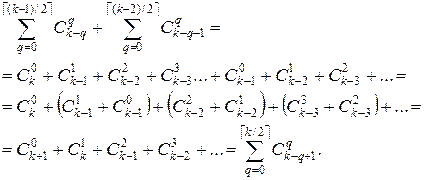
Здесь мы использовали полученную ранее формулу (4.4): 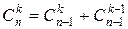 .
.