Формула для чисел Фибоначчи
Теорема 8.1. Числа Фибоначчи можно рассчитать по формуле
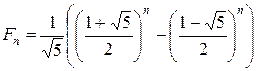 .
.
Доказательство. Убедимся в справедливости этой формулы для n = 0, 1, а затем докажем справедливость данной формулы для произвольного n по индукции. Вычислим отношение двух ближайших чисел Фибоначчи:
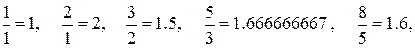
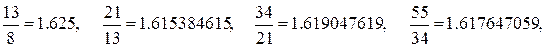
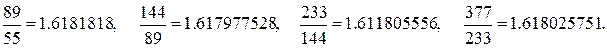
Мы видим, что отношение этих чисел колеблется около значения 1.618 (если игнорировать несколько первых значений). Этим свойством числа Фибоначчи напоминают члены геометрической прогрессии. Примем  , (
, (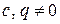 ). Тогда выражение
). Тогда выражение
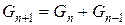
преобразуется в
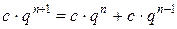 ,
,
которое после упрощений выглядит так
 .
.
Мы получили квадратное уравнение, корни которого равны:

Теперь можем записать:
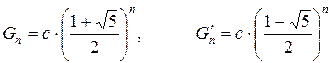
(где c является константой). Оба члена 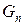 и
и 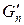 не дают чисел Фибоначчи, например
не дают чисел Фибоначчи, например 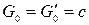 , в то время как
, в то время как  . Однако разность
. Однако разность 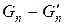 удовлетворяет рекуррентному уравнению:
удовлетворяет рекуррентному уравнению:
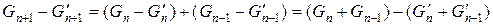 .
.
Для n=0 эта разность дает , то есть:
, то есть: 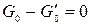 . Однако при n=1 мы имеем
. Однако при n=1 мы имеем 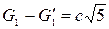 . Чтобы получить
. Чтобы получить  , необходимо принять:
, необходимо принять: 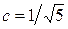 .
.
Теперь мы имеем две последовательности: 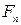 и
и 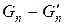 , которые начинаются с одинаковых двух чисел и удовлетворяют одной и той же рекуррентной формуле. Они должны быть равны:
, которые начинаются с одинаковых двух чисел и удовлетворяют одной и той же рекуррентной формуле. Они должны быть равны: 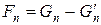 . Теорема доказана.
. Теорема доказана.
При возрастании n член 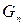 становится очень большим, в то время как
становится очень большим, в то время как 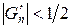 , и роль члена
, и роль члена 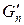 в разности сокращается. Поэтому при больших n приближенно можем записать
в разности сокращается. Поэтому при больших n приближенно можем записать
 .
.
Мы игнорируем 1/2 (поскольку числа Фибоначчи возрастают до бесконечности при росте n до бесконечности).
Отношение 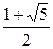 называется золотым сечением, его используют за пределами математики (например, в скульптуре и архитектуре). Золотым сечением является отношение между диагональю и стороной правильного пятиугольника (рис. 8.1).
называется золотым сечением, его используют за пределами математики (например, в скульптуре и архитектуре). Золотым сечением является отношение между диагональю и стороной правильного пятиугольника (рис. 8.1).
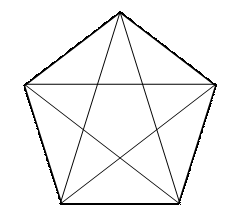
Рис. 8.1. Правильный пятиугольник и его диагонали
Для обозначения золотого сечения принято использовать букву 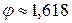 в честь известного афинского скульптора Фидия.
в честь известного афинского скульптора Фидия.