Помехоустойчивое кодирование
Пусть имеется канал связи C, содержащий источник помех:
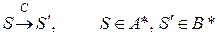 ,
,
где S – множество переданных, а 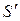 – соответствующее множество принятых по каналу сообщений. Кодирование F, обладающее таким свойством, что
– соответствующее множество принятых по каналу сообщений. Кодирование F, обладающее таким свойством, что
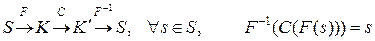 ,
,
называется помехоустойчивым.
Если A=B={0,1}, то ошибки в канале могут быть следующих типов:
· 0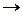 1, 1
1, 1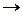 0 – ошибка типа замещения разряда;
0 – ошибка типа замещения разряда;
· 0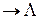 , 1
, 1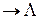 – ошибка типа выпадения разряда;
– ошибка типа выпадения разряда;
·  1,
1,  0 – ошибка типа вставки разряда.
0 – ошибка типа вставки разряда.
Пусть 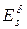 – множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок
– множество слов, которые могут быть получены из слова s в результате всех возможных комбинаций допустимых в канале ошибок 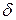 , то есть
, то есть  ,
,  . Если
. Если  , то та конкретная последовательность ошибок, которая позволяет получить из слова s слово
, то та конкретная последовательность ошибок, которая позволяет получить из слова s слово 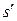 , обозначается
, обозначается  . Если тип возможных ошибок в канале подразумевается, то индекс
. Если тип возможных ошибок в канале подразумевается, то индекс 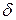 не указывается.
не указывается.
Теорема 9.3. Чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы 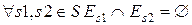 , то есть необходимо и достаточно, чтобы существовало разбиение множества B* на множества
, то есть необходимо и достаточно, чтобы существовало разбиение множества B* на множества 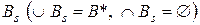 , такое что
, такое что  .
.
Доказательство. Если кодирование помехоустойчивое, то очевидно, что 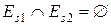 . Обратно: по разбиению
. Обратно: по разбиению  строится функция
строится функция 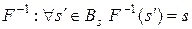 .
.
Рассмотрим множество 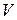 из всех
из всех 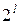 двоичных последовательностей (векторов), имеющих вид
двоичных последовательностей (векторов), имеющих вид
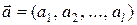 .
.
Введем в множестве 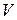 операцию сложения +, определив для последовательностей
операцию сложения +, определив для последовательностей 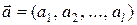 и
и 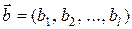 их сумму с помощью соотношения:
их сумму с помощью соотношения:  , где
, где 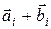 – это сумма по модулю два.
– это сумма по модулю два.
Расстояние Хэмминга 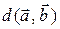 между кодовыми словами определяется как число позиций
между кодовыми словами определяется как число позиций 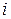 таких, что
таких, что  . При построении вектора
. При построении вектора 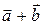 пары одинаковых двоичных символов
пары одинаковых двоичных символов 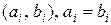 будут давать 0 , а пары различных двоичных символов будут давать 1.
будут давать 0 , а пары различных двоичных символов будут давать 1.
Пример 9.4.(0, 1, 0, 1)+(1, 1, 1, 0)=(1, 0, 1, 1).
Поэтому расстояние Хэмминга 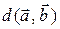 можно определить как число компонент вектора
можно определить как число компонент вектора 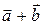 , которые равны 1.
, которые равны 1.
Введенное таким образом расстояние Хэмминга удовлетворяет следующим условиям:
· 
· 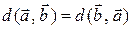 ;
;
· 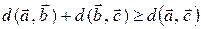 – «неравенство треугольника».
– «неравенство треугольника».
В общем случае расстоянием называют функцию, удовлетворяющую вышеприведенным условиям. Этим условиям, в частности, удовлетворяет геометрическое расстояние между двумя точками (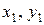 ) и (
) и (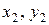 ) на плоскости:
) на плоскости: 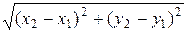 .
.
При наличии 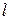 бит можно построить
бит можно построить 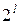 кодовых слов. Однако часто нужны не все из этих слов. Если использовать только часть кодовых слов, то с помощью проверок на четность и других приемов можно обнаружить ошибки и даже их исправлять.
кодовых слов. Однако часто нужны не все из этих слов. Если использовать только часть кодовых слов, то с помощью проверок на четность и других приемов можно обнаружить ошибки и даже их исправлять.
Предположим, что из 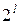 используются только
используются только 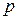 слов:
слов: 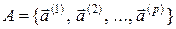 . Если эти слова таковы, что при всех
. Если эти слова таковы, что при всех 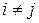 :
:
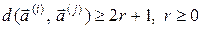 , (7.1)
, (7.1)
то можно исправлять любые ошибки кратности  .
.
Допустим, что в некоторых  компонентах слова при передаче возникли ошибки, в результате которых символы 0 были приняты как 1, а символы 1 – как 0 (ошибки типа замещения). Получившееся в результате слово
компонентах слова при передаче возникли ошибки, в результате которых символы 0 были приняты как 1, а символы 1 – как 0 (ошибки типа замещения). Получившееся в результате слово 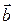 находится на расстоянии
находится на расстоянии  от слова
от слова 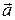 . Следовательно, если считать, что ошибки при передаче могут возникать не более чем в
. Следовательно, если считать, что ошибки при передаче могут возникать не более чем в  компонентах, то совокупность всех слов, которые могут получиться из
компонентах, то совокупность всех слов, которые могут получиться из 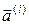 , представляет собой множество
, представляет собой множество 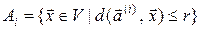 .
.
Из неравенства треугольника и условия (7.1) следует 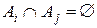 , если только
, если только 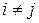 . Действительно, допустим, что существует слово
. Действительно, допустим, что существует слово  . Тогда
. Тогда 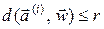 и
и 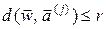 .
.
Согласно неравенству треугольника
 ,
,
что приводит к противоречию с условием (9.1).
Множество 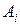 называется областью декодирования для слова
называется областью декодирования для слова 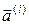 . Так как области декодирования не пересекаются, то при приеме слова из области декодирования
. Так как области декодирования не пересекаются, то при приеме слова из области декодирования 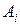 можно считать, что передавалось слово
можно считать, что передавалось слово 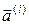 . Если при этом число ошибок не превосходит
. Если при этом число ошибок не превосходит  , то при приеме всегда будет приниматься правильное решение.
, то при приеме всегда будет приниматься правильное решение.
Так как число элементов 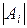 в множестве
в множестве 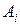 равно числу способов выбора некоторых
равно числу способов выбора некоторых 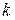 (
( ) компонент слова
) компонент слова 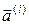 , то
, то
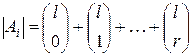 .
.
Далее, так как 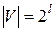 , то:
, то: 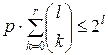 , то есть
, то есть
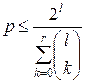 . (9.2)
. (9.2)
Неравенство (9.2) называется границей Хэмминга. Оно дает оценку сверху для числа 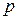 кодовых слов, которые можно использовать для передачи, если их длина равна
кодовых слов, которые можно использовать для передачи, если их длина равна 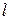 бит и нужно исправлять все
бит и нужно исправлять все  -кратные ошибки.
-кратные ошибки.
Пример 9.5.Пусть 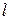 =8, тогда
=8, тогда 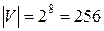 . Поскольку
. Поскольку 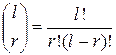 , то
, то 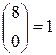 ;
;  ;
; 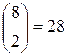 ;
; 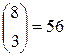 ;
; 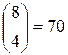 .
.
Если  =4, то
=4, то  .
.
Если  =3, то
=3, то 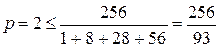 .
.
Если  =2, то
=2, то 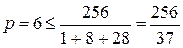 .
.
Если  =1, то
=1, то  .
.
Если  =0, то
=0, то  .
.
Таким образом, если встречаются только одиночные ошибки типа замещения, то при использовании 8 бит можно безошибочно передавать 28 слов. В общем случае, если имеется 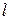 бит и нужно исправлять одиночные ошибки типа замещения, то граница Хэмминга определяется следующим выражением, являющимся частным случаем формулы (9.2):
бит и нужно исправлять одиночные ошибки типа замещения, то граница Хэмминга определяется следующим выражением, являющимся частным случаем формулы (9.2):
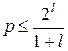 . (9.3)
. (9.3)
Обозначим минимальное число бит, необходимое для передачи 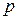 слов, буквой
слов, буквой 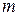 . Тогда:
. Тогда: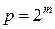 , и из формулы (9.3) следует
, и из формулы (9.3) следует
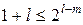 . (9.4)
. (9.4)
Таким образом, для помехоустойчивого кодирования сигналов при одиночных ошибках типа замещения необходимо использовать дополнительные 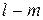 бит, количество которых должно удовлетворять условию (9.4). Рассматриваемый случай простейший, но одновременно практически очень важный. Таким свойством, как правило, обладают внутренние шины передачи данных в современных компьютерах.
бит, количество которых должно удовлетворять условию (9.4). Рассматриваемый случай простейший, но одновременно практически очень важный. Таким свойством, как правило, обладают внутренние шины передачи данных в современных компьютерах.
Пример 9.6.Для сообщения длиной 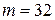 потребуется
потребуется 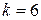 дополнительных разрядов, поскольку 64=
дополнительных разрядов, поскольку 64=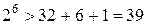 .
.
Код, в котором используются дополнительные разряды для помехоустойчивой передачи сигналов, называется кодом Хэмминга.