Модулярная арифметика
В этом разделе все числа – целые. Говорят, что число a сравнимо по модулю n с числом b (обозначение 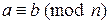 ), если a и b при делении на n дают один и тот же остаток:
), если a и b при делении на n дают один и тот же остаток:
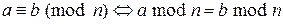 .
.
Отношение сравнимости рефлексивно, симметрично и транзитивно и является отношением эквивалентности. Классы эквивалентности по отношению сравнимости (по модулю n) называются вычетами (по модулю n). Множество вычетов по модулю n обозначается  . Обычно из каждого вычета выбирают одного представителя – неотрицательное число, которое при делении на n дает частное 0. Это позволяет считать, что
. Обычно из каждого вычета выбирают одного представителя – неотрицательное число, которое при делении на n дает частное 0. Это позволяет считать, что 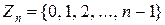 , и упростить обозначения.
, и упростить обозначения.
Над вычетами (по модулю n) определены операции сложения и умножения по модулю n, обозначаемые соответственно  и
и  , и определяемые следующим образом:
, и определяемые следующим образом:
 ,
, 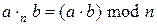 .
.
Если из контекста ясно, что подразумевается операция по модулю n, то индекс n опускается.
Рассмотрим 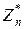 – подмножество
– подмножество  чисел, взаимно простых с n. Числа называются взаимно простыми, если их наибольший общий делитель равен единице. Для чисел из множества
чисел, взаимно простых с n. Числа называются взаимно простыми, если их наибольший общий делитель равен единице. Для чисел из множества 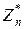 существуют обратные числа по отношению к операции умножения по модулю n.
существуют обратные числа по отношению к операции умножения по модулю n.