Канторово множество
Математика изобилует парадоксальными объектами. Одним из них является канторово множество. Оно описывается следующим образом. Рассмотрим единичный отрезок, показанный на рис. 3.1. Удалим из него открытую среднюю часть (1/3, 2/3) оставив два отрезка длины 1/3. Затем применим ту же самую процедуру к этим отрезкам, т.е. удалим их средние части. Продолжая процесс индуктивно до бесконечности, получим троичное канторово множество.
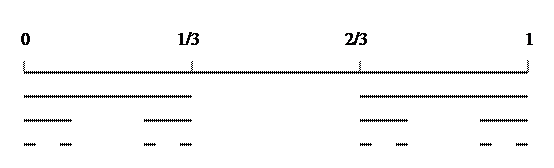
Рис. 3.1. Троичное канторово множество
Канторово множество можно построить не только геометрически, но и аналитически. Оно является совокупностью таких чисел из отрезка [0, 1], которые могут быть записаны в троичной системе счисления без использования цифры 1.
Доказательство. Интервал (1/3, 2/3) – это в точности множество чисел, у которых в первом разряде после запятой стоит 1 (при записи в троичной системе), т.е. которые в троичной системе не могут быть записаны в виде 0,0… или 0,2… (заметим, что 1/3 можно записать как 0,02222…, а 2/3 как 0,20000…). Соответственно средние части оставшихся отрезков – в точности те числа, для которых второй разряд после запятой должен быть равен 1, и т.д.
Троичное канторово множество обладает удивительными свойствами. Оно вполне несвязно, однако одновременно оно несчетно.
Доказательство. Сопоставляя каждой точке 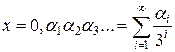 , (
, (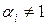 ) число
) число 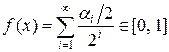 , мы определяем отображение (функцию), потому что все двоичные разложения можно представить в таком виде. Образ канторова множества несчетен, следовательно, и само это множество несчетно. Функция
, мы определяем отображение (функцию), потому что все двоичные разложения можно представить в таком виде. Образ канторова множества несчетен, следовательно, и само это множество несчетно. Функция  представлена на рис. 3.1. Она называется канторовой лестницей.
представлена на рис. 3.1. Она называется канторовой лестницей.

Рис. 3.2. Канторова лестница
В англоязычной литературе канторову лестницу называют «лестницей дьявола» (devil stairs). Этот термин возник из-за необычной ситуации – график этой функции полностью состоит из «ступенек», а именно горизонтальных отрезков на дополнительных интервалах, но все же разрывов эта функция не имеет – она непрерывна. Таким образом, сами ступеньки на лестнице имеются, но вот их боковые грани отсутствуют. Тем самым мы получаем удивительный пример функции с некоторыми экзотическими свойствами. Микроскопическая структура канторовой лестницы точно такая же, как и глобальная структура; она не станет более простой в любом другом уменьшенном масштабе. Линии, обладающие подобными свойствами, называются фракталами. Представленный на рис. 3.1 график канторовой лестницы был построен с использованием следующей программы MATLAB.
for k=1:1023
Sum=0;
for i=1:10
p=floor(k/(2^(10-i)));
if rem(p,2)==0
b(i)=0;