рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Доказательство теоремы о свертке.

Реферат Курсовая Конспект

Выберите учебное заведение

Доказательство теоремы о свертке.

Доказательство теоремы о свертке. - раздел Математика, Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ...

Пример 9.5.Применяя теорему о свертке, найти оригинал изображения:

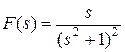Решение. Имеем ,

, .

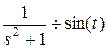Поэтому .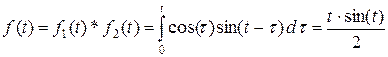

Теорема 9.8. (первая теорема разложения).

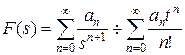. (9.21)

Доказательство. Формула (9.21) прямо следует из формулы (9.20).

Пример 9.6.Найти оригинал изображения.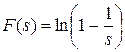

Решение. Известно, что логарифмическая функция может быть разложена в следующий степенной ряд:

В соответствии с первой теоремой разложения получаем:

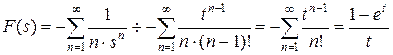Теорема 9.9. (вторая теорема разложения).

Если – рациональная правильная несократимая дробь, а 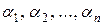– простые (не кратные) корни уравнения: , то

, (9.21)

где , .

Доказательство. Прежде всего, заметим, что требование правильности дроби в данной теореме обязательно, так как эта дробь – изображение, и должно быть выполнено условие .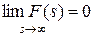

Далее известно, что в случае простых корней знаменателя правильная рациональная дробь может быть разложена на простейшие следующим образом:

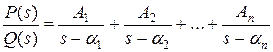Для нахождения коэффициента 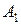умножим обе части равенства на ():

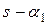Введем обозначение 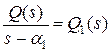, тогда предыдущее равенство можно записать в виде:

Полагая 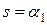, найдем 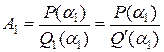. Подобно этому вычисляются и остальные коэффициенты разложения. Используя теорему смещения, приходим к формуле (9.21).

Пример 9.7.Найти оригинал для изображения.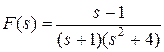

Решение: – правильная рациональная несократимая дробь, причем

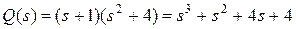Корни знаменателя: .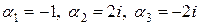

, , .

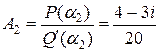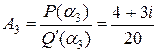Здесь мы применили формулу Эйлера: .

Пример 9.8.Решить дифференциальное уравнение

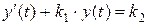
при начальном условии: , 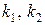– константы.

Решение: Для решения используем операционное исчисление. Уравнение в изображениях

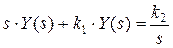Решая его относительно , получим . Применим вторую теорему разложения.

; ; .

; .

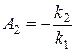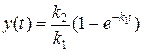Пример 9.9.Решить дифференциальное уравнение

при начальных условиях: , .

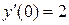Решение: Уравнение в изображениях

Подставляем начальные условия:

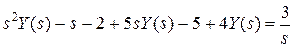Решаем полученное уравнение как обычное алгебраическое

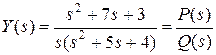Совершаем обратное преобразование по формуле:

; ;

, .

; , .

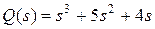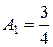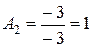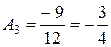Пример 9.10.Вычислить интеграл

Найдем изображение этого интеграла

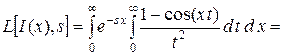
Отсюда следует: .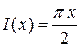

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Введение... Обыкновенные дифференциальные уравнения ОДУ не относятся к области дискретной математики Мы рассмотрим этот тип...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Доказательство теоремы о свертке.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Операционное исчисление
Существуют различные способы решения дифференциальных уравнений. В данном разделе мы ознакомимся со способом, использующим операционное исчисление. Этот способ применяется к

Преобразование Лапласа
Хевисайд не дал строгого математического обоснования своего метода. Это было сделано позже с помощью интегрального преобразования Лапласа. В результате такого преобразования функция

Свойства изображений
· Если два изображения и

Изображения некоторых функций
1. Функция Хевисайда :

Основные теоремы операционного исчисления
В большинстве случаев применение операционного исчисления к решению задач укладывается в следующую схему. Пусть требуется найти некоторый результат в виде функции

Доказательство.
. Теорема 9.7. (о свертке). Если

Производящая функция
Степенной ряд , коэффициентами которого являются элементы последовательности

Решение однородного рекуррентного уравнения
Однородное рекуррентное уравнение получается при j (n) = 0. Метод решения является обобщением решения предыдущего примера. Вначале производящая функция находится как рациональная функ

Метод решения неоднородного рекуррентного уравнения
Рассмотрим неоднородное линейное рекуррентное уравнение , n = 0, 1, 2, …, коэффи

Дискретное преобразование Лапласа
Дискретное преобразование Лапласа применяют к так называемым решетчатым функциям. Решетчатой функцией

Основные теоремы дискретного преобразования Лапласа
1. Свойство линейности: . 2. Теорема сдвига:

Z-преобразование
Если ввести обозначение , то теорема сдвига примет следующую форму

Дискретная интерпретация операционного исчисления Микусиньского
Как известно, операционное исчисление, позволяющее сводить дифференциальные задачи к алгебраическим, возникло благодаря работам английского ученого Оливера Хевисайда (1859-1925), который предложил

Доказательство.
Все элементы матрицы равны нулю, за исключением одного. Это элемент в нижнем левом углу, который равен ед

Теоремы дискретного операционного исчисления
Теоремам непрерывного операционного исчисления можно поставить в соответствие теоремы дискретного операционного исчисления. Приведем несколько таких теорем. Теорема 11.7.

Теорема 11.8.
, (). (11.2

Теорема 11.9.
, (). (11.2

Применение дискретного операционного исчисления
Преимуществом дискретного операционного исчисления является то, что его можно использовать как численный метод, а не только как символьные преобразования. При этом оно опирается на хорошо отработан

Plot(Out), hold on
Рис. 11.2 Как можно видеть, для решения задачи достат