рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Решение однородного рекуррентного уравнения
Реферат Курсовая Конспект
Решение однородного рекуррентного уравнения
Решение однородного рекуррентного уравнения - раздел Математика, Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Однородное Рекуррентное Уравнение Получается При J (N) = 0. Мет...
Однородное рекуррентное уравнение получается при j (n) = 0. Метод решения является обобщением решения предыдущего примера. Вначале производящая функция находится как рациональная функция, которая далее представляется в виде суммы частичных дробей и разлагается в степенной ряд. Предположим, что последовательность чисел  удовлетворяет следующему однородному линейному рекуррентному уравнению
удовлетворяет следующему однородному линейному рекуррентному уравнению
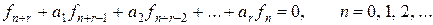 .
.
где 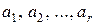 – заданные числа и
– заданные числа и  .
.
Для задания начальных условий фиксируем значения  . Обозначим через F(z) производящую функцию последовательности
. Обозначим через F(z) производящую функцию последовательности 
По заданным постоянным коэффициентам уравнения построим многочлен
 .
.
Этот многочлен можно рассматривать как производящую функцию последовательности:  . Коэффициент
. Коэффициент 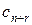 при
при 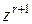 и r > 0 в произведении производящих функций
и r > 0 в произведении производящих функций 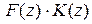 , определяется соотношением
, определяется соотношением

Он равен нулю, поскольку рекуррентное уравнение однородное. Это означает, что многочлен
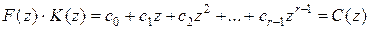
имеет степень самое большее (r–1), и, следовательно, степень числителя рациональной функции F(z) = C(z) / K(z) меньше степени знаменателя.
Характеристическим многочленом линейного однородного рекуррентного уравнения называется многочлен:
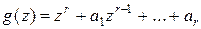 ,
,
имеющий степень “r”; корни этого многочлена называются характеристическими. Если различные характеристические корни (среди которых могут быть мнимые) обозначить через  , а их кратности обозначить через
, а их кратности обозначить через  , то можно записать следующие равенства:
, то можно записать следующие равенства:
 ,
,
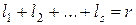 .
.
Характеристический многочлен 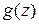 и многочлен K(z) связаны между собой соотношениями
и многочлен K(z) связаны между собой соотношениями
 .
.
Отсюда следует, что
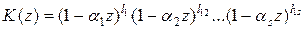 .
.
Используя это, можно записать
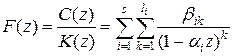 ,
,
где  – неопределённый коэффициент.
– неопределённый коэффициент.
Каждая дробь этой суммы имеет вид  , поэтому её можно разложить в степенной ряд следующего вида:
, поэтому её можно разложить в степенной ряд следующего вида:
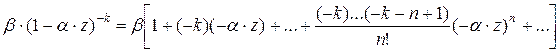 .
.
Коэффициент при  в этом ряде равен
в этом ряде равен
 .
.
Если заметить, что биномиальный коэффициент
 ,
,
входящий в последнее равенство, является многочленом степени 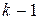 по
по 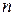 , то легко проверить, что
, то легко проверить, что
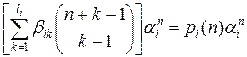 ,
,
где  – многочлен от
– многочлен от 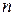 степени самое большее
степени самое большее  . Следовательно
. Следовательно

и  – является общим решением однородного линейного рекуррентного уравнения.
– является общим решением однородного линейного рекуррентного уравнения.
Пример 10.3. С помощью общего метода найти общий член последовательности чисел Фибоначчи.
Решение: Уравнение 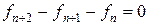 имеет характеристический многочлен
имеет характеристический многочлен  , где
, где  ;
;  . В этом случае
. В этом случае  и
и 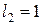 и, следовательно,
и, следовательно, 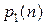 и
и 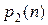 – многочлены степени 0 от n, т.е. постоянные. Поэтому
– многочлены степени 0 от n, т.е. постоянные. Поэтому 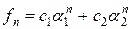 , где
, где 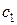 и
и 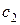 – неопределённые постоянные. Так как
– неопределённые постоянные. Так как 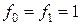 , то, подставляя n = 0, 1, получаем
, то, подставляя n = 0, 1, получаем  ;
; 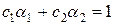 . Решая эти уравнения, находим
. Решая эти уравнения, находим
 ;
; 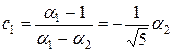 .
.
Отсюда следует:  .
.
Решение этого упражнения показывает, что если все характеристические корни 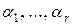 являются простыми, то общее решение однородного уравнения имеет вид:
являются простыми, то общее решение однородного уравнения имеет вид:  , где
, где 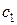 ,
, 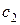 , …,
, …,  – это «r» неопределённых постоянных. Для определения этих постоянных используются r начальных условий, а именно значения
– это «r» неопределённых постоянных. Для определения этих постоянных используются r начальных условий, а именно значения 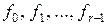 . Если
. Если 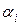 является корнем кратности
является корнем кратности  , то
, то  представляет собой многочлен степени
представляет собой многочлен степени  :
:
 ,
,
где 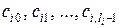 –
–  неопределённых постоянных. Начальные условия однозначно определяют все «r» неопределённых постоянных.
неопределённых постоянных. Начальные условия однозначно определяют все «r» неопределённых постоянных.
Пример 10.4.Найти решение уравнения  c начальными условиями
c начальными условиями  ,
, 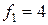 .
.
Решение: Так как характеристический многочлен  имеет корень z = 2 кратности 2, то
имеет корень z = 2 кратности 2, то  . С помощью начальных условий находим:
. С помощью начальных условий находим:
 ;
;  ;
;  .
.
Таким образом, решение рассматриваемого уравнения:
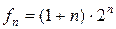 .
.
– Конец работы –
Эта тема принадлежит разделу:
Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Введение... Обыкновенные дифференциальные уравнения ОДУ не относятся к области дискретной математики Мы рассмотрим этот тип...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение однородного рекуррентного уравнения
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов