рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- II. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.
Реферат Курсовая Конспект
II. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.
II. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. - раздел Математика, МАТРИЦЫ И ИХ ВИДЫ Введение. Аналитическая Геом...
Введение.
Аналитическая геометрия как наука занимается изучением свойств геометрических объектов средствами алгебры. Основным методом этой науки является метод координат, позволяющий определять положение точки в некотором пространстве с помощью чисел-координат этой точки.
Так как в геометрии ее объекты (линии, поверхности, фигуры) определяются как множества точек, обладающих некоторым общим геометрическим свойством, то метод координат позволил описывать эти объекты, используя связи между числами – координатами точек объектов, т.е. средствами алгебры.
1. Плоская линия и ее уравнение в 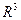 .
.
В геометрии плоская линия  определяется как множество точек плоскости (геометрическое место точек), обладающих некоторым общим для всех точек линии свойством. Например, окружность радиуса
определяется как множество точек плоскости (геометрическое место точек), обладающих некоторым общим для всех точек линии свойством. Например, окружность радиуса  есть множество всех точек плоскости, удаленных на расстояние
есть множество всех точек плоскости, удаленных на расстояние  от некоторой точки
от некоторой точки 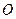 этой плоскости.
этой плоскости.
Введем аналитическое определение плоской линии. Пусть на плоскости введена декартова система координат. Выберем на этой плоскости произвольную точку 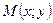 . Рассмотрим вместе со множеством точек координатной плоскости множество уравнений вида
. Рассмотрим вместе со множеством точек координатной плоскости множество уравнений вида 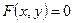 . Будем говорить, что числа
. Будем говорить, что числа  удовлетворяют уравнению
удовлетворяют уравнению 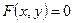 , если
, если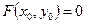 , и ему не удовлетворяют, если
, и ему не удовлетворяют, если 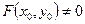 . Например, числа
. Например, числа 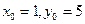 удовлетворяют уравнению
удовлетворяют уравнению 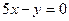 и не удовлетворяют уравнению
и не удовлетворяют уравнению 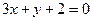 .
.
ОПРЕДЕЛЕНИЕ 1.1. Уравнение 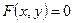 , связывающие между собой переменные
, связывающие между собой переменные  и
и 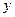 , называют уравнением плоской линии
, называют уравнением плоской линии  в выбранной системе координат, если координаты
в выбранной системе координат, если координаты  и
и 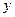 любой точки
любой точки  этой линии ему удовлетворяют, а координаты всех точек, не лежащих на ней, ему не удовлетворяют.
этой линии ему удовлетворяют, а координаты всех точек, не лежащих на ней, ему не удовлетворяют.
Множество всех точек координатной плоскости, координаты которых удовлетворяют уравнению 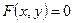 , будем называть плоской линией (плоской кривой).
, будем называть плоской линией (плоской кривой).
Заметим, что множество точек может содержать сколько угодно точек быть конечным или даже оказаться пустым. Например, уравнению 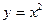 удовлетворяют координаты бесконечного множества точек; уравнению
удовлетворяют координаты бесконечного множества точек; уравнению  удовлетворяют координаты только одной точки
удовлетворяют координаты только одной точки 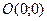 ; уравнению
; уравнению 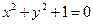 не удовлетворяют координаты всех точек плоскости. В первом случае плоская кривая является обычной кривой (парабола); во втором – кривая представляет собой точку; в третьем – мнимую плоскую кривую (мнимая окружность).
не удовлетворяют координаты всех точек плоскости. В первом случае плоская кривая является обычной кривой (парабола); во втором – кривая представляет собой точку; в третьем – мнимую плоскую кривую (мнимая окружность).
Из определения 1.1 следует, что любое уравнение вида 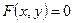 и общем случае определяет на координатной плоскости
и общем случае определяет на координатной плоскости  некоторую линию. Для ее построения можно воспользоваться обычным методом точек.
некоторую линию. Для ее построения можно воспользоваться обычным методом точек.
ПРИМЕР 1.1. Построить линию, заданную уравнением 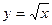 .
.
Придавая переменной  различные числовые значения и вычисляя соответствующие значения
различные числовые значения и вычисляя соответствующие значения 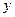 , построим таблицу:
, построим таблицу:
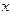
| … | ||||
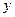
| … |
Введем на плоскости декартову систему координат и построим на этой плоскости соответствующие точки с координатами  ,
, 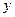 . Соединяя построенные точки линией, получим искомую кривую (рис.1).
. Соединяя построенные точки линией, получим искомую кривую (рис.1).

В аналитической геометрии из бесконечного множества уравнений наиболее полно изучаются так называемые алгебраические уравнения.
ОПРЕДЕЛЕНИЕ 1.2. Уравнение 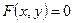 называется алгебраическим, если выражение
называется алгебраическим, если выражение 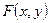 есть сумма конечного числа слагаемых вида
есть сумма конечного числа слагаемых вида 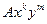 , где
, где 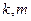 - целые неотрицательные числа,
- целые неотрицательные числа, 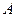 - действительное число. При этом наибольшая из сумм степеней
- действительное число. При этом наибольшая из сумм степеней 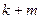 называется степенью уравнения.
называется степенью уравнения.
Например, уравнения 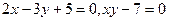 есть алгебраические уравнения соответственно первой и второй степеней. Уравнение
есть алгебраические уравнения соответственно первой и второй степеней. Уравнение 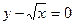 алгебраическим не является.
алгебраическим не является.
Уравнение 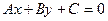 , где
, где 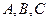 - действительные числа, является наиболее общим алгебраическим уравнением первой степени. Уравнение
- действительные числа, является наиболее общим алгебраическим уравнением первой степени. Уравнение 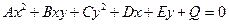 - общее алгебраическое уравнение второй степени.
- общее алгебраическое уравнение второй степени.
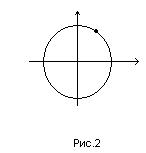
Задача изучения свойств линии по известному ее уравнению является одной из главных задачи аналитической геометрии. Второй центральной задачей этой науки является решение обратной задачи, т.е. задачи определения уравнения линии, если известны все ее точки. Например, непосредственно из определения окружности с центром в начале координат (рис.2) следует, что 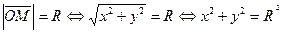 , если произвольная точка плоскости
, если произвольная точка плоскости 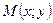 принадлежит окружности, и
принадлежит окружности, и 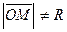 , если точка
, если точка 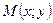 не принадлежит окружности. Следовательно,
не принадлежит окружности. Следовательно, 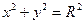 , если
, если  или
или  , если
, если  . Тогда, согласно определению 1.1, уравнение
. Тогда, согласно определению 1.1, уравнение 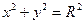 есть уравнение искомой окружности.
есть уравнение искомой окружности.



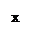
2. Прямая линия на плоскости. Уравнение прямой по точке и нормальному вектору.
Положение прямой  на координатной плоскости
на координатной плоскости  вполне определяется заданием:
вполне определяется заданием:
1) любых двух точек;
2) точки и вектора, параллельного  ;
;
3) точки и вектора, перпендикулярного  ;
;
4) углового коэффициента и отрезка, отсекаемого прямой от оси 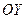 ;
;
5) других величин.
Поставим задачу определения уравнения прямой  в каждом из перечисленных способов ее задания.
в каждом из перечисленных способов ее задания.
3. Уравнение прямой по точке и нормальному вектору.
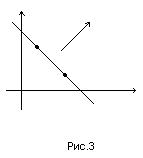
Пусть на плоскости  дана точка
дана точка  и вектор
и вектор  (рис.3). Требуется определить уравнение прямой
(рис.3). Требуется определить уравнение прямой  , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  (вектор
(вектор  ^
^ называется нормальным вектором прямой).
называется нормальным вектором прямой).
 Выберем на плоскости произвольную точку
Выберем на плоскости произвольную точку 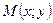 и построим вектор
и построим вектор 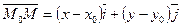 .
.



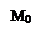
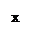
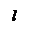

Рассмотрим два случая:
1) пусть точка  . Тогда
. Тогда 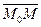 ^
^ Þ
Þ или
или
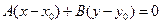 ; (1)
; (1)
2) если точка 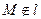 , то векторы
, то векторы 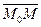 и
и  не перпендикулярны. Следовательно,
не перпендикулярны. Следовательно,  или
или  . Из 1) и 2) и определения 1.1 уравнения плоской линии следует, что уравнение (1) является уравнением искомой прямой
. Из 1) и 2) и определения 1.1 уравнения плоской линии следует, что уравнение (1) является уравнением искомой прямой  .
.
Уравнение (1) называется уравнением прямой по точке и нормальному вектору 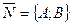 .
.
ПРИМЕР2.1. Найти уравнение прямой  , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 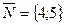 .
.
Решение. Уравнение прямой  будем искать в виде
будем искать в виде 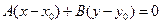 . По условию
. По условию 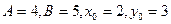 . Тогда для
. Тогда для  получим
получим 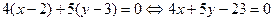 .
.
4. Уравнение прямой по точке и направляющему вектору.
Пусть на плоскости  дана точка
дана точка  и вектор
и вектор  (рис.4).
(рис.4).

| |||
| |||


|


Требуется определить уравнение прямой  , проходящей через точку
, проходящей через точку  параллельно вектору
параллельно вектору  (вектор
(вектор  ïï
ïï называется направляющим вектором прямой).
называется направляющим вектором прямой).
Выберем на плоскости  произвольную точку
произвольную точку 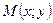 и построим вектор
и построим вектор  .
.
Рассмотрим два случая:
1) пусть точка  . Тогда
. Тогда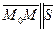 . Следовательно, векторы
. Следовательно, векторы 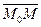 и
и  коллинеарны. Итак,
коллинеарны. Итак, 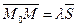 , где
, где  -некоторое действительной число. Тогда
-некоторое действительной число. Тогда 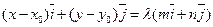 Û
Û
 ; (2)
; (2)
2) пусть точка 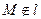 . Тогда
. Тогда 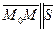 Û
Û  ни при каком
ни при каком  . Отсюда и
. Отсюда и 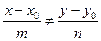 . Из 1) и 2) и определения 1.1 уравнения линии следует, что уравнение (2) является уравнением искомой прямой
. Из 1) и 2) и определения 1.1 уравнения линии следует, что уравнение (2) является уравнением искомой прямой  . Уравнение (2) называется уравнением прямой по точке и направляющему вектору
. Уравнение (2) называется уравнением прямой по точке и направляющему вектору 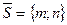 . Его также называют уравнением прямой.
. Его также называют уравнением прямой.
Замечание. Если прямая  проходит через точку
проходит через точку  и параллельна оси
и параллельна оси 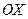 , то направляющий вектор
, то направляющий вектор  также параллелен этой оси. Следовательно,
также параллелен этой оси. Следовательно,  . Хотя его проекция
. Хотя его проекция 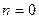 , уравнение этой прямой условились записывать в канонической форме, т.е.
, уравнение этой прямой условились записывать в канонической форме, т.е.  . Последнее уравнение считается другой формой записи уравнения этой прямой
. Последнее уравнение считается другой формой записи уравнения этой прямой  . Аналогично каноническое уравнение вида
. Аналогично каноническое уравнение вида  означает другую форму записи уравнения прямой
означает другую форму записи уравнения прямой 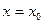 , проходящей через точку
, проходящей через точку  параллельно оси
параллельно оси 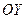 .
.
– Конец работы –
Эта тема принадлежит разделу:
МАТРИЦЫ И ИХ ВИДЫ
ОПЕРАЦИИ НАД МАТРИЦАМИ... Равенство матриц... Две матрицы А и В называются равными А В если они имеют одинаковые размеры и их соответствующие элементы равны...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: II. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов