рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Уравнение прямой по двум точкам.
Реферат Курсовая Конспект
Уравнение прямой по двум точкам.
Уравнение прямой по двум точкам. - раздел Математика, МАТРИЦЫ И ИХ ВИДЫ Пусть На Плоскости ...
Пусть на плоскости  даны две точки
даны две точки 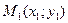 ,
, 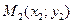 и требуется найти уравнение прямой
и требуется найти уравнение прямой  , проходящей через эти точки (рис.5). Согласно формуле (2) уравнение любой прямой, проходящей через точку
, проходящей через эти точки (рис.5). Согласно формуле (2) уравнение любой прямой, проходящей через точку 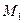 , запишется в виде
, запишется в виде
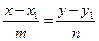 , (3)
, (3)
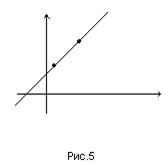
где 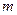 и
и  - проекции неизвестного направляющего вектора
- проекции неизвестного направляющего вектора  этой прямой.
этой прямой.
|
| ||||
 | |||
|
Примем за направляющий вектор  вектор
вектор  . Тогда
. Тогда  ,
, 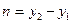 . Подставляя найденные числа в уравнение (3), получим уравнение искомой прямой
. Подставляя найденные числа в уравнение (3), получим уравнение искомой прямой  .
.
 . (4)
. (4)
Уравнение (4) называется уравнением прямой, проходящий через две данные точки.
ПРИМЕР 4.1. Найти уравнение прямой, проходящей через точки 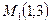 и
и  .
.
Решение. Полагая в (4) 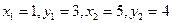 , получим искомое уравнение
, получим искомое уравнение 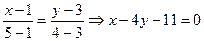 .
.
6. Уравнение прямой по точке и угловому коэффициенту.
Пусть на плоскости  проведена некоторая прямая
проведена некоторая прямая  (рис.6). Углом наклона
(рис.6). Углом наклона  прямой к оси
прямой к оси 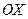 называется угол, на который нужно повернуть вокруг начала координат против движения часовой стрелки ось абсцисс так, чтобы она стала параллельна данной прямой. Тангенс угла наклона
называется угол, на который нужно повернуть вокруг начала координат против движения часовой стрелки ось абсцисс так, чтобы она стала параллельна данной прямой. Тангенс угла наклона  прямой называется угловым коэффициентом прямой и означается буквой
прямой называется угловым коэффициентом прямой и означается буквой 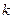 . Итак,
. Итак,
|
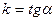 (5)
(5)
|

| |||||
| |
| ||||
Заметим, что если  острый угол, то
острый угол, то 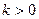 , если тупой, то
, если тупой, то 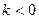 , если
, если  , то
, то 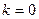 , если
, если  , то
, то 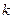 не существует.
не существует.
Пусть требуется найти уравнение прямой  , если
, если  проходит через точку
проходит через точку  и имеет угловой коэффициент
и имеет угловой коэффициент 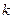 . Согласно формуле (2) уравнение любой прямой, проходящей через точку
. Согласно формуле (2) уравнение любой прямой, проходящей через точку  , запишется в виде
, запишется в виде
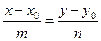 ,
,
где 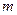 и
и  есть координаты направляющего вектора
есть координаты направляющего вектора  . В качестве направляющего вектора прямой
. В качестве направляющего вектора прямой  примем единичный вектор
примем единичный вектор 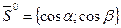 , составляющий с осью
, составляющий с осью 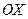 тот же угол
тот же угол  , что и прямая
, что и прямая  .
.
| 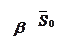 | |||

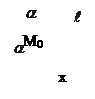 | |||
| |
Так как  , то
, то  . Полагая
. Полагая  , получим
, получим
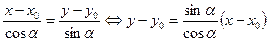 Û
Û
Û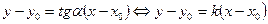 . (6)
. (6)
Уравнение (6) называется уравнением прямой по точке и угловому коэффициенту.
7. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми.
Пусть прямая  наклонена под углом
наклонена под углом  к оси
к оси  и пересекает ось
и пересекает ось  в точке
в точке  (рис.8). Уравнение
(рис.8). Уравнение  согласно формуле (6) при
согласно формуле (6) при  запишется в виде
запишется в виде
|
 . (7)
. (7)
|

| |||||||
| |||||||
| |
| ||||||
Уравнение (7) называется уравнением прямой с угловым коэффициентом.
Частные случаи:
1) если  , то уравнение примет вид
, то уравнение примет вид  . Это есть уравнение прямой, проходящей через начало координат;
. Это есть уравнение прямой, проходящей через начало координат;
2) если 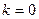 , то
, то 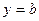 есть уравнение прямой, параллельной оси
есть уравнение прямой, параллельной оси 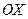 ;
;
3) если 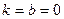 , то
, то 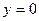 - уравнение самой оси
- уравнение самой оси 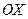 .
.
Пусть на плоскости  даны две пересекающиеся прямые
даны две пересекающиеся прямые 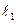 и
и 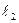 (рис.9).
(рис.9).
| 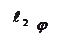 | ||||
| |||||
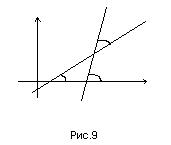

Пусть прямые 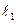 и
и 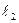 даны уравнениями
даны уравнениями 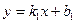 и
и  . Требуется определить угол
. Требуется определить угол  между ними. Предположим, что прямые не перпендикулярны и вычислим
между ними. Предположим, что прямые не перпендикулярны и вычислим 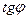 . Непосредственно из рис.9 найдем, что
. Непосредственно из рис.9 найдем, что 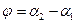 . Тогда
. Тогда
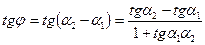 . Но
. Но  .
.
Следовательно, 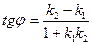 . (8)
. (8)
Итак, если угол  отсчитывается от прямой
отсчитывается от прямой 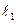 к прямой
к прямой 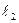 и
и 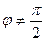 , то угол между прямыми может быть найден с помощью формулы (8).
, то угол между прямыми может быть найден с помощью формулы (8).
Заметим, что если 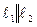 , то
, то 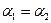 . Тогда
. Тогда 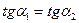 .
.
Следовательно, 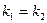 . (9)
. (9)
Обратно, если 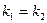 , то
, то 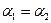 Û
Û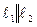 .
.
Таким образом, равенство (9) является необходимым и достаточным условием параллельности двух прямых.
Пусть 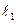 ^
^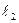 , тогда формула (8) теряет свой смысл. Но в этом случае
, тогда формула (8) теряет свой смысл. Но в этом случае 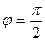 и
и 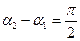 . Тогда
. Тогда  .
.
Следовательно,
 или
или  . (10)
. (10)
Нетрудно проверить, что из  следует, что
следует, что 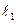 ^
^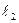 . Условие (10) является условием перпендикулярности двух прямых.
. Условие (10) является условием перпендикулярности двух прямых.
ПРИМЕР 6.1. Найти проекцию точки  на прямую
на прямую  .
.
На плоскости  проведем прямую
проведем прямую  и построим точку
и построим точку 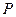 . Обозначим через
. Обозначим через 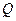 проекцию точки
проекцию точки 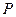 на прямую
на прямую  (рис.10).
(рис.10).

|
Уравнение прямой 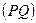 будем искать в форме уравнения прямой по точке и угловому коэффициенту, т.е. в форме
будем искать в форме уравнения прямой по точке и угловому коэффициенту, т.е. в форме  . Подставляя значения
. Подставляя значения 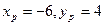 , получим
, получим 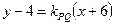 . Прямые
. Прямые 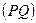 и
и  перпендикулярны. Тогда согласно формуле (10)
перпендикулярны. Тогда согласно формуле (10)  . Но
. Но  , тогда
, тогда  . Следовательно, уравнения
. Следовательно, уравнения 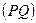 запишется в виде
запишется в виде 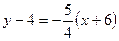 или
или 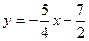 .
.
Точка 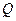 принадлежит обеим прямым
принадлежит обеим прямым  и
и 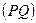 . Следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Тогда координаты точки
. Следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Тогда координаты точки 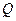 найдутся из системы
найдутся из системы
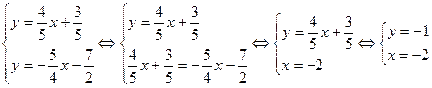
Ответ: 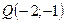 .
.
8. Общее уравнение прямой.
Как уже известно, уравнение 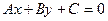 ,
, 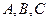 - действительные числа, является общим алгебраическим уравнением первой степени относительно двух переменных
- действительные числа, является общим алгебраическим уравнением первой степени относительно двух переменных 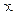 и
и 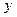 . Установленные ранее формы уравнения прямой являются также алгебраическими уравнениями первой степени относительно
. Установленные ранее формы уравнения прямой являются также алгебраическими уравнениями первой степени относительно  и
и 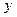 и при помощи простейших действий могут быть приведены к форме
и при помощи простейших действий могут быть приведены к форме
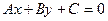 . (11)
. (11)
Покажем, что уравнение при любых 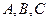 , кроме
, кроме 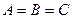 , определяет прямую на координатной плоскости
, определяет прямую на координатной плоскости  . Действительно, полагая одно из чисел
. Действительно, полагая одно из чисел  или
или  , например,
, например,  , неравным нулю, получим
, неравным нулю, получим
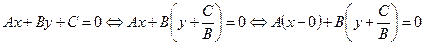 .
.
Сравнивая это уравнение с уравнением 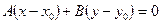 , найдем, что оно есть уравнение прямой, проходящей через точку
, найдем, что оно есть уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 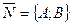 . Следовательно, и уравнение
. Следовательно, и уравнение 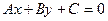 есть уравнение прямой.
есть уравнение прямой.
Уравнение (11)называется общим уравнением прямой.
Частные случаи:
1) если 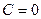 , то
, то 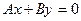 . Это есть уравнение прямой, проходящей через начало координат;
. Это есть уравнение прямой, проходящей через начало координат;
2) если 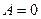 ,
,  , то
, то  есть уравнение прямой, параллельной оси
есть уравнение прямой, параллельной оси 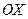 ;
;
3) если 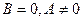 , то
, то 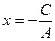 . Это уравнение прямой, параллельной оси
. Это уравнение прямой, параллельной оси 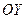 . В частности, при
. В частности, при 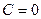 получим
получим 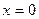 -уравнение оси
-уравнение оси 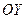 .
.
ПРИМЕР 7.1. Дана прямая 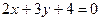 . Составить уравнение прямой, проходящей через точку
. Составить уравнение прямой, проходящей через точку 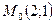 параллельно данной прямой.
параллельно данной прямой.
Решение. Так как 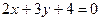 , то
, то 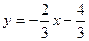 . Сравнивая полученное уравнение с уравнением
. Сравнивая полученное уравнение с уравнением  , получим, что
, получим, что 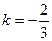 .
.
Искомая прямая должна быть параллельна данной прямой. Следовательно, согласно формуле (9) ее угловой коэффициент 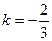 . Итак, для искомой прямой известна ее точка
. Итак, для искомой прямой известна ее точка 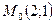 и угловой коэффициент
и угловой коэффициент 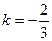 . Тогда ее уравнение найдем по формуле (6)
. Тогда ее уравнение найдем по формуле (6)
 .
.
Заметим попутно, что коэффициенты  у искомой и данной прямых оказались равными. Этт факт не случаен (доказать самостоятельно).
у искомой и данной прямых оказались равными. Этт факт не случаен (доказать самостоятельно).
Ответ: 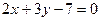 .
.
ВЫВОД. Заканчивая изложение вопроса о прямой линии на плоскости, еще раз отметим, что всякое алгебраическое уравнение первой степени относительно двух переменных 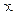 и
и 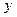 , т.е. уравнение вида
, т.е. уравнение вида 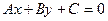 , есть уравнение прямой линии на плоскости
, есть уравнение прямой линии на плоскости  . И наоборот, уравнение любой прямой на этой плоскости является алгебраическим уравнением вида
. И наоборот, уравнение любой прямой на этой плоскости является алгебраическим уравнением вида 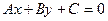 .
.
9. Кривые второго порядка.
– Конец работы –
Эта тема принадлежит разделу:
МАТРИЦЫ И ИХ ВИДЫ
ОПЕРАЦИИ НАД МАТРИЦАМИ... Равенство матриц... Две матрицы А и В называются равными А В если они имеют одинаковые размеры и их соответствующие элементы равны...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Уравнение прямой по двум точкам.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов