Метод Гаусса. Задачи

1. Доказать утверждения 1 и 2.

2. Пусть система (1.1) имеет решения 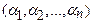и 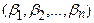. Найти систему линейных уравнений с теми же коэффициентами при переменных, как и в системе (1.1), имеющую решение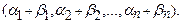

3. Пусть система (1.1) имеет решение 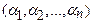. Найти систему линейных уравнений с теми же коэффициентами при переменных, как и в системе (1.1), имеющую решение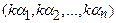

4. Решить системы линейных уравнений методом Гаусса:

а) ,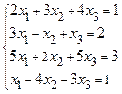

б) ,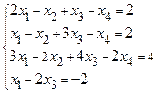

в)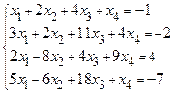

5. Для откорма скота на ферме в ежедневный рацион каждого животного должно включаться 5 видов питательных веществ в количествах 76, 360, 155, 294, 231 единиц соответственно. При этом используется 6 видов кормов, стоимости одной весовой единицы которых равны соответственно 15, 3, 8, 1, 20.5, 13.5 ден. ед. Дана матрица А норм содержания питательных веществ в кормах, в которой на позиции 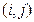находится число единиц -го вида питательных веществ, содержащихся в единице веса 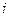-го вида кормов. Определить состав ежедневного рациона для откорма скота на ферме при дополнительном условии, что общая стоимость всего рациона должна равняться 250 ден. ед.

а) ;

б) .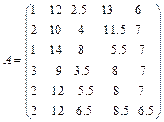

6. Для сохранения здоровья человек должен потреблять в сутки определенное количество питательных веществ трех видов, содержащихся в 5 видах пищи. Цена единицы веса пищи каждого вида равна соответственно 10, 5, 6, 8, 10 ден. ед. Суточные нормы питательных веществ равны соответственно 10, 12, 20 единиц. Дана также матрица А норм содержания питательных веществ в единице веса пищи, в которой на позиции 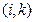находится норма содержания питательного вещества 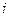-го вида в единице веса пищи -го вида. Определить количество пищи каждого вида, включаемой в суточную диету при условиях, что вариант диеты должен иметь стоимость в 85 ден. ед., а количество пищи второго типа должно равняться количеству пищи четвертого вида.

а) ;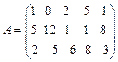

б) .

7. Предприятие выпускает пять видов продукции, используя при этом сырье трех видов. Дана матрица расхода сырья:

,

в которой на позиции 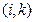находится величина, равная количеству сырья 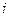-го вида, расходуемому на производство единицы продукции -го вида. Запасы сырья по типам составляют 1325, 340, 208 вес. ед. соответственно. Прибыль в ден. ед. за единицу готовой продукции каждого вида равна 16, 10, 14, 12, 12 соответственно. Необходимо спрогнозировать объемы выпуска продукции при следующих условиях: прибыль должна составить 15620 ден. ед., а объемы выпуска продукции второго и первого видов должны быть одинаковы. Определить также зависимость объемов выпускаемой продукции от планируемой величины прибыли, которая должна будет находиться в диапазоне от 15000 до 20000 ден. ед.

8. Доказать следствия 3 и 4.

9. Доказать следствие 1.7.

10. Доказать. теорему 1.13: квадратная матрица А вырождена, если и только если такой является матрица .

11. Доказать теорему 1.14: добавление нового столбца к матрице не нарушает линейную независимость ее строк; аналогично добавление новой строки не нарушает линейную независимость ее столбцов.

12. Доказать теорему 1.15: неоднородная система линейных уравнений с квадратной матрицей А имеет единственное решение, если и только если строки (столбцы) матрицы А линейно независимы.

13. Доказать теорему 1. 16: любую линейно независимую систему векторов, не являющуюся базисом в пространстве , можно дополнить новыми векторами до базиса этого пространства.

14. Доказать следующее утверждение. Теорема 1.17. Пусть дана система 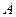из 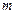линейно независимых векторов пространства и 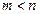. Доказать, что если ненулевой вектор ортогонален с каждым вектором из А, то система векторов А, будет также линейно независимой.

15. Доказать, что векторы , , образуют базис в пространстве 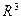, а также представить вектор 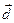в виде линейной комбинации векторов , , .

а) , , , ;

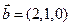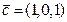б) , , , .

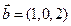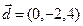16. Дополнить линейно независимую систему векторов до базиса:

а) ;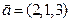

б) , ;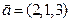

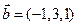в) , ;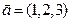

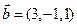г) , ;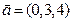

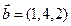д) , ;