Ответы, указания, решения.

2. Ответ: искомая система будет иметь следующий вид:

.

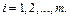3.Ответ: искомая система будет иметь следующий вид:

.

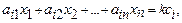
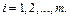4.в). Решение. Составим расширенную матрицу данной системы уравнений и элементарными преобразованиями приведем ее к эквивалентному виду, содержащему базис переменных:

 

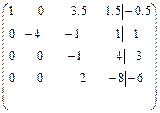
Вторая матрица получена из первой путем поочередного умножения первой строки на (-3), (-2), (-5) и прибавления соответственно ко второй, третьей и четвертой строкам первой матрицы. Третья же матрица получена из предыдущей путем поочередного умножения второй строки на 0ю5, -3, -4 и прибавления соответственно к первой, третьей и четвертой строкам. Четвертая матрица получена из предыдущей путем поочередного умножения третьей строки на 3ю5,-1, 2 и прибавления соответственно к первой, второй и четвертой строкам. Последней матрице соответствует система уравнений:

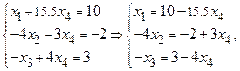
в которой имеется базис переменных . Переменная 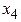является свободной. Поэтому исходная система имеет следующие решения:

,

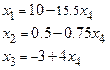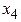- любое действительное число.

5 б). Ответ: 2.85, 4.17, 3.04, 14.35, 4.23, 5.14.

6 б). Ответ: 2.697, 0.611, 6.27, 0.611, 1.247.

7.Указание. Ввести исходные данные: матрицу рас хода сырья, вектор-строки и 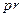запасов сырья и доходов от реализации единицы продукции соответственно. Задать начальные значения переменных и определить функцию зависимости объемов выпуска продукции от параметра 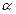, задающего величину прибыли от реализации готовой продукции:

, , ,

, , , .

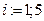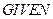
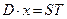Определить объемы выпуска продукции каждого вида при величине прибыли в 15620 ден. ед., а также при изменении величины прибыли в диапазоне от 15000 до 20000 с шагом изменения, равным 1000:

, .

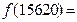
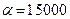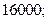
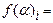Замечание. Здесь и в дальнейшем запись типа 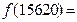, когда справа от знака равенства отсутствует результат, отнюдь не является опечаткой. Просто после редактирования формульных областей на экране компьютера такие результаты появляются, только если включен режим Автоматические вычисления(Automatic Calculation) или пользователь самостоятельно инициировал обновление вычислений.

10. Указание: воспользоваться следствием 7.

11. Доказательство.Предположим, что в матрице с линейно независимыми столбцами добавлена одна строка. Полученную матрицу обозначим . Очевидно, что система уравнений содержит все уравнения системы 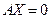. Поэтому множество решений системы является подмножеством решений системы 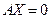. Но система 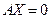имеет только нулевое решение в силу следствия 3. Следовательно, и вторая система имеет только нулевое решение, что опять-таки по следствию 3 означает линейную независимость столбцов матрицы .

Остальная часть утверждения (касающаяся добавления нового столбца) следует из только что доказанного – достаточно только перейти к рассмотрению транспонированной матрицы.

12. Доказательство.Согласно следствию 6 строки (столбцы) матрицы А линейно независимы, если и только если система элементарными преобразованиями может быть приведена к системе вида с тем же множеством решений и в которой единичная матрица Е того же порядка, что и А. Это завершает доказательство, если учесть, что система вида имеет единственное решение .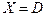

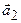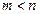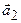13. Доказательство.Пусть дана линейно независимая система векторов , , … , и . Тогда из следствия 2 вытекает существование ненулевого вектора , ортогонального с каждым вектором этой системы. Если новая система векторов , , … , , линейно зависима, то по теореме 1.7 вектор представим в виде линейной комбинации векторов первоначальной системы. Но это невозможно, как было показано в конце доказательства следствия 5. 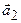Итак, система векторов , , … , , линейно независима. Повторяя рассуждения, через шагов придем к линейно независимой системе из 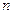векторов, которая и будет искомым базисом в силу следствия 5.

14. Указание:воспользоваться решением задачи 13.

15 б). Решение.В силу следствия 5 в пространстве 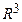любая тройка линейно независимых векторов образует базис. Поэтому необходимо доказать линейную независимость векторов , , . Кроме того, представить вектор 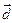в виде линейной комбинации векторов , , - это значит решить линейную систему уравнений . Решим эту систему методом Гаусса. Одновременно отметим, что в силу теоремы 1.15 векторы , , линейно независимы, если и только если эта система имеет единственное решение. Итак:

..

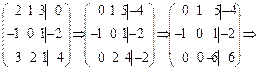Откуда имеем: , , т.е. .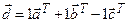

16 д). Решение.Вначале найдем ненулевой вектор , ортогональный векторам и . Для этого необходимо решить однородную систему линейных уравнений:

.

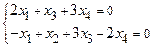Решим ее методом Гаусса:

.

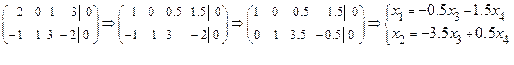Пусть . Тогда ,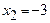. Вектор 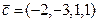- искомый. В силу утверждения задачи 14 система векторов , , линейно независима. Найдем теперь ненулевой вектор 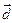, ортогональный с векторами , , . Для этого необходимо решить однородную систему линейных уравнений:

, .

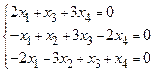Решим ее методом Гаусса:

.

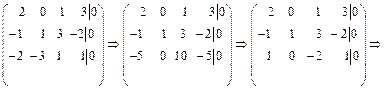
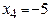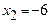Пусть . Тогда , , . Вектор 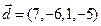искомый. Опять-таки в силу утверждения задачи 14 система векторов , , , 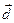линейно независима. Но тогда эта система в силу следствия 5 является базисом пространства .