Понятие производной

Рассмотрим график непрерывной функции у=f(x). Возьмем на этом графике точку М₀(x₀, у₀). Определим тангенс угла наклона касательной прямой к графику у=f(х), проведенной в точке М₀ (рис.1).

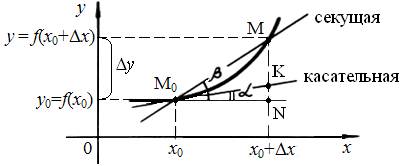
Рис. 1

Точка М₀ имеет координаты х₀, у₀=f(х₀). Дадим переменной х приращение Dx и переместимся по графику из точки М₀ в точку М с координатами: абсциссой х₀ + Dх, ординатой у₀ + Dy = f(х₀ + Dх). При перемещении из точки М₀ в точку M значение функции изменилось на величину Dу. Это изменение называется приращением функции и вычисляется так:

Dy = y – y₀ = f(x₀+Dx) – f(x₀).

Проведем секущую прямую М₀М. Тангенс угла наклона к оси ОХ (угловой коэффициент) секущей может быть найден из прямоугольного треугольника М₀МN как отношение противолежащего катета |MN| к прилежащему |M₀N|:

.

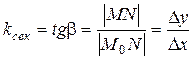Когда точка М вдоль кривой будет перемещаться к точке M₀, секущая М₀М будет вращаться вокруг точки M₀ и неограниченно приближаться к некоторой прямой М₀К с углом наклона a (М₀М ® М₀К). Это предельное положение секущей является касательной к графику у=f(х) в точке М₀.

В этом случае неограниченно уменьшаются приращение аргумента Dх (Dх®0) и приращение функции Dу®0 (наша функция непрерывна).

Угол b наклона секущей к положительному направлению оси OX превратится в угол наклона касательной a. Тогда угловой коэффициент касательной прямой k получим так:

,

т.е. угловой коэффициент касательной есть предел отношения приращения функции Dу к приращению аргумента Dх при стремлении Dх к нулю.

Определение 1. Производной функции у=f(х) в точке х₀ называется предел отношения приращения функции Dу = f(х₀+Dх) – f(x₀) к приращению аргумента Dх при стремлении Dх к нулю, если такой предел существует.

.

Другие обозначения производной функции в точке х₀:

у'(х₀), .

Нахождение производной функции называется дифференцированием функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке.

Определение 2. Функция f(х) имеет производную на интервале (a, b), если производная f'(х₀) существует в каждой точке х₀ этого интервала.

Учитывая это, в дальнейшем иногда будем опускать индекс «0» у величины х₀ и записывать производную так: f'(х).

Производную функции f(х) можно вычислять при различных значениях х (не только в точке х₀), т.е. величина производной зависит от значения аргумента х. Поэтому, если функция f(х) имеет производную в каждой точке множества X, то производная f'(x) также является функцией от аргумента х, определенной на множестве Х.