Основные свойства определителей

Лекция 1.

Определение матрицы. Определители второго и третьего порядков, их основные свойства. Миноры и алгебраические дополнения, разложение определителя по строке (столбцу). Методы вычисления определителей. Понятие об определителе n-го порядка.

 

Определение 1.1. Матрицей называется прямоугольная таблица чисел.

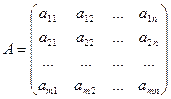
Обозначения: А – матрица, 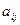- элемент матрицы, 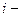номер строки, в которой стоит данный элемент, номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

 

Определение 1.2. Числа m и n называются размерностями матрицы.

 

Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

 

Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.

 

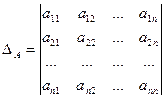
Определение 1.4.Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

.

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

 

Примеры.

 

1. 2.

 

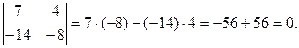
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

 

Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

 

образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:

 

 

Примеры.

1.

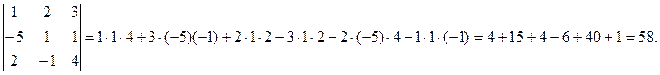
2.

 

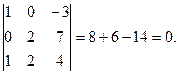
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированнойпо отношению к матрице А, элементы которой связаны с элементами А соотношением a`_ij = a_ji .

 

 

Основные свойства определителей.

  Свойство 1. Определитель не изменяется при транспонировании, т.е.

Разложение определителя по строке.

Определение1. 7. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит…   Обозначение: выбранный элемент определителя, его минор.

Лекция 2. Системы линейных уравнений. Метод Гаусса. Правило Крамера.

  Определение 2.2. Линейной комбинацией переменных называется результат…  

Метод Гаусса решения линейных систем.

  Примеры: 1. . Единственным решением является пара чисел х = 1, у = 2.

Правило Крамера.

Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель , элементами которого являются коэффициенты при неизвестных: .  

Если система (2.3) имеет единственное решение, определяемое по формулам: .

Если ==0, система имеет бесконечно много решений.

Если =0, а хотя бы один из система не имеет решений.

 

Примеры:

1. Рассмотрим систему 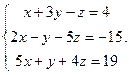, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:

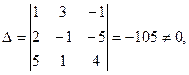следовательно, система имеет единственное решение.

Отсюда

 

2. . Здесь 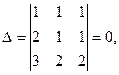поскольку имеет два одинаковых столбца.

Следовательно, система не имеет единственного решения. Найдем и

поэтому система имеет бесконечно много решений.

 

3. . Для этой системы но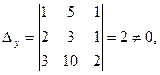

следовательно, решений нет.

 

 

Лекция 3.

Операции над матрицами, их свойства. Обратная матрица, ее вычисление.

Матричная запись системы линейных уравнений. Решение линейных систем с помощью обратной матрицы.

Определение 3.1. Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.

 

Определение 3.2. Матрица называется нулевой, если все ее элементы равны 0.

 

Определение 3.3. Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0.

 

Линейные операции над матрицами.

1. Сложение матриц.

 

Определение 3.4. Суммой матриц А и В одинаковой размерности m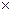n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения:

1. А + В = В + А.
2. (А + В) + С = А + (В + С) .
3. Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

 

Пример.

 

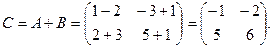
2. Умножение матрицы на число.

 

Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Свойства умножения матрицы на число:

1. (km)A=k(mA).
2. k(A + B) = kA + kB.
3. (k + m)A = kA + mA.

 

Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.

 

Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.

 

Пример.

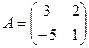. Тогда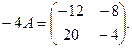

 

Перемножение матриц.

  Определение 3.6. Произведением матрицы А размерности mp и матрицы В…  

Обратная матрица.

Определение 3.7. Квадратная матрица А называется вырожденной, если , и невырожденной, если .   Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е.…

Решение линейных систем с помощью обратной матрицы.

- матрица системы, - столбец неизвестных, - столбец свободных членов. Тогда систему (2.3) можно записать в виде… Пусть матрица А – невырожденная, тогда существует обратная к ней матрица

Лекция 4.

Ранг матрицы. Теорема о ранге. Вычисление ранга матрицы. Совместность систем линейных уравнений. Теорема Кронекера-Капелли. Структура общего решения однородной системы линейных уравнений. Общее решение неоднородной системы линейных уравнений.

Определение 4.1. Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.

 

Замечание. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.

 

Определение 4.2. Ранг матрицы – это порядок ее наибольшего ненулевого минора.

 

Обозначения: r(A), R(A), Rang A.

 

Замечание. Очевидно, что значение ранга матрицы не может превышать меньшей из ее размерностей.

 

Примеры:

1. 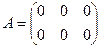, r(A)=0.

2. 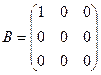. Матрица В содержит единственный ненулевой элемент - 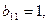являющийся минором 1-го порядка. Все определители более высоких порядков, составленные из элементов этой матрицы, будут содержать 0-ю строку и поэтому равны 0. Следовательно, r(B)=1.

3. 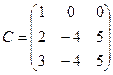. Единственным минором 3-го порядка является определитель матрицы С, но он равен 0, поскольку содержит пропорциональные столбцы. Следовательно, r(C)<3.

Для того, чтобы доказать, что r(C)=2, достаточно указать хотя бы один минор 2-го порядка, не равный 0, например, 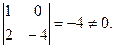Значит, r(C)=2.

4. следовательно, r(E)=3.

 

Замечание. Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:

1) транспонирование

2) умножение строки на ненулевое число

3) перестановка строк

4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число

5) вычеркивание нулевой строки.

Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.

Пример. Найдем ранг матрицы 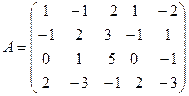. Теоретически ранг этой матрицы может принимать значения от 1 до 4, так как из элементов матрицы можно создать миноры по 4-й порядок включительно. Но вместо того, чтобы вычислять все возможные миноры 4-го, 3-го и т.д. порядка, применим к матрице А эквивалентные преобразования. Вначале добьемся того, чтобы в первом столбце все элементы, кроме первого, равнялись 0. Для этого запишем вместо второй строки ее сумму с первой, а вместо третьей – разность третьей и удвоенной первой:

 

.

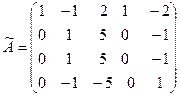
Затем из третьей строки вычтем вторую, а к четвертой прибавим вторую:

.

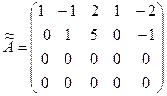После вычеркивания нулевых строк получим матрицу размерности для которой максимальный порядок миноров, а, следовательно, и максимально возможное значение ранга равно 2:

.

Ее минор 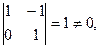следовательно,

 

Теорема о ранге.

Определение 4.3. Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.   Определение 4.4. Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не…

Совместность линейных систем.

Определение 4.5. Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.   Определение 4.6. Совместная линейная система называется определенной, если она имеет единственное решение, и…

Общее решение однородной линейной системы.

. (4.2) Отметим, что такая система всегда совместна, поскольку имеет нулевое решение… Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда…

Структура общего решения неоднородной линейной системы.

Рассмотрим неоднородную линейную систему (2.2): . Докажем следующие свойства ее решений:

Лекция 5.

  Определение 5.1. Вектором называется направленный отрезок.  

Линейные операции над векторами.

Определение 5.4. Суммой a + b векторовa и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

b

A+b

a

Замечание. Такое правило сложения векторов называют правилом треугольника.

 

Свойства сложения:

Свойство 1. a + b = b + a.

Доказательство. Приложим векторы а и b к общему началу и рассмотрим параллелограмм

AOBC. Из определения 5.4 и треугольника ОВС следует, что ОС=b+a,а из треугольника

ОАС – ОС=а+b.Свойство 1 доказано.

В а С Замечание. При этом сформулировано еще одно правило

b bсложения векторов – правило параллелограмма: сумма

a+b=векторов a и b есть диагональ параллелограмма, построенно-

=b+aго на них как на сторонах, выходящая из их общего начала.

О А

А

Свойство 2. (a+b)+c=a+(b+c).

b Доказательство. Из рисунка видно, что

A a+b B (a+b)+c=(OA+AB)+BC=OB+BC=OC,

A a+(b+c)=OA+(AB+BC)=OA+AC=OC.

b+с O cС Свойство 3. Для любого вектора a существует нулевой векторО такой, что a+О=а.

B

 

Определение 5.6. Произведениемkaвектора а на число k называется вектор b, коллинеарный векторуа, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

Свойства умножения вектора на число:

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.

 

Базис и координаты вектора.

Определение 5.7. Линейной комбинацией векторов а1, а2,…,аnназывается выражение вида: k1a1 + k2a2 +…+ knan, (5.1) где ki – числа.  

Скалярное произведение векторов.

Определение 5.14. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними: ab = |a||b| cosφ . (5.4) Обозначения скалярного произведения: ab, (ab), a·b .

A b

abc – правая тройка abc – левая тройка

 

Замечание. В дальнейшем будем рассматривать только правые системы координат, т.е. системы, базисные векторы которых образуют правую тройку.

 

Векторное произведение векторов.

Определение 6.2. Вектор с называется векторным произведениемвекторов аи b, если: 1) |c| = |a||b|sinφ, где φ – угол между а и b. 2) ca, cb.

Смешанное произведение векторов.

Обозначение: abc= [ab]c. Свойства смешанного произведения. 1) Смешанное произведение [ab]c равно объему параллелепипеда, построенного на приведенных к общему началу векторах…

Лекция 7.

Линии на плоскости и их уравнения. Прямая на плоскости. Различные формы уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.

 

Пусть на плоскости задана декартова система координат и некоторая линия L.

 

Определение 7.1. Уравнение

Ф(х,у) = 0 (7.1)

называется уравнением линии L, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты ни одной точки, не лежащей на линии L.

 

Пример.

(х – а)² + (y – b)² = R² - уравнение окружности радиуса R с центром в точке (a,b).

 

Замечание. Часто удобно использовать параметрическиеуравнения линии:

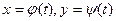, (7.2)

где функци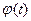и и 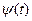непрерывны по параметру t.

 

Прямая на плоскости.

Рассмотрим различные виды уравнений прямой на плоскости. Пусть прямая проходит через точку М0 (x0,y0) перпендикулярно вектору n =… А(х – х0) + В(у – у0) = 0 - (7.3)

Неполные уравнения прямой.

1) С = 0 - прямая Ах + Ву = 0 проходит через начало координат. 2) В = 0 - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой… 3) А = 0 - прямая Ву + С = 0 параллельна оси Ох.

Угол между прямыми. Условия параллельности и

  1. Если прямые L1 и L2 заданы общими уравнениями А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0,

Лекция 8.

Прямая и плоскость в пространстве. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью.

Отметим, что многие утверждения и формулы, касающиеся плоскости в пространстве, доказываются и выводятся так же, как при изучении прямой на плоскости, поэтому в этих случаях будут даваться ссылки на предыдущую лекцию.

 

Плоскость в пространстве.

Получим сначала уравнение плоскости, проходящей через точку М0(х0 ,у0 ,z0) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для… A(x - x0) + B(y - y0) + C(z - z0) = 0. (8.1) Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через…

Неполные уравнения плоскости.

Рассмотрим возможные виды неполных уравнений: 1) D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат. 2) А = 0 – n = {0,B,C}Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.

Угол между плоскостями. Условия параллельности и

Перпендикулярности плоскостей.

A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, то очевидно, что угол между ними равен углу между их нормалями, то есть между… (8.4)

Прямая в пространстве.

Замечание. Прямую в пространстве невозможно задать одним уравнением. Для этого требуется система двух или более уравнений. Первая возможность составить уравнения прямой в пространстве – представить эту… A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, где коэффициенты A1,B1,C1 и A2,B2,C2 не пропорциональны:

Угол между прямыми. Угол между прямой и плоскостью.

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида и косинус угла между ними можно найти по формуле: . (8.14)

Лекция 9.

Кривые второго порядка. Эллипс, гипербола и парабола, их свойства и канонические уравнения.

  Если такая плоскость пересекает все образующие одной полости конуса, то в…  

Эллипс.

  Замечание. При совпадении точек F1 и F2 эллипс превращается в окружность. Выведем уравнение эллипса, выбрав декартову систему

Гипербола.

  Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения… |r1 - r2| = 2a, откуда Если обозначить b² = c² - a², отсюда можно получить

Парабола.

Определение 9.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно… у Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина

Лекция 10.

Поверхности второго порядка. Канонические уравнения основных поверхностей второго порядка: эллипсоидов, гиперболоидов и параболоидов.

 

Поверхности второго порядка.

Определение 10.1. Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:

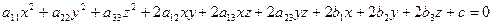- (10.1)

уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.

Эллипсоид.

. (10.2) Уравнение (10.2) называется каноническим уравнением эллипсоида. Величины a, b,… Координаты точек эллипсоида удовлетворяют неравенствам - a £ x £ a, - b £ y £ b, - c £ z…

Гиперболоиды.

Определение 10.3. Гиперболоидами называются поверхности, которые в некоторой системе прямоугольных декартовых координат определяются каноническими… , (10.3) . (10.4)

Параболоиды.

, (10.5) , (10.6) где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (10.5),…