рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вид работы: Лекции
- /
- Системы линейных уравнений. Основные определения
Реферат Курсовая Конспект
Системы линейных уравнений. Основные определения
Системы линейных уравнений. Основные определения - Лекция, раздел Математика, Лекции 3. Системы Линейных Уравнений И Методы Их Решени...
Лекции 3. Системы линейных уравнений и методы их решения
План лекции.
1. Системы линейных уравнений. Основные определения.
2. Метод Гаусса решения систем линейных уравнений.
3. Критерий совместности систем линейных уравнений.
4. Матричный метод решения систем линейных уравнений.
5. Метод Крамера решения систем линейных уравнений.
6. Однородная система линейных уравнений, условие существования ненулевых решений.
1.
Системой 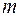 линейных уравнений с
линейных уравнений с  неизвестными называются соотношения вида
неизвестными называются соотношения вида
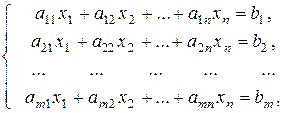 (1)
(1)
где  - коэффициенты системы,
- коэффициенты системы, 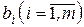 - свободные члены,
- свободные члены,  - неизвестные системы.
- неизвестные системы.
Система (1) называется однородной, если все свободные члены  . Система (1) называется неоднородной, если хотя бы один из свободных членов
. Система (1) называется неоднородной, если хотя бы один из свободных членов  .
.
Решением системы называется совокупность чисел  , при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называться несовместной или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.
, при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называться несовместной или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.
Совместная система называется определенной, если она имеет единственное решение. Если совместная система имеет более одного решения, то она называется неопределенной. Однородная система всегда совместна, так как имеет, по крайней мере, нулевое решение 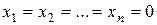 . Выражение для неизвестных
. Выражение для неизвестных  из которого можно получить любое конкретное решение системы, называют ее общим решением, а любое конкретное решение системы – ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны), если каждое решение одной из них является решением другой или обе системы несовместны.
из которого можно получить любое конкретное решение системы, называют ее общим решением, а любое конкретное решение системы – ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны), если каждое решение одной из них является решением другой или обе системы несовместны.
Рассмотрим методы решения систем линейных уравнений.
2.
Одним из основных методов решения систем линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных. Суть этого метода состоит в сведении системы линейных уравнений к ступенчатому виду. При этом над уравнениями приходится проводить следующие элементарные преобразования:
1. Перестановка уравнений системы.
2. Прибавление к одному уравнению другого уравнения.
3. Умножение обеих частей уравнения на число, отличное от нуля.
4. Прибавление к одному уравнению другого, умноженного на некоторое число, отличное от нуля.
5. Вычеркивание уравнений вида 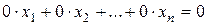 , т.е. тождеств
, т.е. тождеств 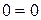 .
.
В результате элементарных преобразований система преобразуется в эквивалентную ей систему.
Рассмотрим алгоритм метода Гаусса. Пусть дана система вида (1). Предположим, что в этой системе коэффициент  . Заметим, что этого всегда можно достигнуть перестановкой уравнений системы. Для исключения неизвестной
. Заметим, что этого всегда можно достигнуть перестановкой уравнений системы. Для исключения неизвестной  во всех уравнениях, начиная со второго, умножим первое уравнение системы последовательно на числа
во всех уравнениях, начиная со второго, умножим первое уравнение системы последовательно на числа 
 и добавим соответственно ко 2-му, 3-му, ...,
и добавим соответственно ко 2-му, 3-му, ..., 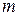 - му уравнению системы. В результате система примет вид:
- му уравнению системы. В результате система примет вид:
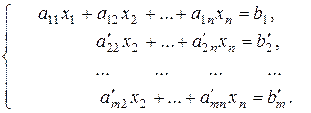
Продолжая этот процесс дальше, исключаем неизвестную  из всех уравнений, начиная с третьего. Для этого умножим второе уравнение на числа
из всех уравнений, начиная с третьего. Для этого умножим второе уравнение на числа  и добавим к 3-му, ..., к
и добавим к 3-му, ..., к 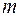 - му уравнению системы. Следующие шаги метода Гаусса осуществляются аналогично. Если в результате преобразований получится тождественное уравнение, то вычеркнем его из системы. Если на некотором шаге метода Гаусса получается уравнение вида:
- му уравнению системы. Следующие шаги метода Гаусса осуществляются аналогично. Если в результате преобразований получится тождественное уравнение, то вычеркнем его из системы. Если на некотором шаге метода Гаусса получается уравнение вида:
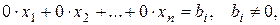 (2)
(2)
тогда рассматриваемая система несовместна, и дальнейшее ее решение прекращается. Если же уравнение вида (2) не встретится при выполнении элементарных преобразований, то не более чем через 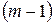 - шагов система (13.1) будет преобразована к ступенчатому виду:
- шагов система (13.1) будет преобразована к ступенчатому виду:
 (3)
(3)
где  . Если
. Если  , то говорят, что система свелась к треугольному виду. В этом случае система имеет единственное решение, которое находим, решая систему снизу вверх.
, то говорят, что система свелась к треугольному виду. В этом случае система имеет единственное решение, которое находим, решая систему снизу вверх.
Если 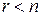 , то говорят, что система свелась к трапециидальному виду. В этом случае система является неопределенной. Для нахождения общего решения системы в этом случае выбирают
, то говорят, что система свелась к трапециидальному виду. В этом случае система является неопределенной. Для нахождения общего решения системы в этом случае выбирают  главных и
главных и  свободных неизвестных. Например, неизвестные
свободных неизвестных. Например, неизвестные 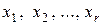 принимают за главные, а неизвестные
принимают за главные, а неизвестные  принимают за свободные. Переносим свободные неизвестные в правую часть уравнений и выражаем главные неизвестные через свободные. В результате получаем общее решение системы:
принимают за свободные. Переносим свободные неизвестные в правую часть уравнений и выражаем главные неизвестные через свободные. В результате получаем общее решение системы:
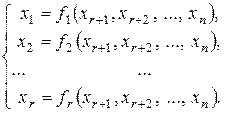 (4)
(4)
Для получения частного решения системы необходимо будет в (4) придать свободным переменным конкретные значения.
Заметим, что так как в методе Гаусса все преобразования выполняются над коэффициентами при неизвестных уравнений и свободными членами, то на практике обычно этот метод применяют к матрице, составленной из коэффициентов при неизвестных и столбца свободных членов. Эту матрицу называют расширенной. С помощью элементарных преобразований эту матрицу сводят к ступенчатому виду. После чего по полученной матрице восстанавливают систему и применяют к ней все предыдущие рассуждения.
Пример 1. Решить систему:
 .
.
Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:

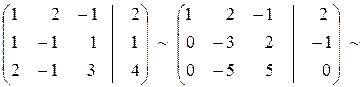


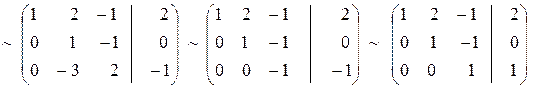
Матрица свелась к треугольному виду, следовательно система имеет единственное решение.
Восстанавливаем систему и решаем её снизу вверх.

Пример 2. Решить систему:

Решение. Составляем расширенную матрицу и сводим её к ступенчатому виду:


Данная система не совместна, так как последняя строка матрицы соответствует уравнению  , которое решения не имеет.
, которое решения не имеет.
Пример 3. Решить систему:

Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:


Матрица свелась к трапециидальному виду, следовательно система является неопределенной:
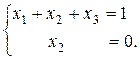
Пусть 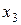 - свободная неизвестная. Тогда получаем общее решение системы:
- свободная неизвестная. Тогда получаем общее решение системы:

Замечание 1 . При решении однородной системы линейных уравнений методом Гаусса на практике выписывают основную, а не расширенную матрицу системы. И сводят ее к ступенчатому виду.
Замечание 2. Метод Гаусса применим для любой системы линейных уравнений, в том числе и для системы, у которой число уравнений не равно числу неизвестных.
Выяснить вопрос о совместности системы и о числе ее решений помогает следующая теорема.
Теорема (Критерий совместности системы линейных уравнений). Система линейных уравнений (1) совместна тогда и только тогда, когда ранг основной матрицы системы (матрицы 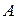 ) равен рангу расширенной матрицы (матрицы
) равен рангу расширенной матрицы (матрицы  ). В противном случае, т.е. если
). В противном случае, т.е. если 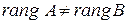 , то система не совместна. Если
, то система не совместна. Если  , где
, где 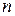 - число неизвестных системы, то система определенная. Если
- число неизвестных системы, то система определенная. Если  , то система неопределенная.
, то система неопределенная.
Применим эту теорему для рассмотренных в п.2 примеров.
Для примера 1.  и число неизвестных
и число неизвестных 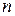 =3, т.е. система определенная.
=3, т.е. система определенная.
Для примера 2. 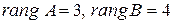 , поэтому система несовместна.
, поэтому система несовместна.
Для примера 3. 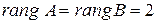 , число неизвестных
, число неизвестных 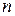 =3, поэтому система является неопределенной.
=3, поэтому система является неопределенной.
4.
Пусть дана система 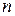 линейных уравнений с
линейных уравнений с 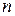 неизвестными:
неизвестными:
 (5)
(5)
Обозначим 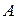 - матрицу из коэффициентов при неизвестных,
- матрицу из коэффициентов при неизвестных,  - матрицу-столбец из неизвестных,
- матрицу-столбец из неизвестных,  - матрицу-столбец свободных членов, т.е.
- матрицу-столбец свободных членов, т.е.
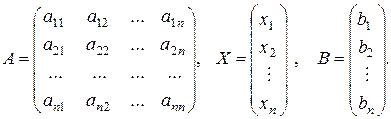
Несложно заметить, что тогда система (5) может быть записана в виде матричного уравнения
 (6)
(6)
Умножим слева обе части уравнения (6) на матрицу, обратную матрице 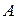 , т.е. на
, т.е. на  :
:
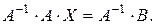 (7)
(7)
Учитывая что  из (7) получаем формулу для решения системы в матричной форме :
из (7) получаем формулу для решения системы в матричной форме :
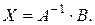 (8)
(8)
Пример 1. Решить систему в матричной форме:
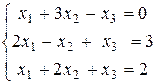 .
.
Решение: Запишем систему в матричной форме:

Обозначим
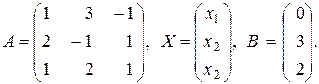
Найдем  :
:


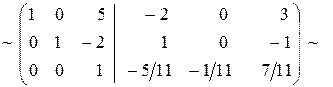
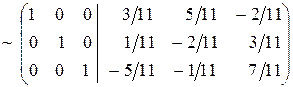 .
.
Отсюда
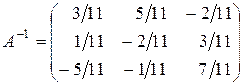
Получаем решение системы:

Таким образом,  .
.
Замечание. Матричный метод решения систем линейных уравнений применим только тогда, когда число уравнений системы равно числу неизвестных и матрица 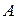 является невырожденной.
является невырожденной.
5.
Рассмотрим еще один метод решения систем линейных уравнений – метод Крамера, основанной на следующей теореме:
Теорема (правило Крамера). Если в системе 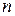 линейных уравнений с
линейных уравнений с 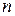 неизвестными (система вида (5) определитель, составленный из коэффициентов при неизвестных
неизвестными (система вида (5) определитель, составленный из коэффициентов при неизвестных  отличен от нуля, то система имеет единственное решение, которое находится по формулам
отличен от нуля, то система имеет единственное решение, которое находится по формулам
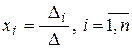 , (9)
, (9)
где 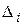 - определитель, полученный из определителя
- определитель, полученный из определителя  замененный
замененный  -го столбца столбцом свободных членов.
-го столбца столбцом свободных членов.
Доказательство. Пусть в системе (5) определитель 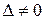 . Обозначим
. Обозначим 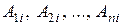 - алгебраические дополнения
- алгебраические дополнения  -го столбца определителя
-го столбца определителя  . Умножим 1-е уравнение системы на
. Умножим 1-е уравнение системы на  , 2-е на
, 2-е на 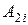 , …,
, …, 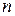 -е - на
-е - на  , и сложим полученные уравнения. В результате получим
, и сложим полученные уравнения. В результате получим
 (10)
(10)
Учитывая, что сумма произведений элементов строки (столбца) на их алгебраические дополнения есть определитель системы, а сумма произведений элементов строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю, получаем, что левая часть (10) равна 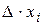 .
.
Несложно заметить, что правая часть (14.6) есть определитель 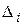 , раскрытый по элементам
, раскрытый по элементам  -го столбца , т.е.
-го столбца , т.е.
 .
.
Таким образом, (14.6) можно записать в виде
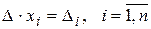 . (11)
. (11)
Откуда, при 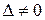 и получаем формулы (9), т.е. формулы Крамера.
и получаем формулы (9), т.е. формулы Крамера.
Замечание. Метод Крамера имеет те же ограничения для применения, что и матричный способ.
Пример 2. Решить систему из примера 1 методом Крамера.
Решение. Вычисляем основной определитель системы:
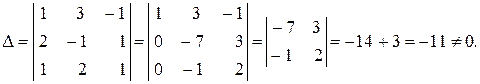
Вычисляем определители 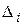 :
:
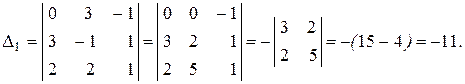

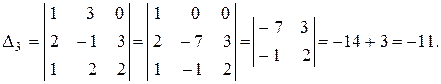
Получаем 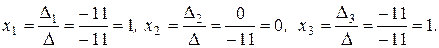
6.
Как было отмечено выше, однородная система линейных уравнений всегда совместна, так как согласно критерия совместности ранги основной и расширенной матрицы совпадают. Это следует из того, что для однородной системы расширенная матрица содержит столбец нулей – столбец свободных членов.
Для того чтобы однородная система имела единственное решение, необходимо и достаточно, чтобы ранг основной матрицы системы был равен числу неизвестных, т.е.  .
.
Единственным решением однородной системы будет нулевое решение. Поэтому для существования ненулевых решений должно выполняться условие 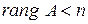 .
.
Если в однородной системе число уравнений равно числу неизвестных, то условие существования ненулевых решений состоит в равенстве нулю основного определителя системы т.е. 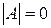 .
.
– Конец работы –
Используемые теги: системы, ных, уравнений, основные, Определения0.081
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Системы линейных уравнений. Основные определения
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов