Теоремы о среднем

 

Теорема Ферма. Пусть f(x) в точке х=а дифференцируема и принима­ет локально максимальное значение, т. е. f(a)>f(x) для всех х из достаточно малой окрестности точки а. Тогда f’(a) =0.

Результат очевиден с разных точек зрения:

Первый вариант. В точке максимального удаления скорость обнуляется — надо остановиться, чтобы двинуться обратно.

Другой вариант. Геометрически понятно, что касательная к локальному максимуму (рис. 3.4) должна быть горизонтальна (tg у = 0).

Третий вариант. В предполо­жении противного, f’(a)>0, например, линейная (самая большая при малом ∆x) часть приращения f(a)∆x > 0 при ∆x > 0, т. е. f(a +∆x) > f(a) при достаточно малых Ах > 0, что противоречит наличию локаль­ного максимума в а.

Обратное, разумеется, неверно. У x³ производная в нуле равна нулю, но нет никакого максимума (в нуле точка перегиба).

Теорема Ролля. Пусть f(x) дифференцируема на [а, b] и f(a) = f(b). Тогда есть точка c[а, b], в которой f’(c) = 0.

Действительно, из того, что f(а) = f(b) вытекает, что f(x) на [а, b] имеет или минимум, или максимум. Далее решает ссылка на предыдущую теорему.

Теорема Лагранжа. Пусть f(x) дифференцируема на [а, b]. Тогда существует точка c(а, b), в которой f’(c). Последнее равенство чаще записывают в виде произведения 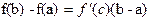, подчеркивая способ выражения ∆f(x) с помощью умножения ∆x на «среднюю скорость роста.