Монотонность, выпуклость, экстремумы

При изучении поведения функции дифференцирование работает весьма эффективно. Основу составляют несколько простых сообра­жений, которые позволяют решать сложные задачи. В этом, кстати, нет противоречия. Элементарные причины могут порождать весьма замысловатые последствия.

Даже такой простой факт, как f '(x) = 0 => f(x) = const, может приносить плоды. Например, для какого-нибудь сложно доказуемого тождества f(x) = g(x) проверка f '(x) = g'(x) может оказаться совсем легкой. Тогда остается убедиться лишь в равенстве f(a) = g(a) и задача решена.

 

Функция f(x) монотонно растет, если 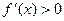, и убывает – если 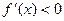. Тоже совсем прозрачный результат. Скорость изменения по­ложительна — функция растет, отрицательна — убывает. Строго положительна — строго растет и т. д. Характер роста f(x) играет важную роль во многих задачах. В случае f'(a) = 0, например, полезно выяснить поведение произ­водной f(x) в окрестности точки а.

Если 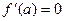и слева от а производная положительна, справа — отрицательна, то у f(x) в точке а — максимум. Если наоборот, то минимум. Производная сохраняет знак — точка перегиба, как у=х³ в нуле.

 

Еще одна полезная категория мышления — выпуклость. Функцию называют выпуклой, когда ее график выглядит, как на рис. 3.5 а, и вогнутой — в случае, изображенном на рис. 3.5 б.

 

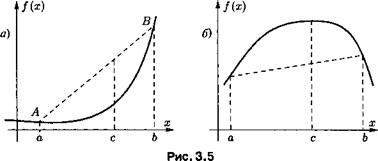
Выпуклая функция с увеличением х растет все быстрее, т. е. скорость f’(x) возрастает (ускорение f’’(x) положительно). Вогнутая функция, наоборот, с увеличением х растет медленнее.

Из рис. 3.5 геометрически ясно, что вертикальный луч, идущий вверх из любой точки с [а, b], пересекает сначала график f(x), потом отрезок AB, что можно записать как

f(pa + qb) < pf(a) + qf(b), при любых неотрицательных р и q, удовлетворяющих условию p+q = 1. Это называют неравенством Йенсена и обычно принимают за определение выпуклой функции, а монотонность производной уже выводят как следствие.

Вообще говоря, выпуклость часто путают с вогнутостью. Поэтому, во избежание недоразумений, многие предпочитают говорить о выпуклости снизу или о выпуклости сверху.

Функцию обычно считают выпуклой, если она имеет выпуклый надграфик, представляющий собой множество точек (x, у), удовлетворяющих неравенству у >f(x).

Достаточно очевидна и возможная роль второй производной 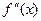(ускорения).

 

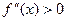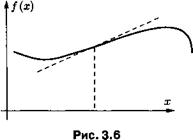
Как уже отмечалось, влечет за собой выпуклость f(x) на соответствующем участке, 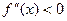—вогнутость. Таким образом, точки, в которых f"(x) обращается в нуль и меняет знак, определяют смену выпуклости на вогнутость (либо наоборот) и классифицируются как точки перегиба. Рис. 3.6 демонстрирует более общий случай, чем х³.