рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ВЕКТОРЫ
Реферат Курсовая Конспект
ВЕКТОРЫ
ВЕКТОРЫ - раздел Математика, КООРДИНАТЫ ТОЧКИ Вектор – Это Направленный Отрезок. Он Задается Длиной И Направлением. Иногда ...
Вектор – это направленный отрезок. Он задается длиной и направлением. Иногда можно прочитать «вектор с началом в точке A и концом в точке B». Это не означает, что у вектора фиксированы начальная и конечная точка. Тот же вектор (с той же длиной и тем же направлением) можно параллельно перенести, и тогда у него будут другие начало и конец. Геометрически конец вектора традиционно обозначают стрелкой.

Векторы, параллельные друг другу, имеющие одинаковые длины, но противоположно направленные, называются взаимно противоположными и при записи различаются знаками.
Для того чтобы задать вектор в пространстве, проще всего поместить его начало в начало координат, тогда координаты конечной точки вектора полностью определят вектор. Поэтому векторы можно задавать с помощью координат.
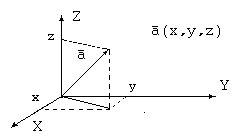
Таким образом, координаты – это проекции вектора на координатные оси. Используя координаты вектора, легко получить его длину (расстояние от конца до начала): 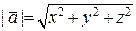 .
.
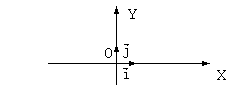
Простейшими векторами в пространстве являются векторы единичной длины, имеющие направления координатных осей. Они называются ортамии обозначаются 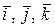 . Эти векторы имеют следующие координаты:
. Эти векторы имеют следующие координаты:  .
.
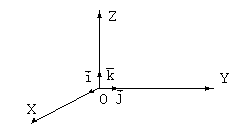
В случае вектора на плоскости XOY используются две координатные оси и каждый вектор имеет две координаты. В этом случае ортами являются векторы  .
.
Кроме того, имеет смысл ввести нулевой вектор  – вектор, имеющий нулевую длину и не имеющий направления.
– вектор, имеющий нулевую длину и не имеющий направления.
1. Линейные преобразования векторов.
Умножение вектора на число. Умножение вектора на положительное число  означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число
означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число  означает умножение длины вектора на число
означает умножение длины вектора на число  и замена направления вектора на противоположное.
и замена направления вектора на противоположное.

При умножении на число координаты вектора умножаются на это число:  .
.
Сложение векторов. Вектор  может быть получен одним из следующих способов.
может быть получен одним из следующих способов.
А) Приставим начало вектора  к концу вектора
к концу вектора 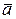 , а затем соединим начало вектора
, а затем соединим начало вектора 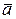 с концом вектора
с концом вектора  . Полученный вектор, конец которого совпадает с концом вектора
. Полученный вектор, конец которого совпадает с концом вектора  и является вектором
и является вектором 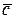 . Очевидно, что результат суммирования не зависит от перестановки слагаемых
. Очевидно, что результат суммирования не зависит от перестановки слагаемых 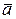 и
и  .
.

Б) Поместим начала векторов 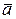 и
и  в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор
в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор  будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов
будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов 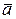 и
и  .
.
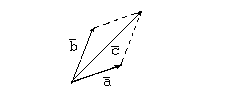
При сложении векторов их соответствующие координаты складываются: если вектор 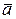 имеет координаты
имеет координаты 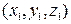 , а вектор
, а вектор  координаты
координаты 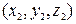 , то вектор
, то вектор  имеет координаты
имеет координаты  . Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству:
. Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству:  .
.
Разложение вектора по базису в трехмерном пространстве и на плоскости. Используя координаты вектора и орты, легко заметить, что вектор 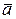 с координатами
с координатами 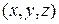 представляет собой следующую линейную комбинацию векторов-ортов:
представляет собой следующую линейную комбинацию векторов-ортов: 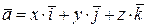 .
.

Такое представление вектора называется разложением вектора по базису, где базисом является набор ортов  . В случае вектора на плоскости XOY базисом является набор
. В случае вектора на плоскости XOY базисом является набор  . В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
. В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
2. Скалярное произведение векторов.
Скалярным произведением двух векторов 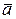 и
и  является число, равное произведению длин векторов на косинус угла между ними:
является число, равное произведению длин векторов на косинус угла между ними:  .
.

Из определения скалярного произведения следует, что  . Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
. Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
Скалярное произведение обладает свойствами: 1) 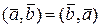 ,
,
2)  .
.
Найдем выражение скалярного произведения с помощью координат. Пусть вектор 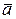 имеет координаты
имеет координаты 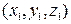 , а вектор
, а вектор  координаты
координаты 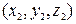 . Их разложения по базису имеют вид
. Их разложения по базису имеют вид 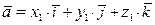 и
и 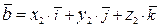 , соответственно. Используя свойства скалярного произведения, получим
, соответственно. Используя свойства скалярного произведения, получим 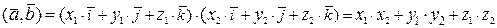 .
.
Используя скалярное произведение двух векторов, легко найти угол между этими векторами. В соответствии с определением скалярного произведения  , следовательно,
, следовательно,
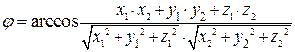 .
.
Условие взаимной перпендикулярности векторов 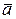 и
и  :
: 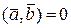 .
.
– Конец работы –
Эта тема принадлежит разделу:
КООРДИНАТЫ ТОЧКИ
Точка на прямой Точка на плоскости Произвольная...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ВЕКТОРЫ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов