АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Прямая. Простейшей плоской кривой является прямая – геометрическое место точек, соединив любые две из которых, мы получим отрезок, параллельный заданному вектору.

Рассмотрим прямую в плоскости XOY. Фиксировать прямую, параллельную данному вектору  с координатами
с координатами 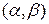 мы сможем, задав одну точку с координатами
мы сможем, задав одну точку с координатами 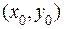 , через которую прямая проходит. Выберем на прямой произвольную точку с координатами
, через которую прямая проходит. Выберем на прямой произвольную точку с координатами  . Тогда из подобия соответствующих треугольников имеем
. Тогда из подобия соответствующих треугольников имеем
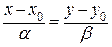 . (1)
. (1)
Соотношение (1) называют каноническим уравнением прямой, оно является основой для получения разных видов уравнения прямой на плоскости. Приравнивая обе части (1) переменной  мы получим параметрическое уравнение прямой:
мы получим параметрическое уравнение прямой:  Вводя угловой коэффициент прямой
Вводя угловой коэффициент прямой  (тангенс угла, образуемого прямой с положительным направлением
(тангенс угла, образуемого прямой с положительным направлением  ), мы получим из (1) уравнение прямой с угловым коэффициентом:
), мы получим из (1) уравнение прямой с угловым коэффициентом: 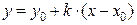 .
.
Приравнивая нулю координаты направляющего вектора  и
и  , получим прямые, параллельные координатным осям:
, получим прямые, параллельные координатным осям:  и
и  .
.
Прямая на плоскости может задаваться не только точкой и направляющим вектором, но и двумя различными точками.

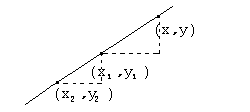
Составляя пропорции сторон подобных треугольников, получим соотношение 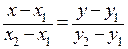 . Это линейное соотношение представляет собой уравнение прямой, проходящей через две различные точки.
. Это линейное соотношение представляет собой уравнение прямой, проходящей через две различные точки.
Частным случаем последнего уравнения является уравнение прямой, проходящей через точки, расположенные на осях координат. Пусть прямая проходит через точки  и
и  . Легко заметить, что ее уравнение принимает вид
. Легко заметить, что ее уравнение принимает вид 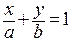 , называемое уравнением прямой в отрезках(имеются в виду отрезки, отсекаемые на осях).
, называемое уравнением прямой в отрезках(имеются в виду отрезки, отсекаемые на осях).