ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА.

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

РАЗДЕЛ. ВВЕДЕНИЕ В АНАЛИЗ.

Действительные числа.

Предметом изучения анализа являются переменные величины (процессы) и соотношения между ними. При этом основываются на понятии числа, которое назовем… Абсолютная величина числа указывает расстояние от точки отсчета до точки, изображающей данное число на оси. Для…

Понятие функции. Общие свойства функции.

Функция является одним из основных понятий математического анализа.

Множество значений аргумента «», для которых задана функция, называется областью определения функции.

Множество значений, которые принимает зависимая переменная, образуют область значений функции.

Функцию можно задать аналитически, указывая алгоритм вычисления значения функции для каждого значения аргумента; табличным способом – записывая перечень всевозможных значений функции с указанием соответствующего аргумента; графически – путем изображения в системе координат множества точек плоскости, координаты которых равны значениям аргумента и функции.

Общие свойства функции.

Четность, нечетность функции.

Функция f называется четной, если:

А) область определения функции симметрична относительно нуля, то есть для любого x, принадлежащего области определения, -x также принадлежит области определения.

б) f(-x)=f(x) для любого x из D(y).

Функция называется нечетной, если:

А) область определения функции симметрична относительно нуля.

б) f(-x)=-f(x) для любого x из D(y).

График четной функции симметричен относительно оси Oy, график нечетной функции симметричен относительно начала координат.

Примеры:

y=cos(x) – четная функция.

y=sin(x) – нечетная функция.

Периодичность.

Число Т называется периодом функции, если f(x)=f(x+T)=f(x-T), где x+T, x-T принадлежат D(y).

Пример.

y=sin(x) – периодическая функция, период .

Пересечение с осями.

(3;0) – точка пересечения с ох.

(0;81) – точка пересечения с оу.

Промежутки знакопостоянства.

f(x)>0 – график функции находится над осью ох.

f(x)<0 – график функции находится ниже оси ох.

Возрастание и убывание.

Функция называется убывающей на промежутке x, если для любых x1 и x2 из этого промежутка таких, что , выполняется неравенство .

Экстремумы функции.

Точка x0 из области определения функции f(x) называется точкой минимума этой функции, если существует такая окрестность точки x0 , что для всех из… Точки максимума и минимума называются точками экстремума, а значения функции в…  

Элементарные функции.Взаимно обратные функции.

Рисунок 1. Графики функций и . С помощью графиков можно находить приближенное решение многих математических задач. Например, корни уравнения…

Область определения функции f совпадает с множеством значений функции g.

Множество значений функции f совпадает с областью определения функции g.

На рисунке 2 показаны графики взаимно обратных функций и . Рисунок 2. Графики функций и

Элементарные функции.

Линейная функция.

Линейной функцией называется функция, которую можно задать формулой вида y=kx+b, где х – независимая переменная, k,b – некоторые числа.

График – прямая.

Прямая пропорциональность – функция, которую можно задать формулой вида y=kx, где х – независимая переменная, k – некоторое число, не равное нулю. График проходит через начало координат.

Степенная функция.

Степенная функция – функция вида f(x)=x^a, где a – постоянное число.

Квадратичной функцией называется функция, которую можно задать формулой вида , где х – независимая переменная, k,b,c – некоторые числа.

Тригонометрическая функция.

Тригонометрические функции – класс элементарных функций: синус, косинус, тангенс, котангенс, секанс, косеканс. Называются также круговыми функциями, так как определение их часто связывают с окружностью единичного радиуса.

А) синус и косинус

Б) тангенс и котангенс

В) секанс, косеканс

Рисунок 3. Тригонометрические функции

Показательная функция.

Показательная функция – функция вида f(x)=a^x.

Рисунок 4. Показательная функция

Логарифмическая функция.

Логарифмическая функция – функция, обратная к показательной функции.

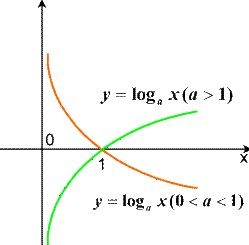
Рисунок 5. Логарифмическая функция

Гиперболические функции.

Гиперболические функции – семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

А) гиперболические синус и косинус

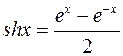
Б) гиперболические тангенс и котангенс

Рисунок 6. Гиперболические функции

Обратные тригонометрические функции.

а) арксинус, арккосинус. б) арктангенс, арккотангенс.

Предел числовой последовательности. Предел функции.

Назовем числовой последовательностью ряд значений функции целочисленного переменного. Если изображать элементы бесконечной последовательности… Понятие предела является удобным инструментом исследования бесконечных… Предел функции непрерывного аргумента.

Вычисление пределов. Виды неопределенностей при вычислении пределов и способы их раскрытия.

Пример. Вычислить . Функция при неограниченно возрастает, следовательно при . Дробь, у которой… Пример. Вычислить .

Способы раскрытия неопределенностей.

Если появляется неопределенность типа то нужно и числитель и знаменатель дроби делить на хк, где к - старшая степень. Если появляется неопределенность типа то нужно стремиться разложить на множители числитель и знаменатель, выделяя…

Первый замечательный предел

Следствия:

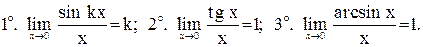
Второй замечательный предел

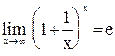или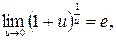

где число е - иррациональное, е 2,71828...

Следствия:

(1^¥)

Неопределенность (1^¥) раскрывается с помощью второго замечательного предела.

 

Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов функций

  Так как , то при - бесконечно малая. Однако cos(x) не является бесконечно… Две бесконечно малые называются эквивалентными, если предел их отношения равен 1.

Основные формулы эквивалентности бесконечно малых.

При . (1)

Понятие непрерывности функции и точки разрыва

Функция непрерывна на интервале , если она непрерывна в каждой точке этого интервала. Элементарные функции непрерывны во всех точках, в которых они определены. Рассмотрим примеры функций, имеющих точки, в которых не выполняется определение непрерывности. Такие функции называют…

РАЗДЕЛ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ.

Производная функции. Геометрический смысл производной.

Понятие производной встречается при решении многих математических и физических задач и является важной характеристикой функции. Геометрический смысл производной: производная равна тангенсу угла наклона…  

Основные правила дифференцирования. Таблица производных.

1. 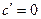, с – const.

2.

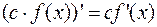
3.

4.

5.

Таблица производных основных элементарных функций.

1. ;

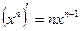2. ;

3. ;

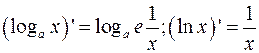4. ;

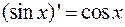5. ;

6. ;

7. ;

8. ;

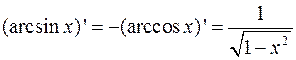9. ;

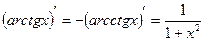10. ;

11. ;

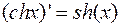12. ;

13. .

 

Производная сложной функции. Производная обратной функции. Производные высших порядков.

Правило дифференцирования сложной функции: . Для монотонной функции существует обратная функция . Если функция… Производную функции в свою очередь можно дифференцировать. В результате получим производную второго порядка .…

Производная неявно заданной функции. Логарифмическое дифференцирование, дифференцирование функций, заданных параметрически.

  Найти производную функции в точке А. , .

Дифференциалы первого и высших порядков и их приложение.

Проведем к графику функции касательную (см. рис.10).

Рисунок 10.

Используем касательную для приближенного вычисления приращения функции .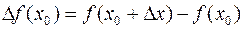

Касательная имеет уравнение .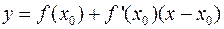

Отсюда при находим

.

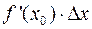Символ "~" обозначает приближенное равенство при малых .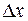

Выражение в правой части формулы называется дифференциалом функции и обозначается

.

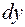
Правила нахождение дифференциалов.

1. d(С)=0 (С –const);

2. dx=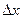, если х – независимая переменная;

3. ;

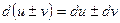4. ;

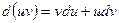5. d(Cu)=Cdu;

6. , .

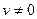Дифференциалом n-го порядка функции f(x) называется дифференциал от дифференциала (n-1)-го порядка этой функции.

.

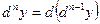
Формула 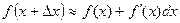применяется для приближенного вычисления значений функции.

 

Теоремы о среднем. Правило Лопиталя-Бернулли.

1) Теорема Ролля: если , то непременно существует точка , в которой . 2) Теорема Лагранжа: На интервале непременно существует точка , в которой . … 3) Теорема о возрастании и убывании функции: Если на интервале , то на этом интервале функция монотонно возрастает;…

Правило Лопиталя-Бернулли.

Правило Лопиталя-Бернули справедливо также для случая, когда . Пример.

Уравнение касательной, уравнение нормали.

y-y0=f/(x0)×(x-x0). Уравнение нормали к кривой y=f(x) в точке х0 имеет вид

Наибольшее и наименьшее значение функции на отрезке.

1. Найти критические точки. Определить какие из них принадлежат заданному отрезку. 2. Вычислить значение функции в критических точках и на концах отрезка. 3. Выбрать среди найденных значений функции наибольшее и наименьшее.

Приложение производной к исследованию функций и построению графиков. Монотонные функции.

Функция называется возрастающей на промежутке x, если для любых x₁ и x₂ из этого промежутка таких, что 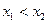, выполняется неравенство .

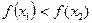Функция называется убывающей на промежутке x, если для любых x₁ и x₂ из этого промежутка таких, что 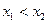, выполняется неравенство .

Функция, возрастающая в интервале или убывающая в интервале, называется монотонной в этом интервале.

Признаки возрастания функции.

Если непрерывная на отрезке [a,b] и дифференцируемая внутри него функция…

Приложения производной к исследованию функций и построению графиков. Экстремумы.

Экстремумом функции называют ее минимальное или максимальное значение.

Определение минимума (максимума): непрерывная функция имеет в точке 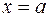минимум или максимум, если в достаточно малой окрестности этой точки (слева и справа от нее) все значения функции больше минимального 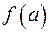, и все значения функции меньше 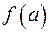в случае, когда 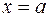– точка минимума.

На графике точка экстремума соответствует впадине (минимум) или выступу (максимум). Понятие экстремума относится только к некоторой ограниченной области. Вне ее функция может принимать значения больше максимального или меньше минимального. В связи с этим наряду с экстремумом вводится понятие наибольшего и наименьшего значения функции, как самого большого и самого малого, которые принимает функция на некотором интервале. Наибольшее и наименьшее значение функции выбираются среди ее экстремальных значений и значений на границах интервала.

В точке экстремума касательная к графику функции горизонтальна. Отсюда следует необходимый признак экстремума: если в точке экстремума производная функции существует, то она равна нулю. Однако равенство нулю производной не гарантирует наличие экстремума (необходимый признак не является достаточным). Например, производная функци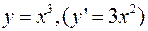и при 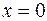обращается в нуль, но экстремума в этой точке нет.

Рисунок 11.

Полностью вопрос об экстремумах решается с помощью необходимого и достаточного признака существования экстремума: функция имеет в точке 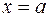экстремум, если производная 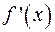меняет знак при переходе через эту точку; экстремум является минимумом при изменении знака производной с (-) на (+) и максимумом при изменении знака с (+) на (-).

Пример:

1. Исследовать на экстремум функцию

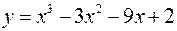
Дифференцируем функцию и отыскиваем нули ее производной

,

,

,

,

.

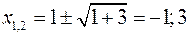Исследуем знак производной:

на интервале 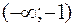будет ,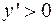

-

-

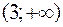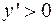
Отсюда при 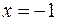функция имеет максимум 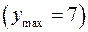; при - минимум .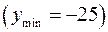

Задачи на отыскание наименьших и наибольших значений.

Рассмотренный метод отыскания экстремальных значений функции широко применяется при решении прикладных задач, в которых требуется отыскать наибольшее или наименьшее значение какого-нибудь параметра.

 

Приложения производной к исследованию функций и построению графиков. Выпуклость, вогнутость, точки перегиба.

Вогнутость кривой

Кривая называется вогнутой вверх в точке 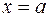, если она лежит выше своей касательной, и вогнутой вниз - если ниже. Направление вогнутости кривой аналитически определяется по закону второй производной посредством признака вогнутости: если на интервале 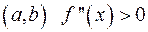, то при этом интервале кривая вогнута вверх; при кривая вогнута вниз.

Точка кривой, в которой происходит изменение направления вогнутости, называют точкой перегиба. Признаком существования точки перегиба является изменение знака второй производной при переходе через эту точку. Точки перегиба отыскиваются среди нулей и точек разрыва .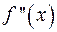

По направлению вогнутости кривой можно определить характер экстремума функции: если 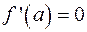, то в точке 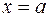функция имеет минимум, если 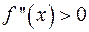, и максимум, если .

Данный признак является следствием того, что в точке максимума график функции вогнут вниз, а в точке минимума вверх.

Пример: Исследовать на экстремум функцию .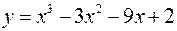

Эта функция имеет производную , которая обращается в нуль в точках 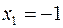и 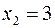. Вторая производная функции равна 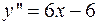. При этом и 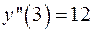. Согласно вышеуказанному признаку при 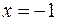функция имеет максимум, а при - минимум.

 

Приложения производной к исследованию функций и построению графиков. Асимптоты графика функции.

Асимптотой называют прямую, к которой неограниченно близко приближается график функции. Асимптоты характеризуют поведение функции при больших значениях аргумента или функции и удобны при построении графиков.

По методу нахождения различают вертикальные и наклонные асимптоты.

Вертикальную асимптоту функция имеет в том случае, если у нее есть точка бесконечного разрыва 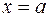. Уравнение вертикальной асимптоты будет .

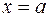Наклонная асимптота имеет уравнение .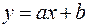

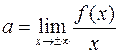и .

Пример. Найти асимптоты графика функции

В точке функция имеет точку бесконечного разрыва, поэтому уравнение вертикальной асимптоты будет . Определим теперь коэффициенты уравнения наклонной асимптоты:

.

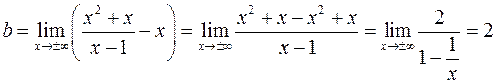Таким образом, наклонная асимптота имеет уравнение .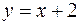

 

Приложение производной к исследованию функций и построению графиков. Общая схема исследования.

Общая схема исследования.

1. Область определения. Точки разрыва.

2. Четность, нечетность.

3. Периодичность.

4. Интервалы знакопостоянства.

5. Интервалы возрастания, убывания, экстремумы.

6. Интервалы выпуклости, вогнутости, точки перегиба.

7. Асимптоты.

8. Дополнительные точки.

Пример. Исследовать функцию и построить ее график.

1. Устанавливаем область определения функции, находим точки разрыва, исследуем поведении функции в окрестности этих точек, а также на границах области определения.

Заданная функция определена на всей действительной оси за исключением точек 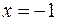и , в которых она имеет разрыв. При приближении к этим точкам функция неограниченно возрастает. Поэтому прямые 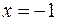и являются вертикальными асимптотами функции. При неограниченном возрастании или убывании функция стремится к .

2. Исследуем функцию на четность и нечетность, определяем интервалы знакопостоянства функции.

Функция четна, так как 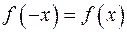, ее график симметричен относительно оси ординат.

3. Функция не имеет периода.

4. Для исследования знака функции разбиваем область ее определения на интервалы точками, в которых она обращается в нуль или имеет разрыв, и определяем знак функции в каждом из этих интервалов. На интервалах 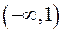и функция отрицательна; на интервале 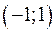- положительна. При переходе через нуль функции (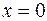) функция знака не меняет, следовательно, прямая 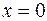касается графика функции в точке .

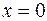5. Исследовав первую производную, определяем интервалы возрастания и убывания функции, находим точки экстремума.

Производная функции равна

.

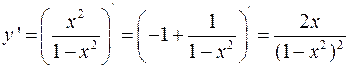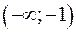Функция изменяет знак только при переходе через точки, в которых она обращается в нуль или имеет разрыв. Поэтому знак производной определяем в каждом из следующих интервалов: и . Находим: в интервалах и - ; в интервалах и - 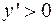. Следовательно, в двух первых интервалах функция убывает, а в последних - возрастает. При 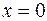производная функции обращается в нуль, и при переходе через эту точку производная меняет знак с (-) на (+). Поэтому в точке 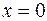функция имеет минимум - .

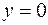6. Изучив вторую производную, находим интервалы вогнутости вверх и вниз графика функции, определяем точки перегиба.

Вторая производная функции равна

.

Она отрицательна при и положительна при . Поэтому на интервалах и график функции вогнут вниз, а на интервале 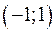- вверх. Вторая производная нигде не обращается в нуль (функция, стоящая в числителе, всегда положительна), и поэтому график не имеет точек перегиба.

7. Находим наклонные и горизонтальные асимптоты функции.

Функция имеет:

горизонтальную асимптоту y = -1;

вертикальные асимптоты x = -1; x = 1.

Проведенное исследование устанавливает общий характер изменения функции и позволяет построить ее график. Построение графика рекомендуется начать с проведения асимптот и отметки точек, в которых функция и ее две производные или обращаются в нуль, или имеют точки разрыва. График исследованной функции изображен на рис.12.

Рисунок 12.