Взаимное расположение двух плоскостей. Угол между плоскостями. Расстояние от точки до плоскости.
Рассмотрим плоскости  и
и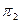 , заданные своими общими уравнениями:
, заданные своими общими уравнениями:
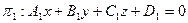 ;
;
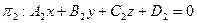 .
.
 и
и 
r – ранг основной матрицы;
R – ранг расширенной матрицы.
Возможны три случая взаимного расположения двух плоскостей:
1) плоскости параллельны, но не совпадают (r=1, R=2);
2) плоскости совпадают (r=1,R=1);
3) плоскости не параллельны, т.е. пересекаются по прямой (r=2).
Частым случаем является перпендикулярность двух плоскостей.
Для случаев 1) и 2) общим является то, что векторы 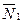 и
и 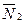 коллинеарны.
коллинеарны.
Угол между плоскостями – это один из смежных двугранных углов, образованных этими плоскостями.
Углом между двумя плоскостями и
и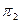 называется угол
называется угол  между нормальными векторами этих плоскостей .
между нормальными векторами этих плоскостей .
Нормальный вектор 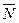 к данной плоскости может иметь любое из двух противоположных друг другу направлений, поэтому угол между плоскостями определен неоднозначно : для угла
к данной плоскости может иметь любое из двух противоположных друг другу направлений, поэтому угол между плоскостями определен неоднозначно : для угла  возможны два варианта записи:
возможны два варианта записи:  и
и  . Учитывая, что
. Учитывая, что  можно косинус угла между плоскостями находить по формуле:
можно косинус угла между плоскостями находить по формуле:
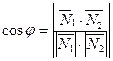 , где
, где 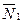 и
и 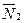 любые два вектора, перпендикулярные плоскостям
любые два вектора, перпендикулярные плоскостям  и
и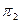 или
или 
Условие параллельности двух плоскостей. Если плоскости  и
и 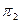 параллельны, то их нормальные вектора коллинеарные. Признаком колленеарности двух векторов является пропорциональность их координат.
параллельны, то их нормальные вектора коллинеарные. Признаком колленеарности двух векторов является пропорциональность их координат.
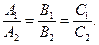
Условие перпендикулярности двух плоскостей. Плоскости  и
и 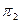 перпендикулярны, следовательно, их нормальные вектора перпендикулярны
перпендикулярны, следовательно, их нормальные вектора перпендикулярны ^
^  . Признаком перпендикулярности двух векторов является равенство нулю их скалярного произведения. A1A2 + B1B2 + C1C2 = 0.
. Признаком перпендикулярности двух векторов является равенство нулю их скалярного произведения. A1A2 + B1B2 + C1C2 = 0.
Расстояние от точки до плоскости
Пусть дана точка  и плоскость
и плоскость 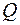 :
:  . Расстояние
. Расстояние 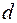 между ними, то есть длина перпендикуляра, опущенного из точки
между ними, то есть длина перпендикуляра, опущенного из точки  на плоскость
на плоскость 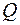 :
:  определяется аналогично расстоянию от точки до прямой.
определяется аналогично расстоянию от точки до прямой.