Определители третьего порядка, определители высших порядков.
Рассмотрим матрицу порядка 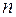 .
.
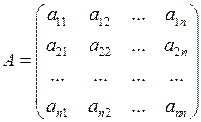 .
.
Возьмем произвольный элемент 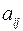 этой матрицы
этой матрицы 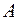 , удалим ту строку и тот столбец, на пересечении которых стоит этот элемент (т.е.
, удалим ту строку и тот столбец, на пересечении которых стоит этот элемент (т.е.  -ую строку и
-ую строку и  -ый столбец). Тогда получим матрицу
-ый столбец). Тогда получим матрицу 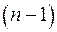 -го порядка. Определитель этой матрицы
-го порядка. Определитель этой матрицы 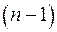 -го порядка называется минором матрицы
-го порядка называется минором матрицы 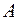 , соответствующим элементу
, соответствующим элементу 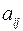 , и обозначается
, и обозначается  .
.
Пусть исходная матрица была 3-го порядка: 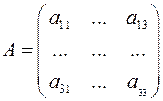 .
.
Она имеет девять миноров, являющихся определителями матриц 2-го порядка.
Запишем минор  ,
,  и т.д.
и т.д.
 ,
, 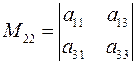 и так далее.
и так далее.
Определение:определителем матрицы 3-го порядка называется число, вычисляемое по следующему правилу:

Эта формула называется разложением определителя матрицы по элементам первой строки.
Так как свойства определителя матрицы 2-го порядка верны и для определителей матриц 3-го порядка и высших порядков, то, учитывая 1-ое свойство, можно записать разложение определителя матрицы по элементам первого столбца:
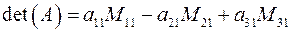 .
.
А учитывая 2-ое свойство (при перестановке двух строк (или столбцов) матрицы значение определителя матрицы не меняется, а знак меняется на противоположный), можем записать разложение определителя матрицы по элементам любой строки


и столбца

 .
.
Определение:Алгебраическим дополнением элемента 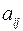 матрицы
матрицы 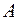 называется минор
называется минор  этой матрицы, взятый со знаком плюс, если сумма
этой матрицы, взятый со знаком плюс, если сумма 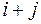 четна и минус, если
четна и минус, если 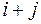 – нечетна.
– нечетна.
 ,
,  ,
, 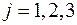 .
.
Теперь формулы для вычисления определителя матрицы через его миноры можно записать так:
 ,
,
 ,
,
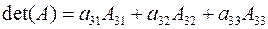 ,
,
 ,
,
 ,
,
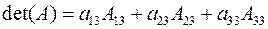 .
.
Пусть дана матрица 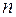 -го порядка
-го порядка
 .
.
Определителем этой матрицы называется число, полученное по следующему правилу:
 , (2)
, (2)
причем  , а минор
, а минор  будет определителем матрицы
будет определителем матрицы 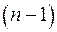 -го порядка.
-го порядка.
Формула (2) есть разложение определителя по элементам первой строки.
Все свойства верны для матриц 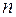 -го порядка.
-го порядка.