Метод Гаусса (приведение к ступенчатому виду).

Численное решение системы линейных алгебраических уравнений порядка 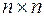с помощью определителей удобно производить для систем двух и трех уравнений. В случае же систем большего числа уравнений гораздо выгоднее пользоваться методом Гаусса, который заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе четырех уравнений с четырьмя неизвестными:

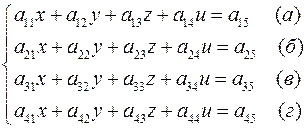
Допустим, что 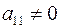(если 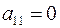, то изменим порядок уравнений, выбрав первым такое уравнение, в котором коэффициент при 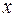не равен нулю).

I шаг: делим уравнение (а) на 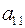, умножаем полученное уравнение на 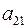и вычитаем из (б); затем умножаем на 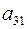и вычитаем из (в); наконец, умножаем на 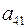и вычитаем из (г). В результате I шага приходим к системе:

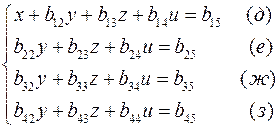
Причем 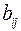получаются из 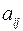по следующим формулам:

; .

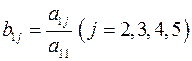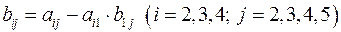II шаг: поступаем с уравнениями (е), (ж), (з) точно так же, как с уравнениями (а),(б), (в), (г) и так далее. В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.

Теорема 1. Система линейных уравнений несовместна тогда и только тогда, когда в ее ступенчатом виде имеется уравнение 0 = b_t, где b_t не равно 0.

Система линейных уравнений может иметь главные переменные и свободные переменные.

Выражение главных переменных через свободные переменные называется общим решением системы.

Решение, полученное при заданных значениях свободных переменных называется частным решением.

Теорема 2.Система линейных уравнений совместна и неопределенна тогда, когда система ее ступенчатого вида совместна и имеет свободные переменные.

Теорема 3.Совместная система линейных уравнений имеет единственное решение тогда, когда в ее ступенчатом виде нет свободных переменных, то есть все переменные главные.