рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Связь сферической системы координат с
Реферат Курсовая Конспект
Связь сферической системы координат с
Связь сферической системы координат с - раздел Математика, КУРС ВЫСШЕЙ МАТЕМАТИКИ Декартовой Прямоугольной. В Случае Сферическо...
декартовой прямоугольной.
В случае сферической системы координат соотношения имеют вид:


Линейное (векторное) пространство.
Как известно, линейные операции (сложение, вычитание, умножение на число) определены по-своему для каждого множества (числа, многочлены, направленные отрезки, матрицы). Сами операции различны, но их свойства одинаковы.
Эта общность свойств позволяет обобщить понятие линейных операций для любых множеств вне зависимости от того, что это за множества (числа, матрицы и т.д.).
Для того, чтобы дать определение линейного (векторного) пространства рассмотрим некоторое множество L действительных элементов, для которых определены операции сложения и умножения на число.
Эти операции обладают свойствами:
1) Коммутативность  +
+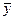 =
= 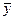 +
+
2) Ассоциативность ( +
+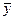 ) +
) +  =
=  + (
+ (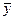 +
+ )
)
3)Существует такой нулевой вектор 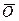 , что
, что 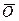 +
+ =
= для "
для " Î L
Î L
4) Для " Î L существует вектор
Î L существует вектор 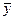 = -
= - , такой, что
, такой, что  +
+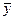 =
=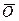
5)1× =
= 
6) a(b ) = (ab)
) = (ab)
7) Распределительный закон (a + b) = a
= a + b
+ b
8) a( +
+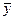 ) = a
) = a + a
+ a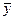
Определение: Множество L, элементы которого обладают перечисленными выше свойствами, называется линейным (векторным) пространством, а его элементы называются векторами.
Важно не путать понятие вектора, приведенное выше с понятием вектора как направленного отрезка на плоскости или в пространстве. Направленные отрезки являются всего лишь частным случаем элементов линейного (векторного) пространства. Линейное (векторное) пространство – понятие более широкое. Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.
Свойства линейных пространств.
1) В каждом линейном пространстве существует только один нулевой элемент.
2) Для каждого элемента существует только один противоположный элемент.
3) Для каждого  Î L верно 0×
Î L верно 0× = 0
= 0
4) Для каждого a Î R и 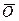 Î L верно a×
Î L верно a×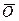 =
=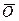
5) Если a× =
= 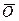 , то a = 0 или
, то a = 0 или  =
= 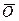
6) (-1)  = -
= -
Линейные преобразования.
Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу  Î L по некоторому правилу ставится в соответствие элемент А
Î L по некоторому правилу ставится в соответствие элемент А Î L.
Î L.
Определение: Преобразование А называется линейным, если для любых векторов  Î L и
Î L и 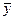 Î L и любого a верно:
Î L и любого a верно:
A( +
+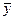 ) = A
) = A +A
+A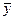
A(a ) = aA
) = aA
Определение: Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя.
Е =
= 
Пример. Является ли А линейным преобразованием. А =
= +
+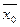 ;
; 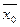 ¹ 0.
¹ 0.
Запишем преобразование А для какого- либо элемента 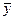 . А
. А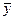 =
= 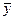 +
+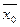
Проверим, выполняется ли правило операции сложения для этого преобразования А( +
+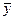 ) =
) = 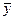 +
+ +
+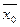 ; A(
; A( ) + A(
) + A(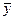 ) =
) =  +
+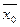 +
+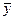 +
+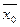 , что верно только при
, что верно только при 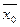 = 0, т.е. данное преобразование А нелинейное.
= 0, т.е. данное преобразование А нелинейное.
Определение: Если в пространстве L имеются векторы линейного преобразования 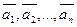 , то другой вектор
, то другой вектор 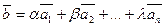 является линейной комбинацией векторов
является линейной комбинацией векторов 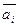 .
.
Определение: Если 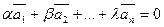 только при a = b = … = l = 0, то векторы
только при a = b = … = l = 0, то векторы 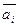 называются линейно независимыми.
называются линейно независимыми.
Определение: Если в линейном пространстве L есть n линейно независимых векторов, но любые n + 1 векторов линейно зависимы, то пространство L называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L.
Следствие: Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса.
Матрицы линейных преобразований.
Пусть в n- мерном линейном пространстве с базисом  ,
, ,…,
,…, задано линейное преобразование А. Тогда векторы А
задано линейное преобразование А. Тогда векторы А ,А
,А ,…,А
,…,А - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
A = a11
= a11 + a21
+ a21 +…+ an1
+…+ an1
A = a12
= a12 + a22
+ a22 +…+ an2
+…+ an2
……………………………….
A = an1
= an1 + an2
+ an2 +…+ ann
+…+ ann
Тогда матрица А =  называется матрицей линейного преобразования А.
называется матрицей линейного преобразования А.
Если в пространстве L взять вектор  = x1
= x1 + x2
+ x2 +…+ xn
+…+ xn , то A
, то A Î L.
Î L.
 , где
, где
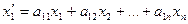

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе  ,
, ,…,
,…, .
.
В матричном виде:
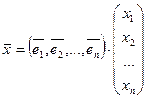 , А×
, А×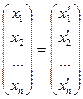 ,
, 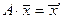
Пример. Найти матрицу линейного преобразования, заданного в виде:
– Конец работы –
Эта тема принадлежит разделу:
КУРС ВЫСШЕЙ МАТЕМАТИКИ
mailto aalar yandex ru... К У Р С В Ы С Ш Е Й М А Т Е М А Т И К И...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Связь сферической системы координат с
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов