ОСНОВИ ДИСКРЕТНОЇ МАТЕМАТИКИ

Міністерство освіти і науки України
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
Інститут комп’ютерних систем

О.М. Мартинюк

ОСНОВИ ДИСКРЕТНОЇ МАТЕМАТИКИ
КОНСПЕКТ ЛЕКЦІЙ
для студентів очної та заочної форм навчання
напрямку 6.0804 і 6.0915

Затверджено
на засіданні вченої ради ОНПУ,
протокол № 1 від 31.08.04

ОДЕСА
Наука і техніка
2006

Рецензенти:
О.В. Дрозд, д.т.н., професор,
О.Б. Кунгурцев, к.т.н., доцент

 

Мартинюк О.М. Конспект лекцій з дисципліни «Основи дискретної математики» для студентів очної і заочної форм навчання напрямку 6.0804 і 6.0915. – Одеса: Наука і техніка, 2006. – 225 с.

 

Конспект лекцій з дисципліни «Основи дискретної математики» містить виклад основних визначень, операцій і властивостей п’яти базових розділів дискретної математики – теорії множин і алгебраїчних систем, комбінаторики, графів, скінченних автоматів та булевої алгебри, і є орієнтованим на прикладні задачі комп'ютерних спеціальностей.

Наука і техніка, 2006

Вступ

Підвищенню рівня математичної підготовки студентів вузів, що особливо спеціалізуються в галузі комп'ютерних систем і мереж, традиційно приділяється велика увага. Особливе значення в цьому плані має вивчення сучасних розділів математики, таких як теорія множин, булева алгебра, теорії графів і автоматів, що є математичною основою для цілого ряду спеціальних дисциплін кібернетичного циклу. Ці розділи заведено відносити до дискретної математики, яка є базою кібернетики.

Запропонований конспект лекцій з дисципліни «Основі дискретної математики» підготовлений відповідно до програми дисципліни, що вивчається студентами інституту комп'ютерних систем ОНПУ. Необхідність видання конспекту обумовлена тим, що склад розділів навчальних посібників, присвячених дискретній математиці і призначених для студентів технічних вузів, не відповідає специфіці викладання в ОНПУ. Даний конспект має за мету дати студенту матеріал для самостійної роботи і більш глибокого засвоєння специфічних математичних знань, а також полегшити викладачам підготовку до проведення занять.

До конспекту включені розділи теорії множин і алгебраїчних систем, комбінаторики, графів, скінченних автоматів і булевої алгебри. Третій і четвертій розділи представлені у вступній формі в зв'язку зі спеціальним, більш вузьким і прикладним їх вивченням у наступних дисциплінах. Конспект викладений з послідовним ускладненням матеріалу, ілюстрований необхідними прикладами та оформлений у вигляді тридцяти шести лекцій, що містять кілька параграфів, супроводжуються вступом, змістом, контрольними запитаннями і літературою. Кожен параграф містить необхідні теоретичні відомості, що являють основні поняття, визначення, операції і властивості. Перелік літератури, що наводиться, не претендуючи на вичерпну повноту, містить навчальні посібники і книги, Якіми може скористатися студент.

У літературі в галузі термінології і позначень є різночитання. У конспекті використовується термінологія і позначення, що прийняті у першоджерелах [1-6] - розділ 1; [2, 3] - розділ 2, [1, 2, 3, 6, 10] – розділ 3, [1, 2, 5, 6, 7, 12] – розділ 4, [1, 2, 4, 6-9] – розділ 5.

Для самостійного вивчення теорії рекомендуються першоджерела: до розділу 1 - [1-3, 5] - основні, [4-6, 12]- додаткові; до розділу 2 - [3] - основні, [1] - додаткові; до розділу 3 - [1, 2, 10]- основні, [11] – додаткові; до розділу 4 - [2, 7, 12]- основні, [11] – додаткові. ; до розділу 5 - [1, 9] - основні, [8, 14] – додаткові. Більш докладний матеріал для практики (і для самостійної роботи взагалі) можна знайти в першоджерелах [20-23].

розділ 1. ТЕОРІЯ МНОЖИН І АЛГЕБРАЇЧНИХ СИСТЕМ

Лекція 1. Основні поняття теорії множин

Вступ

Лекція має за мету навести початкові поняття з теорії множин. Розглянуто основні визначення множин та п’яти операцій, існуючі базові вісімнадцять тотожностей і засоби їх доведення. Звернено повагу до узагальнення властивостей множин та операцій і принципу подвійності.

Лекція містить чотири підрозділи:

1.1. Основні поняття і завдання множин

1.2. Операції над множинами. Формули. Тотожності

1.3. Доведення тотожностей. Булева алгебра множин

1.4. Узагальнення операцій. Подвійність

1.1. Основні поняття і завдання множин

Визначення. Під множиною розуміється об'єднання визначених, відмінних один від одного об'єктів (реальних чи уявлюваних), що називають елементами множини в їхній сутності.

Приклад. А={ 1,2,а,b} - коректно, В={ а,b,c,b} - некоректно.

Загальне позначення множин - фігурні дужки {...}, усередині яких задаються елементи множин. Конкретні множини позначаються великими літерами А, В₄, С_і, ..., елементи множин позначаються рядковими латинськими літерами a, b₄, сі ... .

Запис mÎM означає висловлення «m є елементом множини М» чи «m належить множині М». Запис mÏM означає заперечення висловлення mÎM.

Запис М₁ÍМ₂ означає висловлення «кожен елемент множини М₁ є елементом множини М₂», чи «M₁ є підмножиною множини М₂, а М₂ – надмножиною множини М₁», чи «M₁ міститьться в М₂».

Запис М₁ËМ₂ - заперечення висловлення М₁ÍМ₂.

Запис М₁=М₂ означає висловлення «M₁ÍM₂ і М₂ÍМ₁» чи «множини М₁ і М₂ рівні (еквівалентні)».

Запис М₁¹М₂ - заперечення висловлення М₁=М₂.

Запис М₁ÌМ₂ еквівалентний висловленню «M₁ÍM₂ і М₁¹М₂» чи «M₁ є власною підмножиною множини М₂». Невласні множини в цьому випадку - сама множина М₂ і множина Æ - єдина множина, що не містить елементів - порожнє М.

Можна вважати, що всі розглянуті множини є підмножинами деякого універсуму U (для цілих чисел - нескінченність).

Визначення. Множина, елементами якої є всі підмножини множини М, називається множиною підмножин, чи множиною-ступенем, чи булеаном множини М і позначається як Р(М) чи В(М).

Приклад. М={1,2,3}, P(M)={Æ, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.

Запис |М| означає число елементів множини М, |Р(М)|= 2^|М|.

Завдання множин здійснюється трьома основними способами:

1. Приклад:Перерахування всіх елементів, що входять у множину.

Приклад. А={а₁, а₂, а₃ }, B={1, 2, b, c}, C={а_і}₁ ³

2. Завданням характеристичної властивості, що виділяє елементи даної множини серед елементів, що зазначені іншим множинам.

Приклад. N={n|nÎZ і n>0}, М={mÎM|m=n² і nÎN}

3. Описом процедури, що породжує, із зазначенням множин, що пробігають параметри цієї процедури.

Приклад. М={n²|nÎN}, C ={8х₁+14х₂+32х₃|х₁, х₂, х₃ÎZ}.

З визначення рівності множин і способів завдання їх випливає, що порядок елементів у множинах несуттєвий.

Для інтерпретації множин і операцій над ними використовуються геометричні фігури - кола Ейлера і діаграми Венна (рис. 1.1.).

 

Рис. 1.1. Кола Ейлера

1.2. Операції над множинами. Формули. Тотожності

Нові множини породжуються в результаті застосування операцій до існуючих множин.

Об'єднанням множин М₁ і М₂ називається множина М₁ÈM₂={m|mÎM₁ чи mÎM₂}.

Перетином множин М₁ і М₂ називається множина М₁ÇM₂={m|mÎM₁ і mÎM₂}.

Множини М₁ і М₂ називаються диз'юнктними, якщо М₁ ÇM₂=Æ.

Різниця множин М₁ і М₂ - це множина М₁М₂={m|mÎM₁ і mÏM₂}.

Симетричною різницею множин М₁ і М₂ називається множина
М₁-М₂= {m|mÎM₁M₂ чи mÎМ₂М₁}.

Якщо М₁ÍM₂, то різниця М₂М₁ називається доповненням
множини М₁ у множині М₂. Зокрема, `М = UM - доповнення множини М в універсумі чи просто доповнення множини М. Інше позначення доповнення множини - ùМ.

Приклад. A={1,2, 3, 4}; B={3, 4 5}; З ={1, 3}; AÈB={1, 2, 3 , 4, 5}; AÇB={3, 4}; AЗ ={2, 4}; AB={1, 2}; BA={5}; A-B={1,2,5}.

Теорема. Будь-які дві множини А і В можуть знаходитися в одному з п'яти станів: 1)А=В; 2)АÌВ; 3)АÉВ; 4)АÇВ=Æ; 5)АВ ¹Æ і ВА¹Æ і АÇВ¹Æ

Завдання нових множин за допомогою ідентифікаторів, операцій і дужок, тобто завдання за допомогою формул називається аналітичним.

Для операцій над множинами справедливі закони (тотожності):

1. AÈB=BÈA; AÇB=BÇA; комутативність

2. AÈ(BÈЗ)=(AÈB)ÈЗ; AÇ(BÇЗ)=(AÇB)ÇC; асоціативність

3. AÈ(BÇC)=(AÈB)Ç(AÈC); AÇ(BÈC)=(AÇB)È(AÇC);

Дистрибутивність

5. AÈ`A=U; AÇ`A=Æ; доповнення 6. AÈA=A; AÇA=A; ідемпотентність 7. AÈ(AÇB)=A; AÇ(AÈB)=A; поглинання

М1ÈM2ȼÈМn=È{Мі|1£ і £ n}={m| існує і, де 1£і£n, таке, що mÎMі}.

М1ÇM2ǼÇMn=Ç{Mі|1£ і £ n}={m| для кожного і., де 1£ і£n, виконане mÎMі}.

М1-M2-¼-Mn=-{Mі|1 £ і £ n }={m| існує і єдино і, де 1£і£n, таке, що mÎMі}.

È{Mі|MіÎM і Мі задовольняє умову В}. Приклад. È{Mі|MіÎB(Z) і MіÇN0=Æ} - множина усіх… Замість È{Mі|іÎN} використовується запис ÈMі . Аналогічно - для ¢¢Ç¢¢ і…

Контрольні запитання

2. Які способи завдання множин існують? 3. Які операції діють над множинами? 4. Як можуть співвідноситися дві множини?

Основна

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатом-издат, 1987. - С.24-44. Додаткова 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.86-97.

Вступ

Лекція має за мету поширити використання теорії множин. Розглянуто розв’язання рівнянь, що містять фіксовані підмножини і підмножини, що полягають визначенню, покриття і розбивки не порожньої множини, а також скінченні і нескінчені множини. Звернуто повагу до базового алгоритму розв’язання рівнянь, понять блоків, або класів, потужності множин і кардинальних чисел.

Лекція містить три підрозділи:

2.1. Рівняння

2.2. Покриття і розбивки

2.3. Потужність множин. Зчисленні і континуальні множини.

2.1. Рівняння

Алгебра множин поряд з тотожностями розглядає і рівняння, що містять фіксовані підмножини універсуму і підмножини універсуму, що підлягають визначенню. Потрібно визначити, при яких умовах рівняння має розв’язання і яке саме. Розв’язання рівнянь з однією обумовленою підмножиною ґрунтується на таких тотожних перетвореннях:

1. Відповідно до тотожності 18 рівність перетвориться в симетричну різницю його лівої і правої частин, що прирівнюється (.

2. Отримане рівняння перетвориться до вигляду (MÇX)È(NÇ`X)=Æ де М и N деякі множини, що не містять Х.

3. Тому що об'єднання множин порожньо, якщо кожне з поєднуваних множин порожнє, перетворене в п.2 рівняння можна замінити системою двох рівнянь МÇC=Æ і NÇ`C=Æ.

4. Відповідно до тотожності 17 пари рівнянь п.3 мають сенс тоді і тільки тоді, коли NÌC і CÌ`M. Значить умова існування розв’язання - NÌ`M, а розв’язання рівняння - будь-яка множина Х така, що NÌCÌ`M.

Приклад. CÈС=D: 1. (CÈC)-D=Æ.

2. (CÈC)Ç`D)È ((XÈC)ÇD)=... =(`DÇC)È((C-D)Ç`C)=Æ.
3. `DÇC=Æ і (C-D)Ç`C=Æ.
4. Умова (C-D)ÌD чи CÌD; розв’язання (C-D)ÌCÌD.

2.2. Покриття і розбивки

Визначення. Покриттям непорожньої множини М називається множина Р його власних підмножин, об'єднання яких дорівнює М:

Р={M_і|1 £ і £½M½, Æ ¹ M_і, M_і Ì M, ÈM_і = M}

Визначення. Розбивкою непорожньої множини М називається множина R його власних попарно непересічних підмножин, об'єднання яких дорівнює М:

R={М_і|1 £ і £ ½M½, Æ ¹ M_і, M Ì M, M_і Ç M=Æ, ÈM_і = M}

Підмножини множини М, що входять у покриття Р (розбивка R), тобто М₁, М₂, М₃,..., М_|M|, називаються класами чи блоками покриття Р (розбивки R) і позначаються додатковими фігурними дужками: Р={{a, c}, {b, d, e}}, іноді – надкресленням без фігурних дужок.

Розбивка множини називається елементною, якщо кожен її клас - одноелементна множина, розбивка називається цілою, якщо складається з єдиного класу, що дорівнює вихідній множині. Елементна і ціла розбивки множин називаються тривіальними, інші, якщо існують, - нетривіальними.

Приклад.М={a, b, c, d, e, f}

P={{a, b, c,}, {b, d, e, f}, {e, f, a}}

R₁={{a, b}}, {c}, {d, e, f}}

R₂={{a}, {b}, {c}, {d}, {e}, {f}}

R₄={a, b, c, d, e, f}

2.3. Потужність множин. Зчисленні і континуальні множини

Множини бувають скінченними і нескінченними. Операції і властивості, що вивчені, справедливі для скінченних і нескінченних множин.

Порівняння множин зв'язане з установленням взаємооднозначної відповідності. Елементи множин М₁ і М₂ знаходяться у взаємооднозначній відповідності, якщо кожному елементу множини М₁ за деякім законом зіставлений єдиний елемент множини М₂ і навпаки. Такі множини називаються рівнопотужними (еквівалентними).

Приклад. Множина N рівно потужна множини N^2.

Множини, рівнопотужні множині натуральних чисел N, називаються зчисленними. Усяка нескінченна підмножина зчисленної множини також зчислена. Множини цілих, раціональних чисел, слів скінченної довжини в скінченному алфавіті зчисленні.

Теорема. Об'єднання скінченної чи зчисленної сукупності зчисленних множин також є зчисленною множиною.

Існують нескінченні множини, елементи яких не можна перерахувати.

Теорема Кантора. Множина усіх дійсних чисел інтервалу (0,1) числової осі незчисленна.

Усяка множина, еквівалентна множині всіх дійсних чисел інтервалу (0,1), називається континуальною (множиною потужності континууму).

Приклад. Множини ірраціональних, трансцендентних чисел незчисенні.

Теорема. Множина B(М) усіх підмножин деякої зчисленної множини М є множиною потужності континуума.

Нехай F(А) - множина усіх слів у скінченному алфавіті А. Будь-яка підмножина LÍF(A) називається мовою над алфавітом.

Приклад. Множина усіх мов над скінченним алфавітом є множиною потужності континуума.

Кардинальне число ãM множини М - це деЯкій об'єкт, що визначає потужність множини М (з розглянутої сукупності множин). У випадку скінченної множини М кардинальним числом ãМ=|M| кожної з множин розглянутої сукупності є натуральне число, що визначає число елементів у ньому і називане потужністю множини. Для нескінченних множин кардинальні числа називають трансфінітними.

Для кардинальних чисел скінченних множин можливі відношення:

1. ãM₁=ãM_2.

2. ãМ₁<ãM_2.

3. ãМ₁>ãM_2.

Приклад. M₁={1, 2, 3}, M₂={a, b, c}, M₁=M₂. M₃={1, 2, 3, 4}, M₄={a, b, c}, M₃>M₄.

При порівнянні нескінченних множин логічно можливі випадки:

1. Множини М₁ і М₂ рівно потужні, тобто ãМ₁=ãМ₂

2. Множини М₁ і М₂ не рівнопотужні, але одне з них, наприклад М₁, рівно потужне підмножині іншого - ãМ₁=ãМ₂^’ і М₂^’ÌM₂. У цьому випадку потужність множині М₁ менше потужності множині М₂, таким чином ãМ₁<ãM_2.

3. Множина М₁ еквівалентна (рівно потужна) деякій підмножині множині М₂ і, навпаки, множина М₂ еквівалентно (рівно потужна) деякій підмножині множині М₁. Випадок зводиться до першого.

Теорема Кантор-Бернштейна. Якщо множина М₁ еквівалентна (рівнопотужна) деякій підмножині множини М₂ і одночасно множина М₂ еквівалентна (рівнопотужна) деякій підмножині множини М₁, то множини М₁ і М₂ еквівалентні (рівнопотужні).

4. Множина М₁ не еквівалентна (нерівнопотужна) ніякій підмножині множини М₂ і множина М₂ не еквівалентна (нерівнопотужна) ніякій підмножині множини М₁, тобто М₁ і М₂ - непорівнянні. Цей випадок неможливий і множина усіх кардинальних чисел цілком упорядкована.

Приклад. M₁={mÎMmÎN & m – квадрат натурального числа}, M₂=N, c}, ãM₁=ãM₂, M₃=(0, ¥), M₄=(0, 1), ãM₃>ãM₄.

Наслідок. Якщо справедливе включення МÉM₁ÉM₂, причому М і М₂ – еквівалентні (рівно потужні), то М і М₁ еквівалентні (рівно потужні).

Приклад. M=(0, 1), M₁=(0, 1,5), M₂=(0, 2), ãM=ãM₂, М₂ÉM₁ÉM, ãM=ãM₂=ãM₁.

Наслідок. Якщо М₁ÊM₂, то ãМ₁³ãМ₂.

Наслідок. Якщо М - довільна кінцева множина, то М<ã₀, де ã₀- кардинальне число множини натуральних чисел N (будь-якої зчисленної множини), називане алеф-нуль.

Теорема. У всякій нескінченній множини М можна виділити деяку зчисленну підмножину.

Теорема. Потужність множини В(М) усіх підмножин будь-якої непорожньої множини М більше потужності даної множини, тобто ãВ(М)>ãМ.

Приклад. M₁={0, 1}, M₂=B(M)={{(0, 1}, {0}, {1}, Æ}, ãM₁<ãM₂.

Наслідок. Не існує множин найбільшої потужності, множина усіх кардинальних чисел не має максимального елемента.

Контрольні запитання

1. Що таке рівняння? Як виконується розв’язання рівнянь?

2. Яка різниця між покриттям і розбивкою?

3. Які блоки покрить і розбивок можуть бути?

4. У чому різниця скінченних і нескінченних множин?

5. Чи усі множини можна перерахувати?

6. Як порівнюються нескінченні множини?

7. Чи е найбільша множина, як це підтвердити?

Список літератури

Основна

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. - С.28-34. 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Вступ

Лекція має за мету висвітлити початкові поняття з теорії упорядкованих множин і графіків. Розглянути визначення упорядкованих множин і графіків, операції декартового (прямого) добутку, декартового ступеня, проекції, інверсії, композиції. Звернено повагу до властивостей функціональності та інверсії графіків, а також на властивості розглянутих операцій.

Лекція містить два підрозділи:

3.1. Упорядковані множини

3.2. Графіки

3.1. Упорядковані множини

Усяку множину можна упорядкувати, якщо кожному елементу ії поставити у відповідність деяке натуральне число від 1 до n, де
n - потужність множини. Таке число буде номером елемента.

Визначення. Упорядкованою множиною чи кортежем називається послідовність елементів множини, в якій кожен елемент займає визначене місце, елементи кортежу називаються його компонентами, число компонентів кортежу - n - його довжина

Приклад.А=<1, 2, 3>; B=<2, 1, 2>; C=(a, d, d)

Загальне позначення кортежу − пари кутових <...>, чи круглих (...) дужок, усередині яких задаються в упорядкованому вигляді компоненти кортежу. Конкретні кортежі, як і множини, позначаються великими латинськими літерами А₀, В₄, С_j, ..., компоненти кортежів позначаються рядковими латинськими літерами a, b₄, c_j, ... .

Кортежі вважаються рівними, якщо в них збігаються компоненти і порядок їхнього проходження − А=В, інакше кортежі не рівні − А¹В.

Компонентами кортежу можуть бути елементи множин, множини, інші кортежі. Ще одна назва кортежів - вектори чи n-ки (двійки, трійки,...).

Визначення. Прямим чи декартовим добутком множин А і В називається множина АхВ, що складається зі всіх упорядкованих пар, перший компонент яких належить множині А, а другий компонент належить множині В.

А×В={<a, b>ÎA×В|аÎА і bÎB}

Приклад. А={а, b}; B={1, 2}; A×В={<а, 1>, <а,2>, <b, 1>,<b,2>}.

Очевидно, що якщо ½A½=n, а ½B½=m, то ½AхВ½=n×m.

Визначення. Прямим декартовим добутком множин А₁, А₂, ..., А_n називається множина А₁×А₂×...×А_n, із усіх n-к, перший компонент яких належить множині А₁, другий компонент належить множині А₂, ..., n-а компонента належить множині А_n:

×А_і=А₁×А₂× ... ×А_n={<а₁, а₂, ..., а_n>ÎA₁×А₂×...×А_n| a₁ÎA₁, a₂ÎA₂, ..., a_nÎA_n}

Визначення. Прямий декартовий добуток множин А₁×А₂× ... ×А_n при рівних множинах А₁=А₂= ... =А_n=A називається прямим n-м декартовим ступенем множини А і позначається Аⁿ:

Аⁿ=A×А× ... ×А = {<a₁, a₂, ..., a_n>ÎAⁿ|a₁, a₂,..., a_nÎA}

При n=0 і n=1 по визначенню вважається А⁰={Æ} і А¹=А. Важливою підмножиною декартова добутку А×А є множина D_А={<а, а>|аÎА}, називана діагоналлю, що позначається також як E_A.

До кортежів чи множини кортежів однакової довжини застосовується унарна операція проекції.

Визначення. Проекцією кортежу А на і-ю вісь називається і-я компонента кортежу А, що позначається як пр_іА.

Проектування звичайне ведеться на сукупність упорядкованих по зростанню осей.

Приклад. А=<1, 2, 3, 3, 4>; пр₂А=2; пр₄А=3; пр_1,4А=<1, 3>.

Визначення. Проекцією множини М кортежів довжини n називається множина проекцій усіх кортежей з М

Приклад. М={<1, 2, 2, 3>, <а, b, c, d>, <a, 2, 4, c>}, пр₁М={1, а}; пр₁₃М={<1, 2>, <а, з>, <а, 4>}

Прямі декартові добуток і ступінь мають такими властивостями:

1. А×В¹В×А

2. А×(В×С)¹(А×В) ×С¹А×В×С

3. (АÈВ)×С=(А×С)È(В×С)

4. (АÇВ)×С=(А×С)Ç(В×С)

5. (АВ)×С=(А×С)(В×С)

6. А×А× ... ×А=Аⁿ.

7. А^l×А^м¹А^l+m.

8. А^l×А^м¹А^м×Аа^l.

9. А×Æ=Æ×А=Æ.

3.2. Графіки

Визначення. Множина Р називається графіком, якщо кожен його елемент є двійкою елементів деякої множини М.

Р={рÎR|р=< а, b> і а, bÎМ}

Приклад. Р={<а, b>, <1, c>, <2, 3>}

Якщо М - довільна множина, то М² - графік, будь-яка підмножина множини М² також є графіком.

Визначення. Множина проекцій графіка Р на першу вісь називається областю визначення графіка Р, множина проекцій графіка Р на другу вісь називається областю значень графіка.

Якщо відкласти по осі Х область визначення, а по осі Y область значень, то сам графік розміститься деякім чином на площині (рис. 3.1.).

Якщо графік Р=Æ, то очевидно ін₁Р=Æ і ін₂Р=Æ.

 

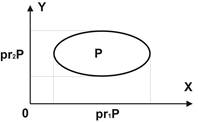
Рис. 3.1. Графік і його проекції на площині

 

Якщо графік по визначенню є множиною, то над графіками можуть виконуватися операції, що звичайна для множин, тобто È, Ç, , ù, -.

Визначення. Двійка < с, d> називається інверсією двійки <a, b>, якщо компоненти с дорівнює b, та d дорівнює a.

Інверсія пари р=<а, b> позначається як р^-1.

Подвійна інверсія двійки (р^-1)^-1 дорівнює самій двійці (р^-1)^-1=р.

Визначення. Інверсією графіка Р, що позначається як Р^-1, називається множина інверсій усіх пар з Р

Р^-1={qÎР^-1|q=p^-1 і рÎR}

Приклад. Р={<1, 2 >, < а, b>}, P^-1={<2, 1>, <b, a>}

При інверсії графіка Р пр₁R^-1=пр₂Р і пр₂R^-1=пр₁Р.

Визначення. Графік Р називається симетричним, якщо він поряд з кожною парою містить її інверсію

рÎR Þ р^-1ÎР

Приклад. р={<a, b>, <b, a>, <c, c>}

Для будь-якої множини М множина М² - симетричний графік, для будь-якого графіка Р РÈR^-1 і RÇR^-1 - симетричні графіки.

Визначення. Графік R=P°Q називається композицією графіків Р і Q, якщо двійка <х, у> належить R тоді і тільки тоді, коли існує такий елемент z, що двійка <х, z> належить Р и двійка <z, у> належить Q:

R=P°Q={<х, у>ÎR| існує z такий, що <х, z>ÎR і <z, у>Q}

Приклад. Р={<а, a>, <a, c>, <a, b>, <b, b>, <c, b>}

Q={<a, b>, <a, c>, <c, з>}

R=P_° Q={<a, b>, <a, c>}

Композиція графіків Р и Q порожня тоді, коли пр₂P₁Çпр₁P₂ = Æ.

Визначення. Декартовим добутком Р₁ і Р₂ називається графік

Р₁´Р₂={<<a₁, a₂>, <b₁, b₂>>|<а_і, b_і>ÎR_і , і=1,2}

Визначення. Графік Р називається функціональним, якщо в ньому немає пар з однаковими першими і різними другими компонентами; графік Р називається ін’єктивним, якщо в ньому немає пара з однаковими другими і різними першими компонентами.

Приклад. R₁={<a, b>, <a, з>} нефункціональний

R₂={<a, c>, <b, c>} неін’єктивний

Графік М² на довільній множині М не є функціональним і ін’єктивним, композиція функціональних графіків функціональна, композиція ін’єктивних графіків ін’єктивна, інверсія переводить функціональний графік у ін’єктивний, а ін’єктивний - у функціональний.

Операції над графіками мають спеціальні властивості:

1. Р₁°R₂¹R₂°R₁ не комутативність

2. R₁°(R₂°R₃)=(R₁°R₂)°R₃ асоціативність

3. R°Æ=Æ°R=Æ властивості границь

4. (Р₁°R₂)^-1=R₂^-1°R₁^-1

Контрольні запитання

1. Що таке упорядкована множина та як вона позначається?

2. Яка різниця між декартовим добутком і ступенем?

3. Які проекції можуть бути?

4. Які властивості мають операції над упорядкованими множинами?

5. Що є графіком?

6. Які операції можливі над графіками?

7. Які властивості мають графіки та операції над графіками?

Список літератури

Основна

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. - С.44-51. 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Вступ

Лекція має за мету висвітлити початкові поняття з відповідностей, образів і прообразів, відображень і діаграм. Розглянуті визначення відповідностей, образів і прообразів, відображень і діаграм, фактор-множини, характеристичні функції, операції об’єднання, Перетин, різниці, додатка, відмінні від простих множинних операцій, операції інверсії, декартового добутку, композиції, звуження, проеціювання. Звернено повагу до властивостей функціональності, ін'єктивності, скрізь визначеності, сюр'єктивності, бієктивності відповідностей, а також до властивостей розглянутих операцій, образів і комутативності діаграм.

Лекція містить три підрозділи:

4.1. Відповідності

4.2. Образи і прообрази

4.3. Відображення і діаграми

4.1. Відповідності

Нехай існують дві множини А і В, елементи яких можуть зіставлятися один одному і утворювати пари вигляду <a, b>. Якщо спосіб такого зіставлення визначений, тобто для (кожного) аÎA зазначений bÎB, з Якім а зіставляється, то між А і В установлена відповідність. При цьому не обов'язково, щоб у зіставленні брали участь всі елементи множин А і В.

Визначення. Відповідність - це трійка множин А, В, G, що позначається g=<A, B, G>, де третій компонент є підмножиною прямого добутку першого і другого компонентів, тобто GÍA´В. При цьому множина А називається областю відправлення відповідності, множина В - областю прибуття відповідності, множина G - графіком відповідності.

Приклад. g=<{a, b, c}, {1, 2, 3}, {<a, 1>, <a, 3>, <b, 2>}>

Визначення. Дві відповідності вважаються рівними тоді і тільки тоді, коли рівні їхні графіки, області відправлення і прибуття.

Відповідності не є множинами, у зв'язку з чим операції над ними відмінні від простих множинних операцій.

Визначення. Об'єднанням відповідностей g₁ і g₂, де g₁=<A₁, В₁, G₁>, g₂=<A₂, B₂, G₂>, називається відповідність

g₁Èg₂=<A₁ÈA₂, В₁ÈB₂, G₁ÈG₂>.

Визначення. Перетином відповідностей g₁ і g₂, де g=<A₁, B₁, G₁>, g₂=<A₂, B₂, G₂>, називається відповідність

g₁Çg₂=<A₁ÇA₂, B₁ÇB₂, G₁ÇG₂>.

Визначення. Різницею відповідностей g₁ і g₂, де g₁=(А₁, В₁, G₁), g₂=(A₂, B₂, G₂), називається відповідність

g₁g₂= (A₁ÇA₂, В₁ÇB₂, G₁G₂).

Визначення. Доповненням відповідності g=(А, В, G) називається відповідність

`g=(А, В, АхВG).

Приклад. g₁= ({a, b, c, d}, {1, 2, 3, 4}, {<a, 1>, <b, 2>, <c, 4>});

g₂=({b, c, d, e}, {2, 3, 4, 5, 6}, {<b, 2>, <b, 3>, <c, 4>, <e, 6>};

g₁Èg₂=({a, b, c, d, e}, {1, 2, 3, 4, 5, 6}, {<a, 1>, <b, 2>, <b, 3>, <c, 4>, <e, 6>});

g₁Çg₂=({b, c, d}, {2, 3, 4}, {<b, 2>, <c, 4>});

g₁g₂=({b, c, d}, {2, 3, 4}, {<a, 1>});

g₂g₁=({b, c, d}, {2, 3, 4}, {<b, 3>, <e, 6>});

g₁-g₂=({b, c, d}, {2, 3, 4}, {<a, 1>, <b, 3>, <e, 6>});

`g₁=({a, b, c, d}, {1, 2, 3, 4}, {<a, 2>, <a, 3>, <a, 4>, <b, 1>, <b, 3>, <b, 4>, <c, 1>, <c, 2>, <c, 3>, <d, 1>, <d, 2>, <d, 3>, <d, 4>})

Визначення. Інверсією відповідності g=(А, В, G) чи оберненою відповідністю, що позначається як g^--1, називається відповідність, у якій, по-перше, область відправлення дорівнює області прибуття вихідної відповідності g, по-друге, область прибуття дорівнює області відправлення вихідної відповідності g, по-третє, графік дорівнює інверсії графіка G вихідної відповідності g, тобто
g^--1=(В, А, G^-1).

Очевидно, що інверсія відповідності g^-1 дорівнює самій
відповідності g, тобто(g^-1)^-1=g.

З рівності відповідності своєї інверсії, тобто з g=g^-1, випливає, що графік G - симетричний, а множини А і В рівні: А=В.

З g=(А, В, Æ) випливає g^-1=(В, А, Æ).

Визначення. Декартовим добутком відповідностей g₁ і g₂ називається відповідність

g₁´g₂=(А₁´А₂, В₁´В₂, G₁´G₂)

Приклад.

g₁´g₂=({<a, b>, <a, c>, <a, d>, <a, e>, <b, b>, <b, c>,...,<d, b>, <d, c>, <d, d>, <d, e>}, {<1, 2>, <1, 3>, <1, 4>, <1, 5>, <1, 6>, <2, 2>, <2, 3>,...,<4, 2>, <4, 3>, <4, 4>, <4, 5>, <4, 6>}, {<<a, b>, <1, 2>>, <<a, b>, <1, 3>>, <<a, c>, <1, 4>>, <a, e>, <1, 6>>,...,<<c, c>, <4, 4>>, <<c, e>, <4, 6>>})

Визначення. Композицією відповідностей g₁ і g₂, що позначається g₁°g₂, називається відповідність, у якій область відправлення дорівнює області відправлення відповідності g₁, область прибуття дорівнює області прибуття відповідності g₂, графік відповідності дорівнює композиції графіків відповідностей g₁ і g₂, тобто
g₁°g₂=(А₁, В₂, G₁° G₂).

Приклад. g₁=({a,b,c,d,},{0,1,2,3,4,},{(a,1),(b,0),(c,1),(d,2),(d,3)}), g₁=({1,2,3,4,5},{I,II,III},{(1,I).(1,II),(2,II),(3,III),(4,III), (5,III)}), g₂°g₂=({a,b,c,d},{I,II,III},{(a,I),(a,II),(c,I),(c,II),(d,II),(d,III)})

Визначення. Звуженням чи обмеженням відповідності g=(А, В, G) на множину А¢ÍA, що позначається g_A’, називається відповідність
g_A’ = (А¢, В, GÇ(А¢хВ)).

Приклад.g=({a,b,c},{1,2,3}{(a,1),(a,2),(c,3)}), А¢={a, b},
g_A’=({a,b},{1,2,3},{(a,1),(a,2)}).

У цьому випадку відповідність g називається розширенням чи продовженням відповідності g_A’.

Включення g₁Íg₂ виконується по визначенню тоді і тільки тоді, коли А₁ÍА₂, В₁ÍB₂, G₁ÍG₂.

Визначення. Відповідність g=(А, В, G) називається:

а) функціональною чи функцією, якщо її графік G функціональний;

б) ін’єктивною чи ін'єкцією, якщо її графік G ін'єктивний;

в) скрізь визначеною, якщо її область визначення збігається з областю відправлення, тобто пр₁G=А;

г) сюр'єктивною чи сюр'єкцією, якщо її область значень збігається з областю прибуття, тобто пр₂G=В;

д) бієктивною чи бієкцією, якщо вона функціональна, ін'єктивна, скрізь визначена і сюр'єктивна (інша назва бієкції - однозначна відповідність).

Справедливі таки твердження і властивості:

1. g₁° g₂ ¹ g₂° g₁ некомутативність

2. g₁°(g₂° g₃)=(g₁° g₂) ° g₃ асоціативність

3. (g₁° g₂)^-1=g₂^-1 ° g₁^-1

4. g - функція Û g^--1 ін'єкція

5. g - сюр'єкція Û g^--1 скрізь визначена

6. g - бієкція Û g^-1 бієкція

4.2. Образи і прообрази

Визначення. Образом множини А¢ при відповідності g, що позначається g(А¢), називається множина усіх тих і тільки тих других компонентів двійок графіка G, для яких перші компоненти належать множині А¢:

g(А¢)= {bÎg(A¢ )|<a, b>ÎG і аÎA¢}.

Приклад. g₃=({a,b,c},{1,2,3,4}{(a,1),(a,3),(b,1),(b,4),(c,2)}),
А¢={a, c, d} і A¢ÇA¹Æ, g₃(A¢ )={1, 2, 3}

Образ множини g(А¢ ) також називається перерізом відповідності g по множині А¢.

Визначення. Множина перерізів відповідності g по кожному з елементів області відправлення називається фактором-множиною відповідності g і позначається g_F .

Приклад. g_1F={{1}, {2}, {4}, Æ} для g₁

g_3F={{1, 3}, {1, 2, 4}, {2}} для g₃.

Визначення. Повним прообразом чи прообразом множини В¢ при відповідності g, що позначається g^--1(В¢), називається множина усіх тих і тільки тих перших компонентів пари графіка G, для яких другі компоненти належать множини В¢:

g^--1(В¢ )={aÎg^--1(B¢ )|<a, b>ÎG і bÎB¢}.

Приклад. g=({a,b,c},{1,2,3}{(a,1),(b,2),(b,3),(c,2)}), B¢={1, 3, 4} і В¢ÇB¹Æ, g^-1(В¢ )={a, b}.

Образи і прообрази мають властивості:

1. g(А)Íпр₂G g^--1(B)Íпр₁G

2. A¢ÍA²Þg(A¢)Íg(A²) B¢ÍB²Þg^--1(B¢)Íg^-1(B²)

3. g(A¢)=g(A¢Çпр₁G) g^--1(B¢)=g^--1(B¢Çпр₂G)

4. g(A¢)=ÆÛA¢Çпр₁G=Æ g^--1(B¢)=ÆÛB¢Çпр₂G=Æ

5. g(пр₁G)=пр₂G g^--1(пр₂G)=пр₁G

6. g(Æ)=Æ g^--1(Æ)=Æ

4.3. Відображення і діаграми

Визначення. Відповідність g=(А, В, G) називається відображенням з множини А в множину В, чи просто відображенням, якщо воно скрізь визначене і функціональне, частковим відображенням з множини А в множину В, якщо воно функціональне.

Відображення g скінченної множини М={m₁, m₂, ..., m_n} у себе часто являють 2´n-матрицею:

m₁, m₂, ... m_n

g(m₁) g(m₂) … g(m_n)

Композиція відображень такого вигляду може бути визначена по цих матрицях. Якщо множина М - звичайна, то ін'єкція (сюр'єкція) М в себе є також бієкцією і називається підстановкою множини М.

Нехай g - відповідність, на основі визначення множини g(A¢) для A¢ÍA відповідності g може бути зіставлене відображення з Р(А) у Р(В). Аналогічно, відображення з Р(В) у Р(А) може бути зіставлено відповідності g^-1.

Нехай g=(А, В, G) - відображення, і А¢, А²ÍА и В¢, В²ÍB. Тоді виконуються відношення:

1. g(A¢ÈA²)=g(A¢)Èg(A²)

2. g(A¢ÇA²)Íg(A¢)Çg(A²) (рівність - при ін'єкції для звуження A¢ÇA²)

3. g^--1(B¢ÈB²)=g^--1(B¢)Èg^--1(B²)

4. g^--1(B¢ÇB²)=g^--1(B¢)Çg^--1(B²)

Крім того, для ін¢єктивності і сюр¢єктивності еквівалентні три наступні вираження:

1. g: A®B ін’єктивно (сюр’єктивно);

2. g: Р(А)®Р(В) сюр’єктивно (ін’єктивно);

3. g^--1: Р(В)®Р(А) сюр’єктивно (ін’єктивно).

Визначення. Якщо М¢ є підмножиною множини М, тобто М¢ÍМ, то характеристичною функцією М¢ у М називається відображення G_M¢^M:

G_M¢^M: М®{0, 1} = G_M¢^M(m)=1, якщо mÎM¢

G_M¢^M(m)=0 у противному випадку

Визначення. Нехай М=М₁´ ... ´M_n - декартів добуток, тоді для кожної з множини {1, ... , n}, як відзначалося раніше, визначені відображення рr_і,`рr_і, називані проекціями:

рr_і: М®M_і, рr_і(m₁, ... , m_і, ... , m_n)=m_і;

ù рr_і: М®M₁´ ... ´M_і-1´M_і+1´ ... ´M_n;

ù рr_і(m₁, ... , m_і-1, m_і, m_і+1, ... , m_n)=(m₁, m₂, ... , m_і-1, m_і+1, ... , m_n).

Якщо 1£ k £n і 1£ і₁<і₂<....<і_k£n, проекція рr_і1, _і2, ..., _ік М®M_і1´M_і2´...´M_іk визначена рівністю рr_{і1, і2, ..., ік}(m₁, m₂, ..., m_n)=(m_і1, m_і2, ..., m_ік).

Для полегшення роботи з відображеннями застосовуються діаграми. Нехай дані відображення g_і=(Аі, Аі₊₂ Gі) при і=1, 2 і g¢_j=(A_j, A_{j+1, G}¢_j) при j=1, 3, їм відповідає прямокутна діаграма (рис. 4.1).

Ця діаграма називається комутативною тоді і тільки тоді, коли g₁°g¢₃(а)=g₁¢°g₃(а) для всіх аÎA₁. Аналогічно можна представити комутативність трикутних, прямих та інших діаграм.

 

Рис. 4.1. Прямокутна діаграма для відображень: gі=(Аі, Аі+2 Gі) при і=1, 2 і g¢j=(Aj, Aj+1, G¢j) при j=1, 3

Контрольні запитання

1. Яка різниця між графіком і відповідністю?

2. Які особливості мають операції для відповідностей?

3. Які властивості мають відповідності та їх операції?

4. Що є образом і повним прообразом?

5. Які властивості мають образи і прообрази?

6. Що є відображенням та які властивості вони мають?

7. Що є характеристичною функцією і діаграмою?

Список літератури

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.33-41. 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Вступ

Лекція має за мету висвітлити початкові поняття з відношень і графіків відношень. Розглянуті визначення і n-арність відношень, типові відношення, множинні операції об’єднання, перетин, різниці, симетричної різниці, декартова добутку. Звернено повагу на ототожнення відношень і їх графіків, що часто використаємо, а також асоціативність декартова добутку відношень.

Лекція містить два підрозділи:

5.1. Основні поняття відношень

5.2. Множинні операції відношень

5.1. Основні поняття відношень

Визначення. Під n-арним відношенням чи n-відношенням rⁿ на множинах А₁, А₂, ..., А_n розуміється закон (характеристична властивість), що виділяє в декартовому добутку А₁´A₂´...´A_n деяку підмножину rⁿ_A1,...,AnÍA₁´A₂´...´A_n, що називана (n-вимірним) графіком відношення rⁿ. Якщо А₁=А₂=...=А_n=A, то говорять про n-відношення rⁿ на множині А з графіком rⁿ_AÍAⁿ.

Відношення, як і відповідності, часто позначають грецькими літерами, з індексами чи без них, і спеціальними символами =, £, ³, <, >.

Часто поняття n-відношення ототожнюється з його графіком, тобто під n-відношенням rⁿ на множинах А₁, А₂, ..., А_n розуміється сама підмножина:

rⁿ_A1,¼,AnÍA₁´A₂´¼´A_n.

Якщо a=(а₁, а₂,..., а_n)Îrⁿ_{1,.., An}, де а_jÎA_j, j=1, 2,..., n, то говорять, що елементи а₁, а₂,..., а_n знаходяться у відношенні rⁿ: rⁿ(a₁, a₂, ..., a_n), так що позначення (а₁, a₂, ..., a_n)Î rⁿ і rⁿ(a₁, a₂, ... , a_n) рівносильні.

Визначення. Послідовність a=(а₁, a₂, ... , a_n)Îrⁿ_A1,...,An називається елементом чи вектором n-відношення rⁿ. Відношення, графіки яких містять скінченні множини векторів, називають скінченними
n-відношеннями. Якщо rⁿ_1,...,An=Æ, то rⁿ- порожнє n-відношення (Ùⁿ), якщо rⁿ_{1, ..., An}=A₁´A₂´¼´A_n, то rⁿ- універсальне n-відношення (Úⁿ).

Тому що n-відношення rⁿ можна розглядати як підмножини декартова добутку А₁´A₂´¼´А_n, існують різні способи завдання
n-відношень, аналогічні способам завдання множин. Так графік rⁿ_{1, ...,An} зручно задавати матрицею, рядками якої є вектори відношення rⁿ.

Приклад. rⁿ_{1, ..., An}={a ^j=(a₁ ^j, a₂ ^j, ... , a_n ^j|j=1, 2, ... , r} - множина усіх векторів, графік у матричній формі

rⁿ_{A1, ..., An}= a₁ ^j1 a₂ ^j1 ... a_n ^j1

a₁ ^ji2 a₂ ^j2 ... a_n ^j2

..................................

a₁ ^jr a₂ ^jr ... a_n ^jr

Відношення r¹ на множини А називають унарними, відношення r² на А, В - бінарними, відношення r³ на А, В, С - тернарними і т.д.

Унарне відношення r¹ на множини А є характеристичною властивістю деякої підмножини r¹_АÎA - графіка даного відношення, таким чином, множина всіх унарних відношень на А збігається з множиною всіх підмножин множини А. Якщо ½А½=n, то число унарних відношень на А дорівнює 2ⁿ.

Лема. Будь-якому n-відношенню r ⁿ на множинах А₁, А₂, ..., А_n відповідає унарне відношення r¹ на множини А₁´A₂´¼´A_n таке, що виконується r¹(a) тоді і тільки тоді, коли для відношення виконується r ⁿ(a₁ ^і, a₂ ^і..., a_n ^і), де a=(a₁ ^і, a₂ ^і, ..., a_n ^і) - довільний вектор відношення r ⁿ.

Бінарне відношення r на множинах А і В визначається графіком r_A,BÍA´B. Якщо елементи аÎA і bÎB знаходяться у відношенні r, то поряд з позначеннями (а, b)Îr_A,B і r(a, b) використовується й аrb.

Приклад. а)А={2, 3, 5} r_A,B= 2 2

B={2, 3, 4, 5, 6} 2 4

3 3

3 6

5 5

б) Таблиця 5.1

rA,B
	х		х		х
		х			х
				х

 

в)

Рис. 5.1. Бінарне відношення r_A,B

Графік тернарного відношення r³ має вигляд r³_A,B,CÍA´B´С.

З кожною бінарною операцією F(х,у), зокрема з арифметичними операціями “+” , ”-”, ”×”, ”:” і іншими, може бути зв'язане тернарне відношення j³ таке, що j³(х, у, z) тоді і тільки тоді, коли F(х, у)=z.

Найбільше часто вживаються бінарні відношення (графіки на площині).

Якщо для бінарного відношення r²_А1,А2ÍА₁´A₂ множини А₁ і А₂ рівні А, то говорять, що визначено відношення на множині А, тобто r²_А.

Визначення. Відношення на множині А називається

а) повним, якщо r²_А=А²;

б) порожнім і позначається 0_А, якщо r²_А=Æ;

в) відношенням рівності і позначається Е_А, якщо і тільки якщо r²_А містить всі можливі пари з однаковими компонентами;

г) відношенням нерівності, якщо r²_А не містить ні однієї пари з однаковими компонентами.

5.2. Множинні операції відношень

Вивчення n-відношень на множинах А₁, А₂, ..., А_n можна зв'язати з вивченням їхніх графіків, тобто підмножин А₁´A₂´¼´A_n. На множини
n-відношень поширюються множинні операції “È”, ”Ç”, ””, ”-”, ”ù” і множинні відношення включення “Í”, тобто з rⁿ _{A1, A2, ..., An} Ísⁿ _{A1, A2, ..., An}- включення графіків випливає включення відношень rⁿÍsⁿ.

Визначення. Об'єднання відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ È s ⁿ з графіком q ⁿ _{A1, A2, ..., An}=r ⁿ _{A1, A2, ..., An} È s ⁿ _{A1, A2, ..., An}.

Визначення. Перетин відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ Ç s ⁿ з графіком q ⁿ _{A1, A2, ..., An}=r ⁿ _{A1, A2, ..., An} Ç s ⁿ _{A1, A2, ..., An}.

Визначення. Різниця відношень r ⁿ і s ⁿ - то відношення
q ⁿ=r ⁿ s ⁿ з графіком q ⁿ _{A1, A2, ..., An}=r ⁿ _{A1, A2, ..., An} s ⁿ _{A1, A2, ..., An.}

Визначення. Симетрична різниця відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ - s ⁿ з графіком q ⁿ _{A1, A2, ..., An}=r ⁿ _{A1, A2, ..., An} - s ⁿ _{A1, A2 ..., An}.

Визначення. Відношення`r <sup>n</sup> називається доповненням відношення r<sup>n</sup>, якщо a Î r <sup>n</sup> <sub>A1, A2, ..., An</sub> тоді і тільки тоді, коли`a Ï r ⁿ _{A1, A2, ..., An}

Приклад. Для бінарних відношень <, =, £, ³, > справедливо

£_N = <_N È =_N; =_N = £_N Ç ³_N; <_N =`³_N.

Нехай rⁿ - відношення на множинах А₁, А₂, ..., А_n, а s^m - відношення на множинах Аn₊₁, ..., A_n+m.

Визначення. Декартів добуток відношень r ⁿ і s ^m - це відношення
q ^n+m=r ⁿ´s ^m, графік якого має вигляд

q ^n+m _{A1, A2, ..., An+m}=r ⁿ _{A1, A2, ..., An} ´ s ^m_{An+1, ..., An+m}.

Слід мати на увазі, що в цьому випадку допускається асоціативність декартова добутку.

Приклад. Нехай А₁={0, 1, 2}, A₂={a, b}, A₃={b, c, d} і a ³, b ³ – відношення:

a ²_{A1, A2}= 0 a b ³_{A1, A2, A3}= 0 a b

1 b 1 b c

1 b d

Тоді відношення g ⁵=a ²´b ³ визначається графіком:

g⁵_{A1, A2, A3 A4, A5}= 0 a ´ 0 a b = 0 a 0 a b

1 b 1 b c 0 a 1 d c

1 b d 0 a 1 b d

1 b 0 a b

1 b 1 b c

1 b 1 b d

Контрольні запитання

1. Що є n-арне відношення?

2. Як можна зіставити n-арному відношенню унарне відношення?

3. Як можна зіставити бінарної операції тернарне відношення?

4. Які способи завдання відношень існують?

5. Які типові відношення існують?

6. Які множинні операції для відношень?

7. Що є асоціативністю декартова добутку відношень?

Список літератури

Основна

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. с.35-46. 3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. –… 4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.97-115.

Вступ

Лекція має за мету висвітлити поняття спеціальних операцій для n-арних відношень. Розглянуті операції перестановки і ототожнення координат, приписування фіктивної координати, згортки де Моргана і суперпозиції. Звернено повагу на спеціальні часткові випадки перестановки – цикл, транспозицію, зворотну перестановку, поняття діагоналі, властивості згортки де Моргана, узагальнення між операціями композиції, згортки де Моргана і суперпозиції, що часто використовуються.

У лекції присутні два підрозділи:

6.1. Перестановка, ототожнення, приписування фіктивної координати

6.2. Згортка де Моргана, суперпозиція

6.1. Перестановка, ототожнення, приписування фіктивної координати

Крім множинних операцій, у теорії n-відношень використовуються спеціальні операції перестановки й ототожнення координат (стовпців), приписування фіктивної координати, а також згортки де-Моргана. Нехай rⁿ – відношення на множинах А₁, А₂, … , А_n, k=(1, 2, …, n) – набір координат (номерів) стовпців у матриці графіка rⁿ_{1, … , An}, k¢=(і₁, і₂, … , i_n) – набір, отриманий з k у результаті деякої перестановки елементів.

Визначення. Операція h_к’(rⁿ) перестановки координат породжує ставлення n-відношення gⁿ на множинах Аi₁, A_i2, …, A_in, графік якого gⁿ_{Ai, … , Ain} виходить із графіка rⁿ_1,…,An, перестановкою його стовпців відповідно до набору k¢.

Визначення. Нехай k₀=(2, 3, …, n, 1). Перестановка h_k0(rⁿ) називається циклом і позначається x(rⁿ).

Визначення. Нехай k₁=(2, 1, 3, … , n). Перестановка h_k1(rⁿ) називається транспозицією і позначається t(rⁿ).

За допомогою циклу n транспозиції можна виразити будь-яку перестановку h(rⁿ).

Нехай`k=(n, n-1, …, 2, 1).

Визначення. Відношення (rⁿ)^-1=h<sub>`k</sub>(r<sub>n</sub>) над множинами A<sub>n</sub>, A<sub>n-1</sub>,…, A<sub>2</sub>, A<sub>1</sub>, отримане з відношення r<sup>n</sup> у результаті перестановки, що відповідає набору`k називається оберненим.

Очевидно, a=(a_n, a_n-1, …, a₂, a₁)Î(rⁿ)^-1_{An, …, A1}, тоді і тільки тоді, коли
a^-1=(a₁, a_2,,…, a_n)Îrⁿ_{1, An}

Приклад. Для бінарних відношень <, >, £, ³ справедливо
<^---1=>, >^--1=<, £^--1=³,³^--1=£ (Операція перестановки).

Операція перестановки для бінарних відношень є інверсією.

Для обернання n-відношень виконуються рівності (при rⁿÍsⁿ):

1. ((rⁿ)^-1)^-1=rⁿ

2. (rⁿ)^-1Í(sⁿ)^-1

3. (Çr_iⁿ)^-1=Ç(r_iⁿ)^-1

4. (Èr_iⁿ)^-1=È(r_iⁿ)^-1

5. (`rⁿ)^-1=ù((rⁿ)^-1)

З рівностей випливає, що для Ф^-1(r₁ⁿ, r₂ⁿ,..., r_kⁿ)=F((r₁ⁿ)^-1, (r₂ⁿ)^-1,..., (r_kⁿ)^-1),
де Ф – формула, побудована з відношень r₁ⁿ, ..., r_kⁿ за допомогою операцій È, Ç, ù. Крім того, справедлива рівність

6. (rⁿ´s^m)^-1 = (s^m)^-1´(rⁿ)^-1.

Нехай rⁿ – відношення на множинах А₁, …, А_n і {j₁, j₂, …, j_l} - деяка підмножина множини номерів {1, 2, …, n}.

Визначення. Операція ототожнення координат d(rⁿ) породжує відношення q ^n-l+l= d_{j1,j2 . , jl}(rⁿ) на множинах A₁,…, A_j2-1, A_j2+1, …, A_j3-1, A_j3+1, …, A_jl-1, A_jl+1, …, A_n, графік якого виходить із графіка rⁿ_1,…An
у результаті виділення множини векторів {a=(а₁^і, a₂ⁱ, …, a_nⁱ)| a_j1ⁱ=a_j2ⁱ=…=a_jl ⁱ}Írⁿ_{1,…, An} з наступним викреслюванням у кожнім векторі a елементів a_j2ⁱ, a_j3ⁱ, …, a_jl ⁱ.

Тобто у відношенні rⁿ виділяються усі вектори, в яких збігаються компоненти, розташовані в стовпцях з координатами j₁, …, j_i, з наступним виключенням стовпців-копій, що мають координати j₂, j₃, …, j_i.

Приклад. Для відношення g⁵_{А1,А2,А3,А4,А5} з попереднього приклада d₂₄(g⁵)=q ⁴, де q ⁴:

q ⁴_{А1,А2,А1,А3}= 0, a, 0, b

1, b, 1, c

1, b, 1, d

Для відношення q ⁴ d₁₃(q ⁴⁾=x³, де x³:

x³_А1,А2,А3 = 0, a, b

1, b, c

1, b, d

Якщо l=2, j₁=1, j₂=2, то ототожнення d₁₂(rⁿ) позначається d(rⁿ). За допомогою d(rⁿ) і перестановки координат можна зробити будь-яке ототожнення координат.

Визначення. Відношення dⁿ на множині А називається діагоналлю, якщо для будь-якого аÎA виконується (a, …, a)Îdⁿ.

Приклад. Бінарне відношення рівності на множині N - діагональ. Якщо d_1,2,…n(rⁿ)- відношення на множини А, то d_1,2,…n(rⁿ)Ídⁿ. Крім того, для будь-якого відношення rⁿÍdⁿ виконується (rⁿ)^—1=rⁿ.

Визначення. Операція приписування фіктивної координати "(rⁿ) породжує відношення qⁿ⁺¹="(rⁿ) над множинами A, A₁, A₂, ..., A_n таке, що при справедливості rⁿ(а₁ ^j, a₂ ^j, ..., a_n ^j) виконується
q ⁿ⁺¹(a, a₁ ^j, a₂ ^j, ..., a_n ^j) для будь-якого аÎA.

Операція приписування відношенню rⁿ фіктивної координати по множині А полягає в утворенні відношення qⁿ⁺¹="(rⁿ) із графіком, одержуваним таким чином: для кожного вектора a=(a₁ⁱ, a₂ⁱ, …, a_nⁱ)Îrⁿ_1,…,An будуються вектори (а, а₁^і, a₂ⁱ, …, a_nⁱ)Î qⁿ⁺¹_A,A1,…,An, отримані приписуванням до вектора a ліворуч по черзі всіх елементів множини А.

Приклад. Для a³ на множини А={0,1} із графіком

a³_А= 1, 0, 0

0, 1, 0

0, 0, 1

у результаті приписування фіктивної (на множині А) координати

a⁴_А= 0, 1, 0, 0

0, 0, 1, 0

0, 0, 0, 1

1, 1, 0, 0

1, 0, 1, 0

1, 0, 0, 1

Операція ", зокрема, вирівнює арності у відношеннях.

6.2. Згортка де Моргана, суперпозиція

Одна з важливих операцій над відношеннями – згортка де Моргана.

Нехай rⁿ – відношення на множинах А₁, А₂, … , Аn_{-1, A, a} s^m відношення на множинах A, A_n, A_n+1, … , A_n+m-2.

Визначення. Операція згортки де Моргана для відношень rⁿ і s^m породжує відношення q^n+m-2=rⁿ*s^m над множинами А₁, А₂, …, Аn_+m-2, таке, що q^n+m-2(a₁^і, a₂^і,…, a_in+m-2^j) виконується тоді і тільки тоді, коли знайдеться аÎA, для якого виконується rⁿ(a₁^і, a₂^і, …, a_n-1^і, a) і s^m(a, a_n^і, a_n+1^і, …, a_n+m-2^і).

Приклад. aⁿ_1,…,An= 1, 2, … n

2, 3, … n+1

…............................................................

k-2n+2 k-2n+3 … k-n+1

 

gⁿ_{An, …, A1}= n, n-1, … 1

n+1, n, … 2

….............................................................

k-n+1, k-n, … k-2n+2

q ^2n-2_{A1,…,An-1,An+1,…A1}=1, 2, … n-1, n-1 … 2, 1

2, 3, … n, n … 3 2

…........................................................................

k-2n+2, k-2n+3, … k-n, k-n, … k-2n+3, k-2n+2

Приклад. Графік згортки a*b бінарних відношень a і b на множинах А={a, b, c} і B={0, 1, 2}=C із графіками

a_АВ= а, 0 b_BC= 0, 1

b, 1 0, 2

c, 2 1, 2

2, 2

має вигляд (a*b)= a, 1

a, 2

b, 2

c, 2

Операція згортки не комутативна, але асоціативна.

1. rⁿ*s^m¹ s^m*rⁿ

2. (rⁿ*s^m)*q ^k= rⁿ*(s^m*q ^k)

Справедлива рівність

3. (rⁿ*s^m)^-1=(s^m)^-1*(rⁿ)^-1

Нехай r - бінарне відношення на множинах А, В, s - бінарне відношення на множинах В, С. Згортка бінарних відношень r і s називається їхньою композицією.

Операція композиції бінарних відношень допускає й інші узагальнення на n-арний випадок.

Приклад. Нехай L₁, L₂, L₃ – алгоритмічні мови, а p і p’ - відношення перекладу відповідно з L₁ на L₂ і з L₂ на L₃. Тоді композиція p²=p*p¢ відношень p і p’ також є відношенням перекладу з мови L₁ на L₃.

Нехай r₁^m – відношення на множинах А₁,…,А_m-1, B₁; r₂^m на множинах А₁,…,А_m-1, B₂;…;r_n-1^m – на множинах А₁,…,А_m-1, B_n-1; sⁿ – на множинах У₁,…,Вn_-1, A_m.

Визначення. Суперпозицією відношень r₁^m,r₂^m,…,r_n-1^m,sⁿ називається m-відношення q^m=sⁿ(r₁^m,r₂^m,…,r_n-1^m) на множинах А₁,A₂,…,А_m таке, що q^m(а₁^і, a₂^і,…,a_mⁱ) тоді і тільки тоді, коли знайдуться елементи b₁^jÎB₁, b₂^j ÎB₂,…,b_n-1^jÎB_n-1, для яких r_s^m(а₁^і, a₂^і,…,a_m-1ⁱ,b_s^j при будь-якому s=1, 2,…,n-1, причому, sⁿ(b₁^j, b₂^j, b_n-1^j, a_m^і).

Приклад. r₁³ = 0, 1, 1 r₂³ = 0, 0, 0 r₃³ = 0, 0, 1 s ⁴= 0, 0, 0, 0

1, 0, 0 0, 1, 0 0, 1, 1 1, 0, 1, 1

1, 1, 1 1, 1, 1 1, 1, 0 1, 1, 0, 0

1, 1, 1 1, 1, 1, 1

q ³=s⁴(r₁³,r₂³,r₃³)= 0, 1, 1

1, 1, 0

1, 1, 1

Окремним випадком суперпозиції для двох відношень є згортка де-Моргана.

Контрольні запитання

2. Які властивості мають обернення n-арного відношення? 3. Як виконується ототожнення координат n-арного відношення? 4. Що є діагоналлю відношення і для яких відношень діагональ має існувати?

Основна

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.43-46. 3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. –… 4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.97-115.

Вступ

Лекція має за мету висвітлити поняття основних властивостей для n-арних відношень. Розглянуто властивості, що є успадкованими від відповідностей, а також власні властивості відношень. Звернено повагу на особливості успадкування, а також на чотири групи властивостей n-арних відношень – рефлексивність, симетричність, транзитивність, зв’язність, деякі з котрих визначені через бінарні відношення.

У лекції присутні два підрозділи:

7.1. Успадковані властивості відношень

7.2. Спеціальні властивості відношень

7.1. Успадковані властивості відношень

Нехай rⁿ - відношення на множинах А₁, А₂, ..., А_n із графіком

rⁿ_{A1, ..., An}= a₁ⁱ¹, a₂ⁱ¹, ... a_nⁱ¹

a₁ⁱ² a₂ⁱ², ... a_nⁱ²

.................................

a₁^ir a₂^ir, ... a_n^ir

Визначення. Проекцією відношення rⁿ на множину А_j (при будь-якому j=1, 2, ..., n), називається множина рr_j(rⁿ)={a_jⁱ¹, a_jⁱ², a_j^ir}ÍA_j всіх елементів j-го стовпця матриці rⁿ_{1, An}, тобто проекція відношення rⁿ на множину А_j – це сукупність j-х компонент усіх векторів відношення rⁿ.

Визначення. Перерізом (січенням) S^(j)a₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ відношення rⁿ по елементах a₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ називається множина всіх елементів a_j^irÎA_j, для яких виконується rⁿ(a₁^і…,a_j-1ⁱ,a_jⁱ,a_j+1ⁱ,…,a_nⁱ), тобто S^(j)a₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ(rⁿ)={a_j^ir| rⁿ(a₁ⁱ,…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ)}, де j=1, 2,…,n.

Нехай A_j/rⁿ={S^(j)а₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ(rⁿ)}–множина Перерізів відношення rⁿ по всяких сукупностях (а₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ)Î
ÎА₁´А₂´…´А_j-1´A_j+1´…´A_n. Множина A_j/rⁿ називається фактор-множиною A_j по відношенню rⁿ. Замість однієї послідовності (а₁^і…,a_j-1ⁱ,a_j+1ⁱ,…,a_nⁱ) можна розглядати їхню сукупність Х={(а₁^ir…,a_j-1^ir,a_j+1^ir,…,a_n^ir)½r=1,2,…,k}... Переріз S^(j)_X(rⁿ) відношення по сукупності Х є об'єднанням перерізів відношення rⁿ по всіх послідовностях, що входять у Х: S^(j)_X(rⁿ)=È_r=1^k (S^(j)а₁^ir…,a_j-1^ir,a_j+1^ir,…,a_n^ir(rⁿ)).

Приклад. Нехай відношення a³ на множинах А={a₁, a₂}, BB={b₁, b₂, b₃} і C={0,1}, що е a³ Í А´B´C, визначено з допомогою матриці

a³= a1, b1, 0

a1, b2, 0

a2, b1, 1

a2, b2, 1

a2, b2, 0,

тоді pr₁(a³⁾=A, pr₂(a³⁾={b₁, b₂}, pr₃(a³⁾=C,

S⁽¹⁾_b2,0(a³⁾={a₁,a₂}, S⁽²⁾_a1,0(a³⁾={b₁,b₂},

C/a³={S⁽³⁾a₁,b₁, S⁽³⁾a₂,b₁, S⁽³⁾a₁,b₂, S⁽³⁾a₂,b₂, S⁽³⁾a₁,b₃, S⁽³⁾a₂,b₃},

для множини X={(a₁, b₁),(a₂, b₁)} S⁽³⁾_X(a³⁾=S⁽³⁾a₁,b₁È S⁽³⁾a₂,b₁=C.

Визначення. Відношення jⁿ на множинах А₁, А₂,…,А_n називається функціональним при відображенні його в бінарне відношення j² на множинах (А₁´ А₂´…´А_n) і А_n, якщо для кожної послідовності елементів (а₁^і…,a₂ⁱ,…,a_n-1ⁱ)ÎА₁´А₂´…´А_n-1 переріз S⁽ⁿ⁾a₁^і, a₂ⁱ,…,a_n-1ⁱ(jⁿ) містить не більше одного елемента a_nⁱ)ÎА_n.

Визначення. Якщо для будь-якої послідовності (а₁^і, a₂ⁱ,…,a_n-1ⁱ)Î
Î А₁´А₂´…´A_n-1 переріз S⁽ⁿ⁾а₁^і, a₂ⁱ,…,a_n-1ⁱ(jⁿ)-непорожній, то jⁿ є скрізь визначеним відношенням при відображенні його в бінарне відношення j² на множинах (А₁´ А₂´…´A_n-1) і А_n.

Визначення. Якщо переріз S⁽ⁿ⁾_X(jⁿ) по сукупності Х=А₁´А₂´…´А_n-1 дорівнює множині А_n, то jⁿ є сюр’єктивним відношенням при відображенні його в бінарне відношення j² на множинах

(А₁´ А₂´…´А_n-1) і А_n.

Визначення. Якщо для будь-яких двох послідовностей елементів (а₁^і, a₂ⁱ,…,a_n-1ⁱ),(а₁^j, a₂^j,…,a_n-1^j)ÎА₁´А₂´…´А_n-1 пересічення перерізів S⁽ⁿ⁾а₁^і, a₂ⁱ,…,a_n-1ⁱ(jⁿ)ÇS⁽ⁿ⁾а₁^j, a₂^j,…,a_n-1^j(jⁿ)=Æ, то jⁿ є ін’єктивним відношенням при відображенні його в бінарне відношення j² на множинах (А₁´ А₂´…´А_n-1) і А_n.

Відношення jⁿ є бієктивним при відображенні його в бінарне відношення j² на множинах (А₁´ А₂´…´А_n-1) і А_n, якщо jⁿ скрізь визначене, функціональне, ін’єктивне і сюр’єктивне при відображенні його в бінарне відношення j² на множинах (А₁´А₂´…´А_n-1) і А_n.

Приклад. Нехай існують множини А = {a, b}, B = {1, 2}, C = {I, II, III}. Тернарне відношення R³_A,B,C = {(a, 1, II), (b, 2, I), (a, 2, III), (b, 1, I ))} відображається у бінарне відношення R_(A,B),C = {((a, 1), II), ((b, 2), I), ((a, 2), III), ((b, 1), I)}, що є скрізь визначеним, сюр’єктивним, функціональним, неін’єктивним, і, отже, не бієктивним.

Визначення. Нехай jⁿ – функціональне відношення на множинах А₁,…,А_n при відображенні його в бінарне відношення j² на множинах (А₁´А₂´…´А_n-1) і А_n. Функція F_jn(x₁,…,x_n-1) називається зв'язаною з відношенням jⁿ, якщо кожна її змінна х_і приймає значення з множини А_і, де і=1, 2,…, n-1, а також F_jn(а₁, a₂,…, a_n-1)=S⁽ⁿ⁾а₁, a₂,…, a_n-1(jⁿ) для будь-якого набору (а₁, a₂,…, a_n-1)ÎА₁´A₂´…´А_n-1.

Приклад. Нехай тернарне відношення j³_A,B,C = {(a, 2, II), (b, 1, I),
(c, 1, III)} на множинах A = {a, b, c}, B = {1, 2}, C = {I, II, III} відображається у бінарне відношення j²_(A,B),C = {((a, 2), II),
((b, 1), I), ((c, 1), III)} на множинах A´B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)} і C = {I, II, II}. Тоді з відношенням j³ зв’язана функція F_j3(x₁, x₂), у якої x₁ÎA, x₂ÎB, x₃ÎC, F_j3(a,2)= S⁽³⁾a,2(j³)= II, F_j3(b,1)= S⁽³⁾b,1(j³)= I, F_j3(c,1)= S⁽³⁾c,1(j³)= III. Для інших наборів з A´B функція F_j3(x₁, x₂) дає Æ.

Якщо відношення j₁^m, j₂^m,…, j_n-1^m, jⁿ – функціональні і з ними зв'язані функції F_j1^m, F_j2^m,…,F_jn-1^m,F_jⁿ відповідно, то суперпозиція
jⁿ(j₁^m, j₂^m,…,j_n-1^m) також є функціональним відношенням. З суперпозицією jⁿ(j₁^m, j₂^m,…,j_n-1^m) зв'язана суперпозиція функцій
F_jⁿ(F_j1^m, F_j2^m,…,F_jn-1^m).

Лема. Суперпозиція скрізь визначених функціональних відношень також є скрізь визначеним функціональним відношенням.

Визначення. Відношення j називається відображенням множини А у В, якщо - функціонально й скрізь визначено, тобто для будь-якого аÎА Переріз… Елемент b=(a)j (або b=j(a)) називається образом елемента а в множині B при… Визначення. Сукупність всіх аÎА таких, що (а)j=b, називається повним прообразом елемента b в А при відображенні…

Лема. Відображення j множини А на множину В – взаємно однозначне (бієктивне), якщо воно також ін’єктивне.

Теорема. Відображення j множини А на множину В взаємо-однозначне (у цьому випадку множини А і В – еквівалентні) тоді і тільки тоді, коли j°j-1=dA, j… Наслідок. Якщо А=В, то відношення j - взаємно однозначне відображення множини… Приклад. Відображення j множини A = {a, b, c} на множину B = {1, 2, 3} з графіком jA,B ={(a, 3), (b, 1), (c, 2)} є…

Контрольні запитання

2. Які n-арні відношення є функціональними, ін’єктивними? 3. Які n-арні відношення є скрізь визначеними, сюр’єктивними? 4. Яка функція називається зв'язаною з n-арним відношенням jn?

Основна

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - с.43-46. 3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. –… 4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.97-115.

Вступ

Лекція має за мету навести поняття спеціальних бінарних відношень, що використовуються значно частіше за інші. Розглянуто еквівалентність, несуворий і суворий порядки, толерантність, квазіпорядок, а також множині властивостей спеціальних відношень. Звернено повагу на вигляд матричного, графового і множинного завдання спеціальних відношень.

У лекції присутні чотири підрозділи:

8.1. Еквівалентність

8.2. Порядок

8.3. Толерантність

8.4. Квазіпорядок

8.1. Еквівалентність

Визначення. Бінарне відношення r_А на множини А, що задовольняє властивостям рефлективності, транзитивності і симетричності, називається відношенням еквівалентності (~).

Очевидно, що якщо r_А - відношення еквівалентності на множині А, то обернене відношення r_А^-1 також є відношенням еквівалентності на даній множині.

Відношення еквівалентності на множині А зв'язано з розбивками цієї множини на попарно непересічні підмножини, що завдає належність кожного елементу множини А тільки одному класу розбивки.

Нехай r_А - деяке відношення еквівалентності на множини А, що не порожня. Розглянемо фактор-множину А/r_А={Sа(r_А)|аÎA}.

Визначення. Переріз S_a(r_A) називається суміжним класом елемента а по відношенню r_А.

Лема. Фактор-множина А/r_А по відношенню еквівалентності r_А є розбивкою множини А на суміжні класи ÈS_a(r_A)=A.

Тому що r_А – рефлексивно, справедливо аÎS_a(r_A) для кожного сÎA такого, що сÎS_a(r_A)ÇS_b(r_A), виконується аr_Ас і br_Ac, у силу симетричності аr_Aс і сr_Аb, у силу транзитивності аr_Ab і S_a(r_A)ÊS_b(r_A), у силу симетричності br_Aa і S_b(r_A)ÊS_a(r_A), тобто S_a(r_A)=S_b(r_A), таким чином різні суміжні класи не перерізаються.

Кожній розбивці R(A)={A₁, A₂,..., A_k} множини А відповідає відношення еквівалентності s_A на множині А, суміжні класи якого збігаються з класами даної розбивки, тобто аs_Ab тоді і тільки тоді, коли а,bÎA_і, де і=1, 2,..., k.

Теорема. Кожному відношенню еквівалентності на множині А відповідає єдина розбивка R(A) даної множини і, навпаки, будь-якій розбивці множини А однозначно відповідає деяке відношення еквівалентності на А.

Зв'язок відношень еквівалентності і розбивок множин можна використовувати при визначенні поняття кардинального числа, якщо вважати, що дві множини еквівалентні тоді і тільки тоді, коли вони рівно потужні. У цьому випадку кожному класу еквівалентності відповідає визначена потужність (кардинальне число), причому деякому класу розбивки скінченних множин відповідає натуральне число - число елементів у множинах з даного класу.

Нехай r - відношення еквівалентності на множини А, A/r={S_a(r)/aÎA} - фактор-множина множини А по даному відношенню еквівалентності.

Визначення. Відображення множини А на фактор-множину А/r, що зіставляє кожному елементу аÎA суміжний клас S_a(r), якому належить елемент а, називається природним відображенням множини А на фактор-множину А/r.

Нехай j - відображення множини А на множину В. Відображенню j відповідає деяке цілком визначене відношення еквівалентності s на множині А. Нехай для елементів а₁, а₂ÎA а₁sа₂ тоді і тільки тоді, коли (а₁)j=(а₂)j. При зіставленні кожному елементу bÎB його повного прообразу при відображенні j виходить взаємно однозначне
відображення y множини В на фактор-множину А/s, причому композиція j°y збігається з природним відображенням множини А на фактор-множину А/s.

Всі елементи, що належать деякому класу А_і розбивки R={A₁,..., A_n} множини А, зв'язані відношенням еквівалентності і взаємозамінні у тому сенсі, що кожний з цих елементів визначає даний клас, тобто може служити його представником (еталоном).

Визначення. Підмножина множини А, що містить по одному і тільки одному елементу а_і з кожного класу А_і деякої розбивки Р={A₁, A₂, ... , A_i,..., A_n} множини А, називається системою представників відповідного відношення еквівалентності.

Приклад. а) Нехай є множини А = {а₁, а₂, а₃} і B = {b₁, b₂, b₃,b₄ b₅, b₆, b₇}. Р₁={а₁, а₂, а₃}, r_А,1={<а₁, a₁>, <a₁, a₂>, <a₁, a₃>, <a₂, a₁>, <a₂, a₂>, <a₂, a₃>,<a₃, a₁>,<a₃, a₂>, <a₃, a₃>}; P₂={{a₁}, {a₂}, {a₃}}, r_A,2={<a₁, a₁>, <a₂, a₂>, <a₃, a₃>}; P_B={{b₁, b₂, b₃}, {b₄}, {b₅, b₆, b₇}}; r_B={(b₁, b₁), (b₁, b₂), (b₂, b₁), (b₂, b₂), (b₁, b₃),
(b₃, b₁), (b₃, b₃), (b₂, b₃), (b₃, b₂), (b₄, b₄), (b₅, b₅), (b₅, b₆), (b₆, b₅), (b₆, b₆), (b₅, b₇), (b₇, b₅), (b₇, b₇), (b₆, b₇), (b₇, b₆)}

б) Таблиця 8.1.

rB	b1	b2	B3	b4	b5	B6	b7
b1	1	1	1
b2	1	1	1
b3	1	1	1
b4				1
b5					1	1	1
b6					1	1	1
b7					1	1	1

в)

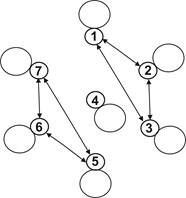
Рис. 8.1. Відношення еквівалентності r_B

8.2. Порядок

Визначення. Бінарне відношення r_А на деякій множини А, що задовольняє властивості рефлективності, транзитивності і антисиметричності, є відношенням несуворого порядку (³_А).

Множина А з визначеним на ньому відношенням несуворого порядку r називається несуворо впорядкованою. Елементи a, bÎA такі, що a³b чи a£b, називаються порівнянними елементами несуворо упорядкованої множині, у несуворо впорядковану множину можуть входити і непорівнянні елементи.

Несуворо упорядкована множина, у якой кожна пара елементів порівнянна, називається зовсім чи лінійно упорядкованою чи множиною ланцюгом. У цьому випадку має місце лінійний несуворий порядок. Таким чином, відношення несуворого порядку лінійно тоді і тільки тоді, коли воно зв’язано, у противному випадку відношення несуворого порядку називається нелінійним.

Відношення ²£² на множині А дозволяє визначити відношення ²<² як таке, що для а, bÎA a<b тоді і тільки тоді, коли а£b і а¹b.
Відношення ²<² на множині А називається відношенням суворого порядку і має властивості антирефлексивності, сильної антисиметричності, транзитивності. Відношення ²<² на множині А дозволяє у свою чергу однозначно визначити відношення ²£² на даній множині ²£²=²<²Èd_A і ²<²=²£² d_A. Для суворого порядку також вводяться поняття суворо впорядкованої множини, порівнянних елементів, лінійного суворого порядку (властивість зв’язності) і часткового суворого порядку.

Приклад.Відношення несуворого порядку ²бути дільником² на множини {1, 2, 3, 4, 5, 6, 7}

а) Таблиця 8.2.

	1
	1	1
	1		1
	1	1		1
	1				1
	1	1	1			1
	1						1

б)

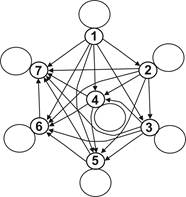
Рис. 8.2. Відношення несуворого порядку

Нехай Р(А²) - множина усіх бінарних відношень, визначених на деякій множині А. Нехай ²£² - бінарне відношення на множині Р(А²) таке, що для відношень r,sÎР(А²) справедливо r£s тоді і тільки тоді, коли з аrb випливає аsb, де а,bÎA, тобто для всіх графіків r_А і s_А виконується включення r_AÍs_A. Таким чином, множина Р(А²) є частково упорядкованою щодо відношення ²£² .

Нехай Т(А²)ÍR(A²) - сукупність усіх відношень еквівалентності на множині А. Визначена часткова упорядкованість ²£² на множині Р(А²) індукує часткову упорядкованість на множині Т(А²), в такому разі якщо характеризувати відношення еквівалентності відповідними їм розбивками множини А, то r£s означає, що розбивка А/r={S_a(r)/aÎA} більш дрібна, ніж розбивка А/s={S_a(s)/aÎA}, тобто для кожного суміжного класу S_a(s)Î/s існує розбивка R(S_a(s))={S_a¢(r)|a¢Î S_a(s)}ÍA/r. У цьому випадку розбивка А/r зветься підрозбивкою розбивки А/s.

Нехай F(А)=А* - множина усіх слів (векторів) скінченної довжини в алфавіті (множині) А и на множини А задане відношення часткового (суворого) порядку.

Лема. Для двох векторів В,СÎF(A) вектор В несуворо передує вектору С тоді і тільки тоді, коли довжина вектора В дорівнює довжині вектора С, тобто ½С½=½B½ і кожен компонент b_i вектора В – не суворо передує відповідному компоненту с_і
вектора С. Вектор В суворо передує вектору С, якщо і тільки якщо одночасно з виконанням відношення несуворого передування існує принаймні один компонент b_i вектора В, що є суворо попереднім компоненту c_i вектора С.

Приклад. А={1, 2, 3}, А³ - множина векторів довжини 3.

<1, 2, 3> £ <1, 2, 3>; <1, 2, 3>£<1, 3, 3>;
<1, 2, 3> < <2, 2, 3>; <1, 2, 3>_>|^< <2, 1, 3>.

Лема. Відношення несуворого (суворого) передування на множині векторів є відношення несуворого (суворого) порядку на множині векторів скінченної довжини.

Нехай F(A)=А* - множина усіх слів (векторів) скінченної довжини в алфавіті (множині) А и на множині А задане відношення лінійного суворого порядку. У цьому випадку можна ввести лексіграфічний порядок на множині F(A), який може визначатися як ²í².

Для двох векторів В, СÎF(A) вектор В лексіграфично передує вектору С (ВíС) тоді і тільки тоді, коли виконується одне з двох умов:
а) існує таке і, де 1£ і £min (½B½, ½C½), що для всіх 1£j£і виконується b_j=c_j, але b_i<c_i; б) для всіх і, де 1£і£mіn (½B½, ½C½), b_i=c_i, але ½B½<½С½.

Приклад.Слова лісíліто; борíборовик, впорядковані в словнику.

8.3. Толерантність

Визначення. Відношення r на множині А називається відношенням толерантності, якщо воно рефлексивно і симетрично.

Синонімом толерантності є сумісність. Для відношення толерантності на відміну від відношення еквівалентності транзитивність не обов'язкова, отже, відношення еквівалентності - окремий випадок відношення толерантності.

Визначення. Класом сумісності називається підмножина А¢ÍA така, що будь-які два елементи а₁ і а₂, їй належні, є толерантними.

Клас сумісності називається максимальним, якщо він не є підмножиною ніякого іншого класу сумісності. Різні класи можуть містити однакові елементи, отже, є множинами, що Перерізають.

Теорема. Усяке відношення толерантності r на множині А задає покриття множини А, блоки покриття при цьому є і класами сумісності і, навпаки, усяке покриття множини А підмножинами з {A₁, А₂,..., А_n} визначає між елементами кожного з підмножин покриття деяке відношення толерантності.

Покриття множини може бути не єдиним, у зв'язку з чим важливе значення має пошук покрить з мінімальним, з урахуванням повторень, числом елементів у ньому, називаний задачею визначення мінімального покриття. Очевидно, що у випадку відношення еквівалентності абсолютно мінімальним покриттям є розбивка - мінімальне сумарне число елементів у ньому дорівнює потужності множини ½A½.

Приклад. А={пол, лицо, кит, море, мина}. Пари слів належать відношенню r, якщо вони мають загальну букву.

а) Таблиця 8.3.

	1	1		1
	1	1	1	1	1
		1	1		1
	1	1		1	1
		1	1	1	1

б)

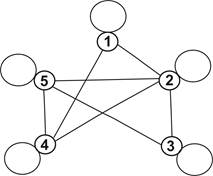
Рис. 8.3. Відношення толерантності:

в) {1, 2, 4}, {2, 3, 5}, {2, 4, 5} - максимальні класи сумісності, {1, 2}, {2, 4}, {2, 5}, {3, 5}, {4, 5} - не максимальні.

Покриття {{1, 2, 4}, {2, 3, 5}, {2, 4, 5}} взаємно однозначно відповідає відношенню толерантності r={(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 2), (2, 1), (1, 4), (4, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (3, 5), (5, 3), (4, 5), (5, 4)}.

8.4. Квазіпорядок

Визначення. Відношення r на множини А називається відношенням квазіпорядку, якщо воно рефлексивно і транзитивне.

Синонімом квазипорядку є передпорядок і передупорядкування.

Для відношення квазіпорядку на відміну від відношень еквівалентності і часткового порядку властивості відповідно симетричності й антисиметричності не обов'язкові, отже, відношення еквівалентності і часткового порядку - окремі випадки відношення квазіпорядку.

Приклад. Відношення подільності на множини цілих чисел (позитивних, негативних і нуля) є відношенням квазіпорядку

а) Таблиця 8.4.

	-1
-1

б)

Рис. 8.4. Відношення квазіпорядку

Контрольні запитання

2. Якій зв’язок між розбивками і відношенням еквівалентності? 3. Що є фактор-множиною А/rА, і суміжним класом елемента а по відношенню rА? … 4. Що є природним відображенням множини А на фактор-множину А/r і системою представників відповідного відношення…

Основна

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.46-64. 3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. –… 4. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.115-137.

Вступ

Лекція має за мету навести поняття замикань, спеціальних функцій і операцій. Розглянути транзитивне і рефлексивне замикання відношень і отримання замикань за допомогою методу Варшалла. Також розглянути спеціальні функції: підстановки, послідовності, функціонали та функції, що зберігають алгебраїчні властивості і структури. Звернено повагу до операцій, у тому разі і до інфіксної, префіксної та постфіксної форм запису операцій, а також до властивостей операцій.

Лекція містить три підрозділи:

9.1. Замикання відношень

9.2. Спеціальні функції

9.3. Операції

9.1. Замикання відношень

Визначення. Транзитивним замиканням R⁺ відношення R називається Перетин всіх транзитивних відношень, що містять R як підмножину.

Визначення. Рефлексивним (і транзитивним) замиканням R* відношення R називається Перетин всіх рефлексивних і одночасне транзитивних відношень, що містять R як підмножину.

Справедливі рівності:

1. R*=E_AÈR⁺

2. R⁺={(х, у)ÎA²|в графі відношення R існує шлях з х в у}.

Слід зазначити, що перетин R⁺ є транзитивним відношенням, а R* - рефлексивним і транзитивним. Якщо множина А кінцева, то рефлексивне і транзитивне замикання відношення R може бути отримане за допомогою методу Варшалла:

рефлексивне замикання: R*=R₀ÈRÈ(R°R)ȼÈ(R°R°¼°R),

транзитивне замикання: R⁺=RÈ(R°R)ȼÈ(R°R°¼°R)

де R₀=E_A, ½A½=n, в останній операції композиції присутні n членів-відношень R.

Визначення. Нехай А - множина, nÎN і g=(Aⁿ, A, G) - відповідність. Підмножина А¢ множини А називається замкнутою щодо відповідності g, якщо g((А¢)ⁿ)ÍA.

Лема. Для кожної підмножини А¢ множини А існує єдина підмножина А² множини А, що є найменшою надмножиною відносно А¢ і що замкнута до відповідності g, така надмножина А² зветься g-замиканням А¢ чи замиканням А¢ відносно g.

Лема. Справедлива рівність А²=Ç{A^|А¢ÍA^ і множина А^ - замкнута відносно відповідності g}, тому що, якщо А¢ÍA^ÍA і А^ - замкнута відносно g, то А²ÍA^.

Однозначність g-замикань використовується при індуктивних визначеннях, щоб задати деяку множину А, елементи якої задовольняють дані умови, цілком описують деяку підмножину А¢ цієї множини і визначають усю множину А як замикання А¢ щодо деяких операцій.

Приклад. М=Р(А) і g=(М², М, G) - така відповідність, що кожним двом підмножинам А¢ і A² множини А зіставляє три множини А¢ÈA², А¢ÇA² і А¢А². Сім’я множин, що містить Æ і всі скінченні підмножини множини А замкнути відносно g.

Приклад.А=В² і g=(А², А, {(((х, у), (у, z)), (х , z)) | х, у, z ÎB}). Для будь-якого відношення r на В у цьому випадку r⁺ - замикання r відносно g.

9.2. Спеціальні функції

Підстановки

Число різних підстановок для скінченних множин можна легко обчислити. Нехай ½A½=nÎN і нехай nPn - число таких підстановок.… Нехай y - підстановка Nn, тоді y можна визначити як множину n пар y={(1, x1), (2, x2),..., (n, xn)}, де (x1, x2,...,…

Послідовності

Визначення. Послідовністю на множини А називається відображення N в А.

Якщо s:N®A - задана послідовність і s(n)=a_n, то звичайно позначають послідовність не s, а (а_n) чи (а₁, а₂,..., а_n,...). У цьому випадку а_n називають n-м членом послідовності.

Приклад. s:N®A і s = {(1, червоний), (2, оранжевий), (3, жовтий), (4, зелений), (5, блакитний), (6, дуже блакитний), (7, фіолетовий)}.

Функціонали

Визначення. Функція f:A®[B®C] називається функціоналом, тобто для будь-якого аÎA f(a) - функція - f(a):B®C, для будь-якого bÎB… Необхідно мати на увазі, що множини функцій [B®С] можуть розглядатися як і… Приклад. Нехай функція f:A®[B®C] визначає терміновість кореспонденції, функція - f(a):B®C – вибір транспортного засобу…

Функції, що зберігають алгебраїчні властивості

Визначення. Нехай X і U - множині, а rx і rу – деякі відношення на них і нехай f:X®U - таке відображення, що з відношення x1rxx2 випливає відношення… Найпростіший приклад - для еквівалентності. Приклад. Нехай X і U - множині, а rx і rу - відношення еквівалентності на них і нехай f:X®U - відображення. Нехай далі…

Загальні визначення операцій

Визначення. Операцією над множиною S називається функція f: Sn®S, де nÎN і є два важливих моменти операції: а) однозначність… Операція Sn®S має порядок n. Якщо n=1, то операція одномісна (унарна,… Приклад. Бінарною операцією є додавання, або добуток на множині дійсних чисел D, унарною операцією є ступень на…

Контрольні запитання

2. У чому суть методу Варшалла? 3. Яка підмножина А¢ множини А називається замкнутою щодо відповідності… 4. Що є підстановкою, циклом? Які елементи є стаціонарними?

Основна

2. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.64-68. 3. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. –… Додаткова

Внутрішній закон композиції

10.2.1. Властивості внутрішнього закону Операції на множині S можуть мати деякі загальні властивості, які звичайно… Комутативність а Т b = b Т а

Контрольні запитання

2. Що називають законом композиції? 3. У чому розходження між зовнішнім й внутрішнім законами композиції? 4. Що розуміють під групоїдом?

Список літератури

1. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.137-141. 2. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. -… 3. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учеб. Для вузов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. -…

Групи підстановок і кільце множин

11.2.1. Групи підстановок Розгляд деяких систем можна почати із групи підстановок, загального опису яких… Визначення. Композиція (добуток) підстановок а й b — це композиція двох взаємно однозначних відображень множини…

Теорема Кели. Усяка кінцева група порядку n може бути представлена групою підстановок n-го ступеня її елементів.

Таблиця 11.8 T x1 x2 x3 x1 …

Контрольні запитання

2. Що розуміють під кільцем? Які кільця можливі? 3. Що додає до кільця тіло, поле? 4. Яка різниця між системою й підсистемою?

Список літератури

1. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975ю - С.141-152. 2. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. -… 3. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учеб. Для вузов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. -…

Вступ

Лекція має за мету висвітлити початкові поняття комбінаториці. Розглянуто вибірку елементів, правила суми та добутку. Звернена увага до базових методів перестановки, сполучення, рекурентних співвідношень, а також бінома Ньютона.

У лекції присутні шість параграфів:

12.1. Вибірка елементів

12.2. Правило суми і добутку

12.3. Перестановки

12.4. Сполучення

12.5. Рекурентні співвідношення

12.6. Біном Ньютона

Вибірка елементів

Приклад. Нехай, наприклад, дана множина M = {a,b,c,d}. Вибірки abc, acb, bac, bca, cab, cba є різними 3-перестановками, утвореними з тих самих… Вибірки можуть допускати і не допускати повторення елементів. При вибірках з… У першому випадку передбачається, що запас повторюваних елементів обмежений і визначається специфікацією {,......,},…

Правило суми і добутку

Правило суми. Якщо об'єкт a може бути обраний p способами, а об'єкт b - іншими q способами, то вибір “або a, або b” може бути здійснений p+q… Вибори a і b взаємно виключають одне одного. Необхідно, щоб не один зі… Правило добутку. Якщо об'єкт a може бути обраний p способами і після кожного з таких виборів об'єкт b у свою чергу…

Перестановки

Перестановки. Перший член перестановки можна вибрати з n елементів n способами – елементи не повинні повторюватися, вибір другого члена можна… Застосовуючи послідовно правило добутку, одержуємо p(n,r) = n (n-1)......(n – r + 1), n r.

Сполучення

r-сполучення з n різних елементів: З кожного такого сполучення можна утворити r! перестановок, тому число r-сполучень з n різних елементів буде в r!… C(n, r) = = = Приклад. З чотирьох різних об'єктів, що позначаються 1, 2, 3, 4, можна скласти таки шість сполучень по два елементи…

Рекурентні співвідношення

Рекурентні співвідношення. Множину r-перестановок з n різних елементів можна розбити на два класи так, що перестановки одного з них не містять… P(n, r) = P(n-1, r) + r(n-1, r-1) Символ P(k, 0), що не має комбінаторного змісту, прийнято вважати дорівнюючим одиниці. P(k, 1) = k для будь-якого…

Біном Ньютона

(1+... = Коефіцієнт багаточлена являє собою суму добутків, кожний з яких є утворений r… Біномом Ньютона і біноміальні коефіцієнти. Якщо покласти , то будь-Якій добуток r-сполучень елементів дорівнює одиниці…

Контрольні запитання

2. Що є r-сполученням? 3. Що таке специфікація та сімейство представників? 4. У чому полягає правило суми і добутку?

Основна

2. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.169-174. 3. Иванов Б.Н. Дискретная математика. Алгоритмы и программы: Учебное пособие.… Додаткова

Вступ

Лекція має за мету навести додаткові комбінаторні методи. Повернута увага до поліноміальних та експонентних твірних функцій, що узагальнюють біном Ньютона, принцип включення і виключення та розбивок.

У лекції присутні чотири підрозділи:

13.1. Поліноміальні функції, що виробляють

13.2. Експонентні функції, що виробляють

13.3. Принцип включення і виключення

13.4. Розбивки

Поліноміальні твірні функції

Якщо об'єкт може входити в сполучення 0, 1,...,k раз, то замість 1+треба взяти співмножник 1+(при k=0 співмножник дорівнює одиниці). Тоді при… Приклад. Для r-сполучення з трьох елементів a, b, c зі специфікацією {3, 1, 2}… Поліноміальна твірна функція (энумератор). Багаточлен вигляду називають поліноміальною функцією, або твірною…

Експонентні твірні функції

, тобто число r-перестановок з різних елементів є коефіцієнтом при у розкладанні… Експонентні твірні функції. Визначимо твірну функцію для r-перестановок з необмеженими повтореннями так, щоб U(n, r) =…

Принцип включення і виключення

Нехай є N об'єктів і деяка сукупність властивостей . Позначимо через N, N, Nі т.д. кількість об'єктів, що мають відповідно властивостями і т.д.… Формула включення і виключення. Число об'єктів, що не мають жодним із…

Розбивки

Приклад. Для числа 4 є 5 розбивок без обмежень. (4, 31, 22, 211, 1111) і вісім розбивок з урахуванням порядку частин (4,31, 13, 22, 211, 121, 112,… Якщо прийняти як твірну функцію для розбивки числа п без обмежень р(п)… р (х) = (1+х+

Контрольні запитання

2. Що є більш загальним – біном Ньютона чи енумератор? 3. Що таке експоненціальна твірна функція? 4. Що проголошує принцип включення і виключення?

Основна

2. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.174-182. 3. Иванов Б.Н. Дискретная математика. Алгоритмы и программы: Учебное пособие.… Додаткова

РОЗДІЛ III. ГРАФИ

Лекція 14. Визначення і представлення графів

Вступ

Лекція має за мету навести базові визначення і поняття теорії графів. Розглянути висловлення, визначення та компоненти графів, неорієнтовані та орієнтовані графи, спеціальні види графів, способи завдання неорієнтованих та орієнтованих графів. Звернено увагу до визначення ізоморфних графів.

У лекції присутні два підрозділи:

14.1. Основні визначення

14.2. Способи представлення графів

Основні визначення

Визначення. Множина вершин Х, що зв'язані між собою множиною ребер V, називається графом і позначається G = <X,V>. Приклад. Граф (рис. 14.1) G = <{x1, x2, x3, x4}, {v1, v2, v3, v4, v5}> …  

Рис. 14.5. Мультиграф і псевдограф

Граф, що не має ребер, усі вершини якого ізольовані, називається порожнім чи нуль-графом. Простий граф, у якому дві будь-які вершини з'єднані ребром, називається повним.

 

Рис. 14.6. Повний граф

Якщо вершини Х простого графу допускають таку розбивку на дві непересічних підмножини Х1 і Х2 (Х1 Ç Х2 = Æ і Х1 È Х2 =Х), що не мають ребер, які з'єднують вершини тої самої підмножини, то він називається двочастковим чи біграфом.

Приклад. Біограф (рис. 14.7), у якому X = {x1, x2, x3, x4, x5, x6}, X1 = {x1, x2, x3}, X2 = {x4, x5, x6}

Рис. 14.7. Двочастковий граф (біграф)

Граф, ступені вершин якого однакові і рівні “r”, називається однорідним, чи регулярним r-го ступеня.

Рис. 14.8. Однорідні графи

Дві вершини x_i і x_j Î X графу G = <X, V> називають суміжними, якщо вони з'єднані ребром v_kÎ V. Для неорієнтованого графу суміжним вершинам відповідає дві пари <x_i, x_j> і <x_j, x_i>, для орграфу це пари
<x_i, x_j>, причому x_i - початок дуги, x_j - кінець дуги. Вершина x_i і ребро (дуга) v_k інцидентні, якщо ребро (дуга) входить (виходить) з вершини x_i.

Способи представлення графів

Більш складний аналітичний спосіб завдання відзначених графів у вигляді трійки G=<X, V, D>, де D - відношення, що задається у свою чергу… Інший основний спосіб - завдання графу G за допомогою матриці. У матриці… Приклад. Орієнтований граф, заданий матрицею суміжності і графічно

Рис. 14.13. Ізоморфні графи

Принципово можливо в матриці інцидентності визначити також і петлі графу чи орграфу - у цьому випадку для неорієнтованого графу на перетинанні i-го рядка, що відповідає вершині x_i, і j-го стовпця, що відповідає ребру-петлі v_j, ставиться двійка, для орграфу на перетинанні
i-го рядка і j-го стовпця необхідно, наприклад, вказати одночасно як +1, так і -1.

Для модифікованої в такий спосіб матриці інцидентності справедливі усі твердження, що стосуються звичайної матриці інцидентності.

Контрольні запитання

2. Що є неорієнтованим і орієнтованим графами? 3. Що є ребром, дугою, петлею, рівнобіжними ребрами, строго і нестрого… 4. Що є ступенем, напівступенем заходу і напівступенем виходу?

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.189-194. 3. Кук Л., Бейз Г. Компьютерная математика. – М.: Наука, 1990, с.217-224. 4. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.89-94.

Вступ

Лекція має за мету навести додаткові поняття теорії графів. Розглянути визначення маршрутів, ланцюгів, ейлерових та гамільтонових обходів, зв’язності, початкової та скінченної вершин, точок зчленування, дерев, ексцентриситету, радіуса, центра та зважених графів. Звернено увагу до прикладів визначень.

У лекції присутні два підрозділи:

15.1. Основні визначення (продовження)

15.2. Зважені (відзначені) графи

15.1. Основні визначення (продовження)

Визначення. Маршрут (шлях) довжини m визначається як послідовність ребер графу, не обов'язково різних, у яких, що граничні вершини двох сусідніх ребер збігаються.

Замкнутий маршрут приводить до тієї ж вершини, з якої він починається. Маршрут позначається як М = <v₁, v₂,…,v_j,…,v_n>...

Приклад. Неорієнтований граф (рис. 21.1.) і можливі маршрути M¹_{x1 « x4} = <v1, v2, v3, v2, v4, v5>, M² _{x1 « x4}= <v6>

 

Рис. 15.1. Неорієнтований граф

Визначення. Довжиною маршруту (шляху) М = <v₁, v₂,…,v_j,…,v_n> називається число дуг, що його складують.

Довжина маршруту позначається l(M).

Приклад. Для рис. 15.1. замкнуті маршрути M_{x1 « x1} = <v1, v2, v5, v6>; M¹_{x3 « x3} = < v4>; M² _{x3 « x3}= < v3, v2>.

Визначення. Маршрут, усі ребра якого різні, зветься ланцюгом, маршрут, для якого різні усі вершини, що він проходить, називається простим ланцюгом.

Приклад. Для рис. 15.1. M_{x1 « x1} = <v1, v2, v5, v6> і M_{x1 « x4} = <v1, v2, v4, v5> - ланцюги, M_{x1 « x4} = <v1, v2, v5> - простий ланцюг.

Замкнутий ланцюг звється циклом, замкнутий простий ланцюг називається простим циклом.

Приклад. M_{x1 « x1} = <v1, v2, v4, v5, v6> і M_{x3 « x3} = <v3, v2, v4> - цикли, M_{x1 « x1} = <v1, v2, v5, v6> та M_{x1 « x1} = <v3, v2 > - прості цикли.

Визначення. Цикл графу, що містить усі його ребра, називається ейлеревим циклом.

Визначення. Простий цикл графу, що проходить через усі його вершини, називається гамільтоновим циклом.

Ейлерів і гамільтонів цикли (обходи) можливі не для будь-якого графу чи орграфу. В орграфі при визначенні маршруту, ланцюга, циклу, ейлерева і гамільтонова циклу природно враховується напрямок дуг.

Визначення. Частина графу, що містить поряд з деякою підмножиною ребер і всі інцидентні їм вершини, називається підграфом.

Приклад. Граф G = <X, V>, де X = {x1, x2, x3, x4}, V = {v1, v2, v3, v4, v5} і підграф G' = <X’, V'>, де X’ = { x2, x3, x4}, V' = { v2, v3, v4}, G' Ì G, Х' Ì X, V' Ì V.

Рис. 15.2. Граф (ліворуч) і підграф (праворуч)

Визначення. Входом чи початковою вершиною орграфу G = <X, V> є вершина x^(s)Î X, у якій p(x^(s)) = 0, виходом чи кінцевою вершиною орграфу G = <X, V> є вершина x^(F)Î X, у якій s(x^(F)) = 0.

Приклад. Початкова вершина x₁ і скінченні вершини x₃, x₅

 

Рис. 15.3. Початкові і скінченні вершини (х1 – вхід, х3, х5 - вихіди)

В орграфу може бути кілька входів чи виходів (х₅ - другий вихід).

У загальному випадку як вхід чи вихід графу можна розглядати довільну (призначену за якім-небудь критерієм) вершину, а саме, якщо умова входу чи виходу не виконуються, тобто `$xi(p(xi) = 0) чи `$xi(s(xi)= = 0), то виводиться фіктивна вершина x^(S)Ï X чи x^(F) Ï X, що з'єднується єдиною дугою до заданої вершини чи единою дугою із заданої вершини.

Приклад. Уведення фіктивних вершин

Рис. 15.4. Уведення початкової (вхід x_s) і скінченної (вихід x_f) вершин

Шлях від входу орграфу до його виходу, тобто від вершини x^(S) до його вершини x^(F)називається x^(S) - x^(F) - шляхом. Вважається, що хоча б один такий шлях в орграфі існує.

Якщо в орграфі вершини x_i і x_j зв'язані шляхом M[x_i, x_j], то вершина x_j досяжна з вершини x_i чи що вершина x_i досягає вершини x_j.

Дві вершини графу називаються зв'язними, якщо існує маршрут, що їх з'єднує, інакше - незв'язними.

Визначення. Орграф називається міцно зв’язаним, якщо для будь-якої пари його вершин x_i, x_j Î X існує орієнтований шлях як з x_i у x_j , так і з x_j у x_i.

Визначення. Граф називається зв'язним, якщо для будь-якої пари його вершин x_i , x_j Î X існує шлях з x_i у x_j чи шлях з x_j у x_i.

Визначення. Орграф називається слабо зв’язним, якщо для будь-якої пари його вершин x_i, x_j Î X існує така вершина x_k, що x_k досягає як x_i, так і x_j, чи x_k досяжна як з x_j, так і з x_i.

Визначення. Граф, що не є ні міцно зв’язним, ні зв'язним, ні слабо зв’язним називається незв'язаним графом.

Приклад. Зв'язний граф і міцно зв’язний орграф

 

Рис. 15.5. Зв'язаний граф (ліворуч) і міцно зв'язаний орграф (праворуч)

Якщо існує така вершина, видалення якої перетворює зв'язний граф в незв'язаний, то вона називається точкою зчленування, ребро з такими ж властивостями називається мостом.

Визначення. Граф називається нероздільним, якщо він зв'язний і не має точок зчленування, граф, що має хоча б одну точку зчленування є роздільним і називається сепарабельним.

Приклад. Граф з однією точкою зчленування і граф з одним мостом

 

Рис. 15.6. Точка зчленування і міст

Зв'язані ациклічні графи називаються деревами. Дерева містять мінімальну кількість ребер, що забезпечує зв'язаність графу. Незв'язаний граф, компонентами якого є дерева, називається лісом.

Приклад. Дерева з різним розгалуженням

 

Рис. 15.7. Дерева

Нехай |X| і |V| - кількості вершин і ребер. Для дерев справедливо:

|X| = |V| + 1; |V| = |X| - 1

Визначення. Граф називається плоским (планарним), якщо існує ізоморфний йому граф, що може бути зображений на площині без перетину ребер.

Нехай відстанню d(x₁, x₂) між вершинами x₁, x₂ у дереві (графі) називається довжина мінімального шляху з x₁ у x₂. Відстань від вершини х до найбільш віддаленої від її вершини називається ексцентриситетом е(х) вершини х, тобто

е(х) = max(d(x, y)) = max(È d(x, y))

^{y yÎ X}

Найменший з ексцентриситетів називається радіусом r(T) дерева

r(T) = min(e(x)) = min(Èe(x))

^{x xÎX}

Центральною вершиною дерева Т називається вершина, у якій ексцентрисітет дорівнює радіусу. Центром дерева називається множина його центральних вершин. Кожне дерево має центр, що складається з однієї вершини чи двох суміжних вершин.

Приклад. r(T) = 3, e(x) = 6 графу

 

Рис. 15.8. Радіус дерева і ексцентриситети вершин дерева

Зважені (відзначені) графи

Вага дуги чи ребра може означати довжину, пропускну здатність, напругу чи струм і т. д. Ваги можна приписувати не тільки ребрам (дугам), але і… Приклад. Матриця суміжності і графічне представлення зваженого орграфу  

Контрольні запитання

2. Що є ланцюгом, простим ланцюгом, циклом, простим циклом? 3. Яка різниця між ейлеревим та гамільтоновим циклами? 4. Що є підграфом, яка різниця між початковою та кінцевою вершинами?

Основна

2. Кук Л., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.224-257. 3. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001.… Додаткова

Вступ

Лекція має за мету навести поняття теоретико-множинних операцій над графами. Розглянути визначення об’єднання, перетину, доповнення, різниці, декартова добутку і композиції графів, а також десять загальних властивостей базових операцій. Звернено увагу до упорядкованості компонентів графів і операцій над компонентами, яка відрізняє графові операції від звичайних множинних.

У лекції присутні два підрозділи:

16.1. Операції над графуми

16.2. Властивості операцій над графуми

Операції над графами

Визначення. Об'єднанням Q = GÈH називається граф Q = <A, S> такий, що A = XÈY, а S = ГÈР. Приклад : Граф G, для якого X = {x1, x2, x3}, Г = {<x1, x2>, <x1, x3>, <x2, x2>, <x3, x2>};…

Властивості базових операцій над графами

GÈH = HÈG; GÇH = HÇG; комутативність

GÈ(HÈF) = (GÈH)ÈF; GÇ(HÇF) = (GÇH)ÇF; асоціативність

GÈ(HÇF) = (GÈH)Ç(GÈF); GÇ(HÈF) = (GÇH)È(GÇF); дистрибутивність

GÈGÆ = G; GÇGÆ = GÆ; GÈGU = GU; GÇGU = G; властивості меж

GÈG = G; GÇG = G; ідемпотентність

GÈ`G = GU; GÇ`G = GÆ; доповнення

GÈ(GÇH) = G; GÇ(GÈH) = G; поглинання

GÈH)Ç(GÈ`H) = GÈHÆ; (GÇH)È(GÇ`H) = GÇHU; склеювання

GÈ(`GÇF) = GÈ(GUÇF); GÇ(`GÈF) = GÇ(GÆÈF); Блейка-Порецького

Ugrave;(GÈH) = `GÇ`H ù(GÇH) = `GÈ`H де-Моргана

Визначення. Декартовим добутком Q = G´H графів Q = <X, Г> і
Н = <Y, P> називається новий граф Q = <A, S>, де A =X´Y і для будь якого <x, y>ÎA виконується S(<x, y>) =Г(x)´P(y)).

Приклад : Для графів G =<X, Г>, H = <Y, P>, у яких X = {x1, x2},
Г ={<x1, x1>, <x2, x1>, <x2, x2>} і Y = {y1, y2}, P = {<y1, y1>, <y1, y2>, <y2, y1>}, а також Г(x1)= = {x1}, Г(x2) = {x1, x2}, P(y1) = {y2, y1}, P(y2) = {y1}, множина вершин графу Q =
= <A, S> і множина переходів рівні:

A = X´Y = {a1, a2, a3, a4} = {<x1, y1>, <x1, y2>, <x2, y1>, <x2, y2>}, S(<x1, y1>) = Г(x1)´P(y1) = {<x1, y1>, <x1, y2>}, S(<x1, y2>) = Г(x1)´P(y2) = {<x1, y1>}, S(<x2, y1>) = F(x2)´P(y1) = ={<x1, y1>, <x1, y2>, <x2, y1>, <x2, y2>}, S(<x2, y2>) = =Г(x2)´P(y2) = {<x1, y1>, <x2, y1>}

 

 

Рис. 16.5. Декартів добуток графів Q = G´H

Визначення. Композицією Q = G ° H графів G = <Х, Г> і H =<Y, P> називається граф Q = <A, S>, де A = X´Y і для <x, y>ÎA виконується S(<x, y>)) ={Г(x)´Y}È{X´P(y)}).

Приклад. Для графів G = <X, Г>, H = <Y, P>, у яких X = {x1, x2},
Г = {<x1, x1>, <x2, x1>, <x2, x2>} і Y = {y1, y2}, P = {<y1, y1>, <y1, y2>, <y2, y1>},

а також Г(x1)={x1}, Г(x2)={x1, x2}, P(y1)={y2, y1}, P(y2)={y1},

множина вершин графу Q = <A, S> і множина переходів рівні

A = X´Y = {a1, a2, a3, a4} = {<x1, y1>, <x1, y2>, <x2, y1>, <x2, y2>}, S(<x1, y1>) = {{x1}´{y1, y2}}È{{x1, x2}´{y1, y2}} = {a1, a2, a3, a4}, S(<x1, y2>) = {{x1}´{y1, y2}}È{{x1, x2}´{y1}} = {a1, a2, a3}, S(<x2, y1>) = {{x1, x2}´{y1, y2}}({{x1, x2}´{y1, y2}} = {a1, a2, a3, a4}, S(<x2, y2>) = {{x1, x2}´{y1, y2}}È{{x1, x2}´{y1}} = {a1, a2, a3, a4}.

 

Рис. 16.6. Композиція графів Q = G ° H

 

Контрольні запитання

2. Які властивості має об'єднання? 3. Що є перетинанням графів, яка різниця цієї операції зі звичайним множинним… 4. Які властивості у перетинання?

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.199-201. 3. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по… Додаткова

Вступ

Лекція має за мету навести чисельні характеристики графів та способи представлення графів у пам’яті ЕОМ. Розглянути ступені та півступені вершин, цикломатичне та хроматичне числа, числа і множини внутрішньої та зовнішньої стійкості. Звернено увагу до ефективних способів представлення графів у пам’яті ЕОМ.

У лекції присутні два підрозділи:

17.1. Чисельні характеристики графів

17.2. Представлення графів у пам'яті ЕОМ

Чисельні характеристики графів

Розв’язання багатьох задач методами теорії графів зводиться до визначення тих чи інших чисельних характеристик графів.

Ступінь вершин

Для орієнтованого графу G = <X, Г> число дуг, що входять у вершину називається напівступенем заходу р(хі) " xi (p(xi) ³ |Г-1 (xi)|); число дуг, що виходять з вершини xi - напівступенем виходу s(xi)

Цикломатичне число

Визначення. Цикломатичним числом графу називається число n, що дорівнює n(G) = m –n + r Цикломатичне число має цікавий фізичний зміст - воно дорівнює найбільшому числу незалежних циклів у графі. При…

Хроматичне число

Визначення. Граф називається р-хроматичним, якщо його вершини можна розфарбувати “р” різними кольорами так, щоб ніякі дві суміжні вершини не були… Визначення. Найменше число р, при якому граф є р-хроматичним, називається… Якщо ¡(G) = 2, то граф називається біхроматичним. Необхідною і достатньою умовою біхроматичності графу є…

Множина внутрішньої стійкості

" xi ÎS (Г(xi)ÇS = Æ) Множина внутрішньої стійкості, що містить найбільше число елементів, є… Приклад. Два графи з різними числами внутрішньої стійкості

Множина зовнішньої стійкості

" xi Ï T (Г(xi)ÇT ¹ Æ) Множина зовнішньої стійкості, що містить мінімальне число елементів, зветься… Приклад. Однакові числа зовнішньої стійкості для різних графів, що включають п'ять вершин, відповідно рівні 2, 2

Представлення графів у пам'яті ЕОМ

Недоліком способу є велика порожнина матриці, непродуктивне використання пам'яті для графів з малою кількістю ребер, а також великий час обробки… Другий вид представлення графів - за допомогою матриці інцидентності -… Третій вид представлення графів - за допомогою списків суміжності - використовується найчастіше, поряд з використанням…

Контрольні запитання

2. Як визначається цикломатичне число? 3. Якій граф є p-хроматичним, біхроматичним? 4. Що є хроматичним числом графу?

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.201-206. 3. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по… Додаткова

Вступ

Лекція має за мету навести основні поняття і визначення теорії скінченних автоматів. Розглянуто автомати Мілі та Мура як п'ятірка об'єктів, зміни станів на вході, усередині, на виході у дискретному часі, відображення вхідних слів у вихідні, способи завдання автоматів, розширення функцій. Звернено увагу до поведінки автоматів у часі.

У лекції присутні три підрозділи:

18.1. Абстрактний автомат

18.2. Способи завдання автоматів

18.3. Розширення функцій d і l

Абстрактний автомат

Поводження будь-якого ДУ визначається зміною його вхідних і вихідних символів і внутрішніх станів. Особливістю функціонування ДУ є те, що в часі… Визначення. Абстрактний автомат працює в дискретному часі. Абстрактний автомат… A = (X, Y, S, d, l, {s0})

Способи завдання автоматів

Для завдання кінцевого автомата А необхідно задати усі компоненти вектора А = (S, X, Y, d, l, {s₀}), тобто вхідний Х, внутрішній S і вихідний Y алфавіти, а також функції переходів і виходів. Частіше для завдання автоматів використовуються табличний і графічний способи.

Табличний спосіб

Приклад. Функція переходів автомата Мілі d:S´X®S. Таблиця 18.1 X S s1 s2 s3 …

Графічний спосіб

Дві вершини графу si і sr з'єднуються дугою, спрямованою від si до sr якщо в автоматі мається перехід з si у sr, тобто для деякого вхідного символу… При описі автомата Мура вихідний сигнал записується усередині відповідної… Приклад. Автомат Мілі з трьома станами і шістьма переходами.

Розширення функцій d і l

Для скрізь визначеного автомата функції d, d~ завжди визначені. Для часткового автомата d, d~ не визначені, якщо під дією вхідного слова автомат… Функцією заключного виходу називається функція l~(si, p), що визначає значення… Реакцією l(si, p) автомата в стані si на вхідне слово p називається вихідне слово g автомата, що з'являється на виході…

Контрольні запитання

2. Яка різниця між скрізь визначеним і частковим автоматом? 3. Що є скінченним та нескінченним автоматом? 4. Яка різниця між автоматами Мілі та Мура?

Основна

18.2. Брауэр В. Введение в теорию конечных автоматов. – М.: Радио и связь, 1987. - С.33-41, 74-82, 118-132. 18.3. Кук Л., Бейз Г. Компьютерная математика. – М.:Наука, 1990.-С.302-335. … Додаткова

Вступ

Лекція має за мету навести поняття синхронних і асинхронних автоматів Мілі і Мура. Розглянути стійки стани автомата Мура, стійки стани та виходи автомата Мілі, що дозволяють ввести синхронні та асинхронні автомати. Звернено увагу до перетворення автоматів Мілі та Мура, а також до моделі С-автомата.

У лекції присутні чотири підрозділи:

19.1. Синхронні й асинхронні автомати

19.2. Асинхронні автомати, що тактуються

19.3. Перетворення автоматів Мілі і Мура

19.4. Сполучена модель автоматів – С-автомат

Синхронні й асинхронні автомати

Автомат Мура називається асинхронним, якщо кожен його стан si Î S – стійкий. У противному випадку А – синхронний. Приклад : Асинхронний автомат Мура. Таблиця 19.1 S X Y s1 y1 s2 y3 s3 y2 x1 s2 s2 …

Асинхронні автомати, що тактуються

a) вхідний алфавіт Х автомата А розбивається на дві підмножини X’={х'1, х'2,…x’m} і X’’={х'’1, х'’2,…x’’e}; b) при подачі на А якої-небудь букви х'j Î Х’ існує не менш одного переходу автомата А в будь-якій стан;

Перетворення автоматів Мілі і Мура

Для будь-якого автомата Мура можна побудувати еквівалентний йому автомат Мілі і навпаки.

Перетворення автомата Мура в автомат Мілі

Нехай заданий автомат Мура АA = (SA, XA, YA, dA, lA, {s0A}), еквівалентний йому автомат Мілі АB = (SB, XB, YB, dB, lB, {s0B}) будується в такий… SB : = SA, XB : = XA,

Перетворення автомата Мілі в автомат Мура

XВ := XА; YВ := YА. Для визначення SВ кожному стану siÎ SА ставиться у відповідність множина… Число елементів множини Sів дорівнює множині різних вихідних сигналів на дугах автомата А, що входять у стан sіа.…

Сполучена модель автоматів – С-автомат

С = (S, X, Y, U, d, l1, l2, {s0 }), де S – множина внутрішніх станів, Х – вхідний алфавіт, Y – вихідний алфавіт… Сполучений С-автомат представляється у вигляді пристрою з одним входом і двома виходами (рис. 19.7.).

Контрольні запитання

2. Якій автомат Мура є синхронним, а якій асинхронним? 3. Що є стійким виходом автомата Мілі? 4. Якій автомат Мілі є синхронним, а якій асинхронним?

Основна

2. Мелихов А.Н. Ориентированные графы и конечные автоматы. – М.: Наука, 1971. – С.154-182. 3. Кук Л., Бейз Г. Компьютерная математика. – М: Наука, 1990. - С.302-335. Додаткова

Вступ

Лекція має за мету навести основні поняття композиції автоматів Мілі і Мура. Розглянути рівнобіжне з'єднання автоматів, послідовне з'єднання двох автоматів, з'єднання зі зворотним зв'язком, з'єднання автоматів з вихідною функцією. Звернено увагу до визначення функцій переходів і вихідів результуючого автомата, а також на узгодження часу у автоматах композиції.

У лекції присутні два підрозділи:

20.1. Композиція автоматів

20.2. З'єднання автоматів з вихідною функцією

Композиція автоматів

При композиції автоматів використовуються основні з'єднання: рівнобіжне; послідовне; зі зворотним зв'язком.

Рівнобіжне з'єднання

  Рис. 20.1. Рівнобіжне з'єднання автоматів

Послідовне з'єднання двох автоматів

  Рис. 20.2. Послідовне з'єднання автоматів

З'єднання зі зворотним зв'язком

У випадку з'єднання зі зворотним зв'язком принаймні один з автоматів A1 чи A2 повинен бути автоматом Мура, інакше стабільність системи не…  

З'єднання автоматів з вихідною функцією

Нехай tз1 – затримка, що внесена dі, lі-функціями, тобто затримка спрацьовування деякого автомата Ai, тоді сигнал на виході A3 з'явиться не раніш,…  

Контрольні запитання

2. Що є початковим станом і як визначаються функції переходів та виходів рівнобіжного з’єднання автоматів? 3. Яке з’єднання автоматів є послідовним? 4. Як визначаються функції переходів та виходів послідовного з’єднання автоматів?

Основна

2. Брауэр В. Введение в теорию конечных автоматов. – М.: Радио и связь, 1987. - С.33-41, 74-82, 118-132. 3. Кук Л., Бейз Г. Компьютерная математика. – М: Наука, 1990. - С.302-335. Додаткова

Вступ

Лекція має за мету навести основні поняття загальної мережі автоматів. Розглянуто визначення мережі та компонентного автомату, еквівалентних автоматів для мережі автоматів. Звернено увагу до визначення функцій еквівалентних автоматів.

У лекції присутні два підрозділи:

21.1. Мережі автоматів

21.2. Еквівалентні автомати мережі

Мережі автоматів

Визначення. Мережа автоматів – це шістка N = (X, {Ai}, Y, {fi’}, {fi”}, g), де X иY – відповідно вхідний і вихідний алфавіти мережі Ni; {Ai} -… Компонентні автомати {Ai} утворюють базис мережі, а множина функцій {fi},… Ai = (Si, Xi d і,{s0і}).

Еквівалентні автомати мережі

  Рис. 21.2. Мережа з n компонентних автоматів

Контрольні запитання

1. Що є мережею автоматів, що узагальнює мережа автоматів?

2. Що є компонентним автоматом?

3. Яка різниця між компонентним автоматом та звичайним напівавтоматом?

4. Що є еквівалентним автоматом для мережі автоматів?

5. Як визначити функції переходів та вихідів для еквівалентного автомата мережі автоматів?

Список літератури

Основна

21.2. Брауэр В. Введение в теорию конечных автоматов. – М.: Радио и связь, 1987. - С.33-41; 74-82; 118-132. 21.3. Кук Л., Бейз Г. Компьютерная математика. – М: Наука, 1990. -С.302-335. … Додаткова

Вступ

Лекція має за мету навести базові поняття булевих функцій. Розглянути логічні, однорідні функції, тривіальні булеві функції від одного та двох аргументів. Звернено увагу на булеві формули, що будуються за допомогою суперпозиції, а також на рівнопотужність формул.

У лекції присутні три підрозділи:

22.6. Логічні функції

22.7. Булеві функції

22.8. Логічні формули

22.1. Логічні функції

Відмінна риса логічних функцій полягає в тому, що вони приймають значення в скінченних множинах, тобто область значень логічної функції - завжди кінцева множина.

Якщо область значень логічної функції містить k різних елементів, то функція називається k-значною.

Логічні функції можуть залежати від однієї, двох і більше числа змінних (аргументів) x₁, x₂,..., x_n, що на відміну від самої функції можуть приймати значення елементів як скінченних, так і нескінченних множин. У теоретико-множинному змісті логічна функція від ²n² змінних y=f(x₁, x₂,..., x_n) являє собою відображення множини наборів слів (n-мірних кортежів, векторів) вигляду <x₁, x₂,..., x_n>, що є областю її визначення, на множину її значень U={y₁, y₂,..., y_k}.

Якщо аргументи приймають значення з тієї ж множині, що і сама функція, то її називають однорідною.

22.2. Булеві функції

Найбільш простим і найбільш важливим класом однорідних логічних функцій є клас двозначних булевих функцій.

Визначення. Булевою функцією називається однорідна логічна функція, що приймає значення з двоелементної булевої множини В={0, 1}, або В={кривда, істина}.

Тому що булева функція - однорідна, то будь-Якій її аргумент приймає значення з В={0, 1} чи В={хибність, істина}, область визначення булевої функції від ²n² змінних (аргументів) - це множина слів довжини ²n². Загальне число всіляких двійкових наборів довжини ²n² дорівнює 2ⁿ . Число всіляких булевих функцій від ²n² аргументів дорівнює 2^{2^n} (2^n – це два у степені n) . Будь-яка булева функція може бути задана таблицею істинності (відповідності), у лівій частині якої перераховані всі 2ⁿ наборів значень змінних, а в правій частині - значення функції на цих наборах.

Приклад. а) n=3, число наборів - 2³=8, число функцій - 2^{2^n}= 2⁸=256;

б) n=5, число наборів - 2⁵= 32, число функцій - 2³²- >4×10⁹.

Булеві функції від однієї і двох змінних докладно досліджені.

Булеві функції однієї змінної

n=1, число наборів - 2¹=2, число функцій - 2²=4

Таблиця 22.1

х	Y0	Y1	Y2	Y3

 

Y₀ і Y₃ - функції-константи (Y₀ - константа ²0², Y₃ - константа ²1²), що приймають постійні значення на всіх наборах аргументів. Функція U₁ повторює значення аргументу. Функції U₀, U₁, U₃ - тривіальні функції. Єдина нетривіальна функція - U₂, називається запереченням, чи інверсією, тобто y₂=`x і читається як ²у₂ дорівнює не x².

Булеві функції двох змінних

n=2, число наборів 2²=4, число функцій - 2⁴=16

Таблиця 22.2

Х1х2

у0 0

у1 Ù

у2 ù®

у3 х1

у4 ù¬

у5 х2

y6 Å

у7 Ú

y8 ¯

у9 ~

у10 ùх2

у11 ¬

у12 ùх1

у13 ®

у14 /

У15 1

 

З наведених функцій шість функцій не залежать від х₁, чи х₂, чи обох разом. Це у₀=0 - константа нуля, у₁₅=1 - константа одиниці, функції повторення у₃=х₁ і у₅=х₂, а також функції заперечення у₁₀=`х<sub>2</sub> і у<sub>12</sub>=`х₁. Інші булеві функції залежать від двох змінних. Частина з них має свої специфічні назви і широко використовуються в булевої алгебрі.

1. Булева функція кон’юнкції (логічного множення)

у₁=х₁Ùх₂, чи у₁=х₁&х₂, чи у=х₁×х₂, чи у=х₁х₂, чи у=х₁ і х₂.

Дану функцію називають логічним множенням, тому що її таблиця істинності збігається з таблицею множення для чисел ²0² і ²1², тобто дорівнює одиниці тільки при одиничних аргументах.

 

2. Булева функція диз'юнкції (логічного додавання)

у₇=х₁Úх₂, чи у₇=х₁+х₂, чи у₇=х₁, чи х₂

Дана функція дорівнює одиниці, якщо хоча б один з аргументів дорівнює одиниці.

3. Булева функція додавання за модулем (нерівнозначності)

у₆ =х₁Å х₂, чи у₆=(`х<sub>1</sub> і х<sub>2</sub>), чи (х<sub>1</sub> і `х₂)

Дана функція дорівнює одиниці на незбіжних наборах х₁ і х₂.

4. Булева функція еквівалентності (рівнозначності)

у₉ =х₁~х₂, чи у₉=х₁ºх₂, чи у₉=(`х<sub>1</sub> і `х₂),чи (х₂ і х₁).

Дана функція дорівнює одиниці на збіжних наборах х₁ і х₂.

5. Булева функція імплікації (логічного проходження)

у₁₃=х₁®х₂ читається, «якщо х₁, то х₂ », чи у₁₃= `х₁, чи х₂.

Дана функція дорівнює одиниці при х₁, дорівнюючому нулю і функція повторює значення х₂ при х₁, дорівнюючому одиниці, у₁₁=х₂®х₁, читається «якщо х₂, то х₁» .

6.Булева функція заперечення (заборони) імплікації

у₂=(х₁¬х₂), чи у₂=х₁ і`х₂.

В іншій інтерпретації цієї функції у₂=ù(х₁®х₂), при цьому ліва і права стрілки розуміються однаково, тобто х₁¬х₂ = x₂®x₁.

Дана функція дорівнює одиниці тільки при х₁ дорівнюючому 1 і х₂ дорівнюючому 0. Аналогічно, у₄=х₂¬х₁ у першій інтерпретації дорівнює одиниці тільки при х₂ дорівнюючому 1 і x₁ дорівнюючому 0.

7. Булева функція «стрілка Пірса» (заперечення диз'юнкції)

у₈=х₁¯х₂, чи у₈= `х<sub>1</sub> і `х₂.

Дана функція приймає одиничне значення тільки при нульових значеннях х₁ і х₂. У цьому зв'язку у₈ є запереченням диз'юнкції, у₈ =`у₇ .

8. Булева функція «штрих Шеффера» (заперечення кон'юнкції)

у₁₄=х₁/х₂ чи у₁₄= `х<sub>1</sub> чи `х₂.

Дана функція приймає одиничне значення, якщо хоча б х₁ чи х₂ дорівнює нулю. У цьому зв'язку у₁₄ є запереченням кон'юнкції, у₁₄=`у₁.

22.3. Логічні формули

Часто використовуваними є булеві функції заперечення у=`х (унарна), кон'юнкції у=х₁Ùх₂ (бінарна), диз'юнкції у=х₁Úх₂ (бінарна).

Вираження, за допомогою яких задаються булеві функції, називаються логічними формулами - булевими змінними, зв'язаними знаками логічних операцій. Складні формули виводять суперпозицією (заміщенням, підстановкою) вхідних у них змінних іншими формулами.

Приклад. Нехай у=х₁Úх₂, де х₁=`а, х<sub>2</sub>=b×c, тоді в результаті суперпозиції у =`аÚb×c

Кожна формула визначає деяку булеву функцію. Її значення при різних значеннях змінних можна визначити на підставі таблиці істинності для функцій двох змінних.

Приклад. а=0, b=0, c=1, х₁=`а=`0=1; х₂=b×c=0×1=0; у=х₁Úх₂=1Ú0=1

Дві булеві функції, як і формули, називаються рівносильними, якщо при будь-яких значеннях аргументів обидві функції приймають однакові значення. Рівносильні функції з'єднують знаком рівності.

Контрольні запитання

2. Яка функція є k-значною? 3. Що таке однорідна функція? 4. Що називається булевою функцією?

Основна

2. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.504-522. 3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. -… Додаткова

Вступ

Лекція має за мету навести способи завдання булевих функцій. Розглянути табличний, аналітичний, графічний та чисельний способи, Звернено увагу до обмежень кожного зі способів. На завершення розглянуто приведення формул булевої алгебри до досконалої форми.

У лекції присутні два підрозділи:

23.1. Способи завдання булевих функцій

23.2. Приведення формул булевої алгебри до досконалої форми

23.1. Способи завдання булевих функцій

Існують чотири способи завдання булевих функцій: табличний, аналітичний, геометричний і чисельний.

23.1.1. Табличний спосіб

Спосіб припускає наявність таблиці істинності (відповідності).

Приклад. Таблиця істинності функції від 3-х змінних y=f(x1, x2, x3)).

Таблиця 23.1

x1	x2	x3	Y

 

23.1.2. Аналітичний спосіб

Нормальні форми

Визначення. Кон'юнктивна нормальна форма (КНФ) - це кон'юнкція кінцевого числа різних членів, кожний з Якій являє собою диз'юнкцію кінцевого числа… Приклад. у=(х1`х2)Ú(х2х3`х4) ДНФ,… Визначення. Члени ДНФ, що являють собою елементарні кон'юнкції з ²k² букв, називаються мінтермами к-го…

Контрольні запитання

2. Що таке ДНФ і КНФ, СДНФ і СКНФ? 3. Яка різниця між мінтермом і макстермом? 4. Що є “констітуентою одиниці” і “конституентою нуля”?

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.88-91. 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Вступ

Лекція має за мету навести основні поняття булевої алгебри. Розглянути шістнадцять властивостей операцій булевого базису {Ù, Ú, ù}, спрощення запису формул, подвійність формул булевої алгебри, подвійні і самоподвійні функції. Звернено увагу до булевої алгебри множин і булевої алгебри двійкових векторів, уведено поняття ізоморфних алгебр.

У лекції присутні чотири підрозділи:

24.1. Булева алгебра

24.2. Спрощення запису формул

24.3. Подвійність формул булевої алгебри

24.4. Булева алгебра множин

24.1. Булева алгебра

Нехай задана деяка множина М и набір операцій Ф, що виконуються на цій множини Ф = {j₁, j₂,..., j_n}, тоді двійка множин А = (М, Ф) називається алгеброю. Множина М називається основною, чи несучою множиною. Множина Ф називається сигнатурою операцій, чи просто сигнатурою.

Визначення. Булевою алгеброю В = (М, {Ú, Ù, ù} 0, 1) називається множина М с двома бінарними операціями “Ú” і “Ù”, однією унарною операцією інверсії “ù” у сигнатурі і двома відзначеними елементами (універсальними границями) “0” і “1”, причому для будь-яких x₁, x₂, x₃, що належать множині M, набір операцій відповідає наступним тотожностям.

Основні тотожності булевої алгебри

1. x₁Ùx₂=x₂Ùx₁; x₁Úx₂=x₂Úx₁;
комутативність

2. x₁Ù(x₂Ùx₃)=(x₁Ùx₂)Ùx₃; x₁Ú(x₂Úx₃)=(x₁Úx₂)Úx₃;
асоціативність

3. x₁Ù(x₂Úx₃)=(x₁Ùx₂)Ú(x₁Ùx₃); x₁Ú(x₂Ùx₃)=(x₁Úx₂)Ù(x₁Úx₃);
дистрибутивність;

4. x₁Ù0=0; x₁Ú0=x₁;
x₁Ù1=x₁; x₁Ú1=1;
`0=1; `1=0;

універсальні границі;

5. x₁Ùx₁=x₁; x₁Úx₁=x₁;
ідемпотентність;

6. x₁Ù`x<sub>1</sub>=0; x<sub>1</sub>Ú`x₁=1;
ù(`x)=x;
доповнення і інволютивність

7. x₁Ù(x₁Úx₂)=x₁; x₁Ú(x₁Ùx₂)=x₁;
поглинання;

8. (x₁Ùx₂)Ú(x₁Ù`x<sub>2</sub>)=x<sub>1</sub>; (x<sub>1</sub>Ùx<sub>2</sub>)Ú(x<sub>1</sub>Ù`x₂)=x₁;
Блейка-Порецького;

9. x₁Ù(`x<sub>1</sub>Úx<sub>2</sub>)=x<sub>1</sub>Ùx<sub>2</sub>; x<sub>1</sub>Ú(`x₁Ùx₂)=x₁Úx₂;
(x₁Ùx₃)Ú(x₂Ù`x<sub>3</sub>)= (x<sub>1</sub>Úx<sub>3</sub>)Ù(x<sub>2</sub>Ú`x₃)=
=(x₁Ùx₃)Ú(x₂Ù`x<sub>3</sub>)Ú(x<sub>1</sub>Ùx<sub>2</sub>); =(x<sub>1</sub>Úx<sub>3</sub>)Ù(x<sub>2</sub>Ú`x₃)Ù(x₁Úx₂);

склеювання;

10. ù(x₁Ùx₂)=`x<sub>1</sub>Ú`x₂; ù(x₁Úx₂)=`x<sub>1</sub>Ù`x₂;
де Моргана

Крім десяти основних тотожностей необхідно визначити теореми підстановки (11-14) і теореми розкладання (15, 16), що можуть скоріше привести до мінімальної формули.

11. x_i×f(x₁, x₂,..., x_i,`x_i,..., x_n)=x_i×f(x₁, x₂,..., 1, 0,..., x_n);

12. `x<sub>i</sub>×f(x<sub>1</sub>, x<sub>2</sub>,..., x<sub>i</sub>,`x_i,..., x_n)=`x_i×f(x₁, x₂,..., 0, 1,..., x_n);

13. x_iÚf(x₁, x₂,..., x_i,`x_i,..., x_n)=x_iÚf(x₁, x₂,..., 0, 1,..., x_n);

14. `x<sub>i</sub>Úf(x<sub>1</sub>, x<sub>2</sub>,..., x<sub>i</sub>,`x_i,..., x_n)=`x_iÚf(x₁, x₂,..., 1, 0,..., x_n)

15. f(x₁, x₂,…, x_i,…, x_n)=(x_i×f(x₁, x₂,…,1,…, x_n))Ú(`x_i f(x₁, x₂,…, 0,…, x_n));

16. f(x₁, x₂,…, x_i,…, x_n)=(x_iÚf(x₁, x₂,…, 0,…, x_n))×(`x_iÚf(x₁, x₂,…, 1,…, x_n))

Для доказу тотожностей можна використовувати метод зіставлення таблиць істинності лівої і правої частини тотожностей – досить переконатися в однакових значеннях на відповідних наборах аргументів.

Інший метод заснований на еквівалентних перетвореннях з використанням доведених раніше тотожностей булевої алгебри.

Приклад. а) идемпотентність (збереження ступеня):

хÚх=(хÚх)×1=(хÚх)(хÚ`х)=хÚ(х×`х)=хÚ0=х;

б) поглинання:

хÚх×у=(х×1)Ú(х×у)=х×(1Úy)=x 1=х

в) Блейка-Порецького:

хÚ`х×у=(хÚ`х)×(хÚу)=1×(хÚy)=хÚy

24.2. Спрощення запису формул

З таблиці булевих функцій від двох змінних можна побачити, що між функціями є залежність у_і=`y_15-i , де 0 £ і £ 15. На підставі цього можна записати співвідношення

для констант:
0=`1 і 1=`0;

для БФ від однієї змінної:
х= ù(`х);

для БФ від двох змінних:
х₁×х₂=ù(х₁/х₂);
х₁¬х₂=ù(`х<sub>1</sub>+х<sub>2</sub>);
х<sub>1</sub>Åх<sub>2</sub>=ù(х<sub>1</sub>~х<sub>2</sub>);
х<sub>1</sub>Úх<sub>2</sub>=ù(х<sub>1</sub>¯х<sub>2</sub>);
`х₁¬х₂=ù(х₁+х₂);
х₁®`х<sub>2</sub>=`х₁+`х<sub>2</sub>);
`х₁+х₂=ù(х₁¬х₂);
х₁~х₂=ù(х₁Åх₂);
х₁¯х₂=ù(х₁Úх₂);
х₁+х₂=ù(`х₁¬х₂).

З наведених залежностей випливає, що будь-яка функція двох змінних, включаючи і константи, виражається в аналітичному вигляді через сукупність із шести функцій, що містить заперечення і будь-які функції із зазначених пар {у₀, у₁₅}, {y₁, y₁₄}, {y₂, y₁₃}, {y₄, y₁₁}, {y₆, y₉},
{y₇, y₈} і що є надлишковою.

Легко довести, що

ù(х₁®х₂)=х₁`х₂;

ù(х₁~х₂)=(х₁Ú`х<sub>2</sub>)(`х₁Úх₂) .

Сукупність можна скоротити до чотирьох функцій: “константи 0”, заперечення ²`х², диз'юнкції ²x₁Úx₂² і кон’юнкції ²х₁×х₂². Ці чотири функції також можуть бути скорочені – із законів де-Моргана і інволютивності (подвійного заперечення).

Таким чином, виконуються тотожності:

х₁Úх₂=ù(`х<sub>1</sub>×`х₂);

х₁×`х₁=0;

ù(х₁Ú`х₁)=0;

Х1×х2=ù(`х1Ú`х2).

Якщо в булевій формулі змінні зв'язані тільки одним типом операції (диз'юнкції чи кон'юнкції), то дужки не ставляться. Приклад.… Дужки, у яких береться загальна операція інверсії (заперечення), можна також опускати, тому що для операцій…

Контрольні запитання

2. Які десять основних тотожностей існують? 3. Які шість теорем розкладення і підстановки існують? 4. Як доказати тотожність булевих формул на підставі таблиць істинності?

Основна

24.2. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. - С.10-19. 24.3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Вступ

Лекція має за мету навести основні поняття алгебри Жегалкіна, функціональної повноти. Розглянути вісім властивостей операцій базису {Å, Ù}, п’ять типів булевих функцій, функціональна замкненість та повнота, критерій Поста. Звернено увагу до канонічної задачі синтезу логічних схем.

У лекції присутні п’ять підрозділів:

25.1. Алгебра Жегалкіна

25.2. Типи булевих функцій

25.3. Функціональна повнота

25.4. Логічні (перемикальні) схеми

25.5. Канонічна задача синтезу логічних схем

25.1. Алгебра Жегалкіна

Алгебра Жегалкіна задана на всій множини булевих функцій на основі двох операції: нерівнозначності Å і кон'юнкції Ù.

Визначення. Алгебра Жегалкіна – цє система А=(В, {Å, Ù}, 1), де основна множина В – цє множина усіх булевих функцій, сигнатура алгебри – {Å, Ù}, додатково алгебру поповнює константа одиниці.

Тип алгебри Жегалкіна - (2, 2), тобто вона не є булевої алгеброю.

В алгебрі Жегалкіна виконуються такі тотожності:

1. хÅу=уÅх; хÙу=уÙх
комутативність.

2. хÅ(уÅz)=(xÅy)Åz; xÙ(yÙz)=(xÙy)Ùz
асоціативність.

3. xÙ(yÅz)=(xÙy)Å(xÙz)
дистрибутивність кон'юнкції.

4. xÅ0=x; xÙ0=0;
xÅ1=`x; xÙ1=x
властивості границь.

5. хÅх=0; хÙх=х
приведення і ідемпотентність.

6. xÅ`x=1; xÙ`x=0
доповнення.

7. xÅ(xÙy)=xÙ`y; xÙ(xÅy)=xÅ(xÙy)
поглинання.

8. xÅ(`yÙz)=хÅу; xÙ(`xÅy)=хÙу
Блейка-Порецького.

9. (xÅy)Ù(xÅ`y)=0; (xÙy)Å(xÙ`y)=x
склеювання.

10. ù(xÅy)=`xÅy=xÅ`y; ù(xÙy)=(xÙy)Å1
де Моргана.

11. xÅy=(xÙ`y)Ú(`xÙy); xÅy=(xÚy)Ù(`xÚ`y)
переклад у булев базис.

12. xÅy=`xÅ`y.

13. xÚy=xÅyÅ(xÙy)
переклад у базис Жегалкіна;

14. xÅy=0Ûx=y.

15. xÅy=zÞxÅz=y або zÅy=x.

Тотожності 4, 6, 13 дозволяють перейти від будь-якої формули булевої алгебри до відповідної їй формули алгебри Жегалкіна, а за допомогою тотожностей 4, 6, 11 можна здійснити зворотний перехід від алгебри Жегалкіна до булевої алгебри.

Приклад. xÙ(`xÚy) = xÙ((1Åx)Úy) = xÙ((1Åx)ÅyÅ(1Åx)Ùy))= xÙ(1Å ÅxÅyÅyÅ(xÙy)) = xÅ(xÙx)Å(xÙyÙx) = xÅxÅ(xÙy) = xy;

1ÅxÅy=`xÅy=(xy)Ú(`x`y).

Система операцій алгебри Жегалкіна {Å, Ù} разом з константою «1» утворює так звану послаблено функціонально повну систему.

25.2. Типи булевих функцій

Визначення. У булевої алгебрі з множини булевих функцій від ²n² змінних f(x₁, x₂,..., x_n) потужності 2^{2^n} виділяються п'ять типів булевих функцій (п’ять класів попередньо повних функцій):

1. Функції, що зберігають константу «0», тобто функції, що на нульових наборах аргументів приймають нульові значення:

f(x₁, x₂,..., x_n)Þf(0, 0,..., 0)=0.

Приклад. f(x₁, x₂)=x₁Ùx₂Þf(0, 0)=0.

2. Функції, що зберігають константу «1», тобто функції, що на одиничних наборах аргументів приймають одиничні значення:

f(x₁, x₂,..., x_n)Þf(1, 1,..., 1)=1.

Приклад. f(x₁, x₂)=x₁Ùx₂Þ f(1, 1)=1.

3. Самоподвійні функції, що приймають протилежні значення на будь-яких двох протилежних наборах:

Приклад. f(x)=`xÞf(0)=1, f(1)=0.

4. Лінійні функції, що являються в алгебрі Жегалкіна канонічним багаточленом, що не утримує добутків змінних:

f(x₁, x₂,..., x_n)=a₀Å a₁×x₁Åa₂×x₂Å...Åa_n×x_n,

де а₀, а₁, а₂,..., а_n – константи, що приймають значення 0 чи 1

Приклад. f(x)=1Å x₁Å x₂.

5. Монотонні функції, що для будь-яких двох упорядкованих наборів аргументів <x₁₁, x₁₂,..., x_1n> і <x₂₁, x₂₂,..., x_2n>, де <x₁₁, x₁₂,..., x_1n> £ £<x₂₁, x₂₂,.., x_2n>, приймають також упорядковані значення, тобто f(x₁₁, x₁₂,..., x_1n)£ f(x₂₁, x₂₂,..., x_2n).

Приклад. f₁(x₁, x₂)=x₁Úx₂, f₂(x₁, x₂)=x₁Ùx₂, f₃(x₁, x₂)=x₂

<x₁, x₂> f₁: f₂: f₃:

<0, 0> 0 0 0

<0, 1> 1 0 1

<1, 0> 1 0 0

<1, 1> 1 1 1

Крім ціх п’яти типів, викреслюють тип сіметричних функцій.

Визначення. Булева функція симетрична по змінним x_i, x_j, якщо
f(…, x_i,…,x_j,…) = f(…, x_j,…,x_i,…). Булева функція симетрична, якщо вона симетрична по усім парам змінних.

Приклад. Функція f = x₁`x<sub>2</sub>`x₃ Ú `x<sub>1</sub>`x₂x₃ симетрична по змінних x₁ і x₃. Функція f = x₁x₂ Ú x₁x₃ Ú x₂x₃ симетрична.

25.3. Функціональна повнота

Визначення. Система булевих функцій називається функціонально повною, якщо суперпозиція цих функцій дозволяє одержати будь-яку функцію з множини булевих функцій.

Приклад. Система функцій {Ú, Ù, ù } є функціонально повною, але система функцій {Å, Ù} не функціонально повна.

Якщо у функціонально повній системі є функції константи «0» чи константи «1», то вона послаблено функціонально повна. Функціонально повна система функцій утворює базис у логічному просторі.

Приклад. Система функцій {Å, Ù}, що поповнена константою одиниці, тобто {{Å, Ù} 1}, послаблено функціонально повна.

Визначення. Система булевих функцій називається мінімально повним базисом, якщо видалення з неї будь-якої функції перетворює цю систему в неповну.

Приклад. Мінімально повний базис є {Ù, ù }, але система {Ú, Ù, ù } не є мінімально повним базисом.

Визначення. Усяка сукупність функцій алгебри логіки, замкнута щодо суперпозиції, тобто така, що будь-яка суперпозиція функцій із сукупності знову породжує функцію, що належить ції же сукупності, називається функціонально замкнутим класом.

Функціонально замкнуті класи, відмінні від порожнього класу і сукупності всіх можливих булевих функцій, називаються власними функціонально замкнутими класами. Власний функціонально замкнутий клас називається передповним, якщо він не міститься ні в якому функціонально замкнутому класі, що є відмінним від даного класу і класу всіх можливих булевих функцій.

Приклад. Система функцій, що зберегають одиницю, є функціонально замкнутим класом, система функцій, що монотонно убивають, не є функціонально замкнутим класом. Перша система є поперед повною.

Теорема про функціональну повноту (критерій Поста): Для того, щоб система булевих функцій була повною, необхідно і досить, щоб вона включала хоча б одну функцію, що не зберігає константу «0», хоча б одну функцію, що не зберігає константу «1», хоча б одну функцію, що несамоподвійна, хоча б одну функцію, що нелінійна, і хоча б одну функцію, що немонотонна.

Та сама функція може представляти у функціонально повній системі одне чи кілька необхідних властивостей, якщо вона має ці властивості.

Приклад. Властивості елементарних булевих функцій.

Таблиця 25.1.

Булева функція	Фор-мула	Незбер. ”0”	Незбер. ”1”	Несамо-двоїста	Нелі-нійна	Немо-нотонна
Константа “0”	0		+	+
Константа “1”	1	+		+
Заперечення	ù x	+	+			+
Кон'юнкція	x1Ùx2			+	+
Диз'юнкція	x1Úx2			+	+
Сума за модулем “2”	x1Åx2		+	+		+
Штрих Шеффера	x1/x2	+	+	+	+	+
Стрілка Пірса	x1¯x2	+	+	+	+	+

З таблиці видно, що системи функцій {кон'юнкція, заперечення}, {диз'юнкція, заперечення}, {штрих Шеффера}, {стрілка Пірса} задовольняють теоремі Поста. Система функцій {Ú, Ù, ù} утворює так званий булевий базис.

25.4. Логічні (перемикальні) схеми

Для реалізації булевих функцій розробляються і використовуються релейні і логічні елементи, що є звичайно напівпровідниковими приладами, що виконані за субмікронною технологією. Їхні входи відповідають булевим змінним, виходи - реалізованої функції. Для позначення логічних елементів використовують прямокутники, трикутники, або інші фігури. У полі фігури елемента може бути указана та операція, що він реалізує. Подібно суперпозиції булевих функцій логічні схеми будують з'єднанням логічних елементів.

Приклад. Релейні (контактні) схеми).

 

Рис. 25.1. Релейні перемикальні схеми для трьох функцій
а - y₁ =`x; б - y<sub>2</sub> = x; с - у<sub>3</sub> =`x₁Ú(x₂×`x₃)

 

Приклад. Логічна схема з п’яти елементів.

 

Рис. 25.2. Логічна схема для функції y = (x₁×`x<sub>2</sub>) Ú(`x₁× x₂)

25.5. Канонічна задача синтезу логічних схем

Пристрої, що реалізують елементарні булеві функції, називаються логічними елементами. Логічною схемою називається з'єднання (суперпозиція) логічних елементів.

Задача побудови логічної схеми, що відповідає заданій булевій функції, називається задачею синтезу.

Задача визначення булевої функції для заданої логічної схеми називається задачею аналізу.

Між формулою, що відповідає булевій функції, і логічною схемою, що реалізує формулу, існує взаємно однозначна відповідність. Однак та сама булева функція може бути представлена за допомогою декількох формул, отже, можна побудувати кілька схем, що реалізують ту саму булеву функцію. Такі логічні схеми називаються еквівалентними. Очевидно, що більш простій формулі відповідає і більш проста логічна схема. Прийнято вважати більш простою ту формулу, що містить менше число змінних і логічних операцій. Таким чином, для одержання більш простої логічної схеми необхідно провести спрощення формули логічної функції за допомогою логічних перетворень.

Визначення. Канонічна задача синтезу логічних схем у булевому базисі (Ú, Ù, ù ) зводиться до такого:

1. Вихідна булева функція представляється в СДНФ (СКНФ).

2. За допомогою операцій доповнення, поглинання булева функція приводиться до вигляду ДНФ (КНФ), що містить кількість (букв) змінних і знаків операцій, яка не піддається скороченню, тобто тупикової ДНФ (тупикової КНФ) чи ТДНФ (ТКНФ).

3. Для отриманої ТДНФ (ТКНФ) будується логічна схема.

Операції доповнення:

(x₁×x₂)Ú(x₁×`x<sub>2</sub>)=x<sub>1</sub>; (x<sub>1</sub>Úx<sub>2</sub>) (x<sub>1</sub>Ú`x₂)=x₁.

Операції поглинання:

x₁Ú(x₁×x₂)=x₁; x₁(x₁Úx₂)=x₁.

У результаті застосування операцій доповнення і поглинання виходять формули, для яких подальші операції доповнення і поглинання застосувати неможна, тобто тупикові форми - ТДНФ і ТКНФ. Серед тупикових форм знаходиться і мінімальна (МДНФ і МКНФ), причому мінімальних форм може бути кілька. Ще один крок у мінімізації – одержання форми у дужках (СкНФ).

Приклад.y=x₁x₂`x<sub>3</sub>Ú`x₁x₂x₃Úx₁x₂x₃ СДНФ

y=x₁x₂`x<sub>3</sub>Ú`x₁x₂x₃Úx₁x₂x₃Úx₁x₂x₃

y=x₁x₂Úx₂x₃ МДНФ

y=x₂(x₁Úx) СкНФіф (і МКНФ).

Контрольні запитання

2. Які вісім основних тотожностей алгебри Жегалкіна існують? 3. Як привести формулу функції з булевої алгебри в алгебру Жегалкіна та… 4. Які типи булевих функцій існують?

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.94-98. 3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. -… Додаткова

Вступ

Лекція має за мету навести два найбільш наочних метода мінімізації булевих функцій. Розглянута відповідність між мінтермами (макстермами) та елементами n-вимірного куба, а також мінтермами та клітками таблиці Карно і Закревського. Звернено увагу до кодування стовпців та рядків карт Карно і Венна, до обмежень графічного і табличного методів.

У лекції присутні два підрозділи:

26.1. Графічний метод мінімізації булевих функцій

26.2. Табличний метод мінімізації

26.1. Графічний метод мінімізації булевих функцій

Кожній вершині n-мірного куба можна поставити у відповідність константу одиниці. Отже, підмножина відзначених вершин є відображенням булевої функції від n змінних у СДНФ.

Для відображення функції від n змінних, представленої в СДНФ, необхідно установити відповідність між її мінтермами й елементами n-вимірного куба.

Мінтерм n-го рангу для функції n-змінних відповідає вершині
n-вимірного куба. Мінтерм (n-1)-го рангу можна розглядати як результат доповнення двох мінтермів n-го рангу, що відрізняються однією змінною:

Jn-1=(jn-1×xi)Ú(jn-1×`xi).

Аналогічно установлюється відповідність мінтермів (n-2)-го порядку граням n-вимірного куба, кожна з яких покриває чотири вершини або два ребра… Елементи n-вимірного куба, що характеризуються ²S² вимірами,… Приклад. Для функції від трьох змінних y= x1`x2`x3 Ú x1`x2 x3 Ú Ú`x1`x2 x3 Ú`x1 x2 x3…

Контрольні запитання

2. Що зіставляється конституенті одиниці або нуля у n-вимірному кубі? 3. Що зіставляється мінтерму або макстерму (n-k)-го рангу у n-вимірному… 4. Що є s-кубами для n-вимірного куба?

Основна

2. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… 3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. -… Додаткова

Вступ

Лекція має за мету навести базові поняття та методи аналітичної мінімізації булевих функцій. Розглянути поняття комплексів кубів, постановка задачі мінімізації, метод Квайна, таблиці покриття та алгебраїчний метод. Основну увагу звернено до дій з комплексом кубів, побудови та роботи з таблицею покриття та скороченою таблицею покриття.

У лекції присутні три підрозділи:

27.1. Аналітичні методи мінімізації

27.2. Метод Квайна

27.3. Алгебраїчний метод одержання мінімального покриття (алгоритм Петрика)

27.1. Аналітичні методи мінімізації

27.1.1. Комплекс кубів

Аналітичні методи мінімізації використовують спеціальні методи представлення булевих функцій. Деякі з цих методів використовують комплекс кубів.

Визначення. Комплекс кубів К(у) функції y=f(x₁, x₂,..., x_n) - це об'єднання множин Кs(y) усіх s-кубів, де 0£s£n-1, причому деякі з Кs(y) можуть бути порожніми:

К(у)=È Кs(y)

Кожен s-куб відображає визначений мінтерм. Для запису s-кубів і відповідних їм мінтермів функції від «n» змінних використовують слова довжини «n». Вхідні в мінтерм змінні називаються зв'язаними і являються одиницею для x_i або нулем для `хі. Не вхідні в мінтерм (відсутні) змінні називаються вільними і позначаються через «´» (хрест), або через «~» (тильда).

Приклад. n=5 `x<sub>1</sub>`x₂x₃x₄`x₅Þ 00110 - 0-куб

x₁`x₃x₄ Þ 1´01´ - 2-куб

`x<sub>1</sub>x<sub>2</sub>`x₅ Þ 01´´0 - 2-куб

x₃`x₅ Þ ´´1´0 - 3-куб

Нуль-куби (0-куби) відповідають конституентам одиниці, або конституентам нуля. Сукупність усіх s-кубів записується як множина слів у алфавіті {0, 1, ´}, або {0, 1, ~}, що відповідають кубам визначеної розмірності відповідно зв'язаним та вільним змінним.

Приклад. y = x₁`x<sub>2</sub>`x₃ Ú x₁`x<sub>2</sub>x<sub>3</sub> Ú`x₁`x<sub>2</sub>x<sub>3</sub> Ú`x₁x₂x₃ Ú`x<sub>1</sub>x<sub>2</sub>`x₃Ú x₁x₂x₃. К(y) = К°ÈК¹ÈК²,

де K° = 1 0 0 K¹ = {1 0 ´ K² = {´ ´ 1}

1 0 1 ´ 0 1

0 0 1 0 ´ 1

0 1 1 ´ 1 1

0 1 0 1 ´ 1

1 1 1} 0 1 ´}

Комплекс кубів утворює максимальне покриття функції. Крім того, виключаючи із нього всі ті S-куби, що покриваються кубами вищої розмірності, одержуємо скорочене покриття. Скорочене покриття дозволяє сполучити множину тупикових покрить. На множині тупикових покрить визначаються мінімальні.

Якщо використати куби для позначення макстермів, точно в такий же спосіб можна одержувати тупикові і мінімальні покриття для КНФ.

27.1.2. Постановка задачі

Мінімізація схем у булевому базисі зводиться до пошуку мінімальної ДНФ, якій відповідає мінімальне покриття. Для оцінки складності булевої функції використовується критерій Квайна, що формулюється таким чином:

Твердження: Мінімальній функції відповідає мінімальна ціна за Квайном, обумовлена як С=åq_s(n-s), де q_s - число S-кубів, що утворюють покриття даної функції від n змінних, s - розмірність кубів.

Мінімальне покриття характеризується мінімальною ціною.

Приклад. y=x₁`x<sub>3</sub>x<sub>4</sub>Úx<sub>1</sub>x<sub>2</sub>Ú`x₁x₃ n=4

C=1×(4-1)+2×(4-2)=3+4=7.

Задача мінімізації здійснюється в два кроки.

На першому кроці знаходиться скорочене покриття, що містить всі S-куби максимальної розмірності і не утримує жодного куба, що покривається Якім-небудь кубом цього покриття.

Відповідну скороченому покриттю ДНФ називають скороченою ДНФ, а її мінтерми - простими імплікантами. Для будь-Якій булевої функції скорочене покриття є єдиним, але воно може бути надлишковим унаслідок того, що деякі з кубів покриваються сукупностями інших кубів.

На другому кроці здійснюється перехід від скороченої ДНФ до тупикової ДНФ, утвореної зі скороченої ДНФ виключенням усіх надлишкових кубів, без яких сукупність кубів, що залишилася, ще утворить покриття даної булевої функції, але при подальшому виключенні кожного з кубів одержувана сукупність кубів вже не покриває задану функцію, тобто перестає бути покриттям.

Куб скороченого покриття, що покриває вершини даної булевої функції, які не покриваються ніЯкіми іншими кубами скороченого покриття, не може виявитися надлишковим і завжди увійде в мінімальне покриття. Такий куб, як і відповідна йому імпліканта, називається екстремаллю чи істотною імплікантою, а вершини, що покриваються ними, - відзначеними вершинами. Множина екстремалей утворює ядро покриття.

При переході від скороченого покриття до мінімального спочатку виділяється ядро покриття. Якщо множина екстремалей не утворить покриття, то воно доповнюється тим чи іншим способом до покриття кубами зі скороченого покриття. На множини отриманих таким чином тупикових покрить вибирається мінімальне.

СДНФ Þ СкДНФ Þ {ТДНФ} Þ {МДНФ}

Приклад. y =`x<sub>1</sub> x<sub>2</sub>`x₃ Ú`x<sub>1</sub> x<sub>2</sub> x<sub>3</sub> Ú x<sub>1</sub>`x₂`x<sub>3</sub> Ú x<sub>1</sub>`x₂ x₃ Ú x₁ x₂ x₃

K₀ = 0 1 0 K₁ = 0 1 ´ K₂ = Æ

0 1 1 ´ 1 1

1 0 0 1 0 ´

1 0 1 1 ´ 1

1 1 1

CкДНФ =К₁ ТДНФ₁ = 0 1 ´ ТДНФ₂ = 0 1 ´

1 0 ´ ´ 1 1

1 ´ 1 ` 1 0 ´

МДНФ₁ = 0 1 ´ МДНФ₂ = 0 1 ´

1 0 ´ ´ 1 1

1 ´ 1 1 0 ´.

27.2. Метод Квайна

Як вихідну форму булевої функції для мінімізації методом Квайна використовують СДНФ чи таблицю істинності. Приведення до скороченого ДНФ здійснюється застосуванням властивостей доповнення (операції склеювання).

Ахі)Ú (a`xi)=a

Приклад. 0-куби: 1010 Þ 1-куб: 10´0. Якщо порівняти попарно всі 0-куби, одержуємо множину 1-кубів К1. Застосовуючи…

К={К0, К1,..., КS}, де s£n-1.

Для виділення з К₀ множини простих імплікант ZÌK при кожній операції склеювання тим чи іншим способом відзначаються ті куби, що поєднуються в куби вищої розмірності. Очевидно, що невідмічені куби й утворять множину простих імплікант Z, іменовану скороченою ДНФ.

На наступному кроці при витягу екстремалей використовується таблиця покрить. Її рядки відповідають простим імплікантам, а стовпці - конституентам «1» (0-кубам) даної функції. У клітці таблиці ставиться мітка, якщо проста імпліканта, що відповідає даному рядку, покриває вершину, яка відповідає даному стовпцю клітки. Екстремалям відповідають ті рядки таблиці, що містять єдину мітку в якому-небудь стовпці. Видаляючи рядки екстремалей і всі стовпці, в яких дані рядки мають мітки, одержуємо скорочену таблицю покрить.

Зі скороченої таблиці покрить тим чи іншим способом вибираються прості імпліканти, що доповнюють виділену множину екстремалей до тупикових покрить. Метод Квайна не формалізує цей крок у вигляді якої-небудь процедури. На множини всіх тупикових покрить визначаються мінімальні покриття, яких може бути кілька.

Приклад. Задана функція y=Ú¹(0, 1, 2, 5, 6, 7). Комплекс кубів містить три множини, з яких К₁ дорівнює скороченої ДНФ,
табл. 17.1 ілюструє покриття простими імплікантами зі СкДНФ конституент 1.

К = 000 К₁ = 00´ К₂ = Æ

001 0´0 СкДНФ = К₁

010 ´01

101 ´10

110 1´1

111 11´

Таблиця 27.1

	000	001	010	101	110	111
00´	Ú	Ú					A
0´0	Ú		Ú				В
´01		Ú		Ú			С
´10			Ú		Ú		D
1´1				Ú		Ú	E
11´					Ú	Ú	F
	AÚB	AÚC	BÚD	CÚE	DÚF	EÚF

У прикладі екстремалі відсутні (Екстремалі з'являться у наступному прикладі лекції 18). Тупикові ДНФ мають вид:

ТДНФ₁= 00´ ТДНФ₂= 00´ ТДНФ₃= 0´0

0´0 ´10 ´01

1´1 1´1 11´.

11´

Мінімальні ДНФ і їхньої ціни по Квайну мають вид:

МДНФ₁=ТДНФ₂,

Смднф₁=3(n-1)=6, y_min1=`x<sub>2</sub>`x₃Ú`x₁ x₂Ú x₁ x₃,

МДНФ₂=ТДНФ₃,

Смднф₂=3(n-1)=6, y_min2=`x<sub>1</sub>`x₃Ú x₁`x₂Úx₂ x₃.

27.3. Алгебраїчний метод одержання мінімального покриття (алгоритм Петрика)

Вибір мінімального покриття на заключному етапі формалізується за допомогою алгебраїчного методу, що запропонований Петриком. Вихідна форма для алгоритму – таблиця покрить. Прості імпліканти позначаються Якіми-небудь символами, наприклад, літерами латинського алфавіту. У кожнім стовпці таблиці записується диз'юнкція простих імплікант, що покривають відповідний 0-куб. Покриттю функції відповідає кон'юнкція всіх записаних диз'юнкцій векторів.

Якщо спростити отримане вираження за допомогою тотожностей булевої алгебри, одержуємо деяку ДНФ, кожен член якої відповідає деякому тупиковому покриттю. Вибір тих з них, що містять мінімальну кількість букв або мінімальну ціну за Квайном, дає можливість знайти мінімальні покриття.

Приклад. З попередньої таблиці і ряду спрощень при розкритті дужок випливає таке:

Множина ТДНФ: (АÚВ)(АÚС)(ВÚD)(CÚE)(DÚF)(EÚF)=…=

=ADEÚABEFÚBCDEÚBCEFÚACDFÚABCFÚBCDFÚBCF...

Підкреслені кон'юнкції, що мають найменшу ціну і відповідають доповненням ядра до МДНФ. Тому що ядро (множина екстремалей) порожнє, самі підкреслені кон'юнкції й утворюють множину МДНФ.

Алгебраїчні перетворення спрощуються, якщо виходити зі скороченої таблиці покрить, що одержана після виділення екстремалей та знищення рядків екстремалей і стовпців усіх покритих екстремалями конституент, це буде проілюстровано у наступному прикладі лекції 28.

Результатом перетворень є множини простих імплікант, що доповнюють сукупність екстремалей до тупикових покрить. Мінімальне з цих доповнень разом з ядром утворить мінімальне покриття функції.

Контрольні запитання

2. Які змінні називаються зв'язаними, а Які вільними, як позначають у кубі зв'язані та вільні змінні? 3. Чи є комплекс кубів мінімальним покриттям? 4. Що є тупиковим покриттям, а що мінімальним?

Основна

2. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… 3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. -… Додаткова

Вступ

Лекція має за мету навести додаткові методи аналітичної мінімізації скрізь визначених і часткових булевих функцій. Розглянути модифікований метод Квайна-МакКласкі, таблична і аналітична мінімізація частково визначених функцій. Основну увагу звернено до скорочення дій з комплексом кубів, використання у різних методах мінімізації наборів, на яких функція не визначена.

У лекції присутні два підрозділи:

28.1. Модифікований метод Квайна-МакКласкі.

28.2. Мінімізація частково визначених функцій.

28.1. Метод Квайна-МакКласкі

Недоліком методу Квайна є велике число порівнянь, яких необхідно проводити між імплікантами кожного з кубів К_S.

Метод Квайна-МакКласкі є модифікацією методу Квайна, що дозволяє зменшити число порівнянь. Для розв’язання цієї задачі кожна множина К_S розбивається на класи, у кожному з Якій містяться S-куби з однаковим числом одиниць. Класи упорядковуються, наприклад, за зростанням числа одиниць або нулів. Оскількі склеюватися можуть тільки такі два S-куби, число одиниць у яких відрізняється на одну одиницю, то досить обмежитися попарним порівнянням S-кубів деякого класу з
S-кубами сусіднього класу. В іншому модифікація працює так само, як і метод Квайна і для ДНФ, і для КНФ.

Приклад. Нехай чисельним способом задана булева функція від чотирьох змінних у=Ú¹(3, 4, 5, 6, 7, 9, 11, 12, 13). Комплекс з трьох множин K={К¢₀, К¢₁, К₂} і відзначена відповідно до алгоритму Петрика таблиця покрить (табл. 28.1) мають такий вигляд:

К₀= 0011 К¢₀= 0100 К¢₁= 010´ К₂={´10´} К₃=Æ

0100 - - - - ´100

0101 0011 - - - -

0111 0101 0´11

1001 1001 ´011

1011 1100 01´1

1100 - - - - ´101

1101 0111 10´1

1101 110´.

 

 

Таблиця 28.1

	0011	0100	0101	0111	1001	1011	1100	1101
0´11	Ú			Ú					А
01´1			Ú	Ú					В
´011	Ú					Ú			С
10´1					Ú	Ú			D
1´01					Ú			Ú	E
´10´		Ú	Ú				Ú	Ú	H
	AÚC			AÚB	DÚE	CÚD

 

Існує єдина екстремаль - ´10´. Зі скороченої таблиці покрить (табл. 28.2), що може бути отримана з повної таблиці викресленням екстремалей та усіх покритих екстремалями конституент і містить перший, четвертий, п'ятий і шостий стовпці і перший – п'ятий рядки,

Таблиця 28.2

	0011	0111	1001	1011
0´11	Ú	Ú			А
01´1		Ú			В
´011	Ú			Ú	С
10´1			Ú	Ú	D
1´01			Ú		E
	AÚC	AÚB	DÚE	CÚD

 

випливає формула

(AÚC)(AÚB)(DÚE)(CÚD)=(AÚABÚACÚBC)(CDÚCEÚDÚDE)=(AÚBC)(DÚCE)=ADÚACEÚBCDÚBCE.

Таким чином, існує чотири тупикових покриття:

ТДНФ₁ = ´10´ ТДНФ₂ = ´10´ ТДНФ₃ = ´10´ ТДНФ₄ = ´10´

0´11 0´11 01´1 01´1

10´1 ´011 ´011 ´011

1´01 10´1 1´01

МДНФ = ТДНФ₁ ´10´

0´11

10´1.

Ціна за Квайном для усіх ТДНФ має вигляд

Стднф₁=Смднф=1×2+2×3=8 Стднф₂=1×2+3×3=11
Смднф₃=1×2+3×3=11 Стднф₄=1×2+3×3=11.

28.2. Мінімізація частково визначених функцій

Визначення. Частково визначеною функцією називається функція, визначена не на всіх наборах значень змінних.

Частково визначені функції зустрічаються, коли деякі з наборів, що використовують при мінімізації, не застосовуються, якщо додатково визначають функцію на байдужих наборах для економічної реалізації.

Нехай дана частково визначена функція y=f(x₁, x₂,..., x_n). Тоді y¹=f¹(x₁, x₂,..., x_n) - функція, додатково визначена на всіх байдужних наборах одиницями; y⁰=f⁰(x₁, x₂,..., x_n)- функція, додатково визначена на всіх байдужих наборах нулями.

Задача довизначення даної функції для ДНФ зводиться до вибору зі скороченого покриття функції у¹ (для КНФ - до вибору зі скороченого покриття функції у⁰) мінімальної кількості кубів максимальної розмірності, сукупність яких покривала б усі вершини функції у. Така сукупність кубів і утворює мінімальне покриття булевої функції у.

Приклад. Задані функція у=Ú¹(5, 6, 7, 13) і її невизначені набори
´(0, 4, 8, 15). Карта Карно дає представлення про мінімізацію

Таблиця 28.3

У x1,x2 x3x4
	´0	´1		´0
			´1

 

З карти Карно з урахуванням байдужих наборів випливає формула y=`x₁x₂Úx₂x₄. Комплекс кубів Квайна (підкреслені невизначені куби) і таблиця покрить (табл. 18.4) мають вигляд:

К₀= 0000 К₁= 0´00 К₂= 01´´

0100´000 ´1´1

1000 010´

0101 01´0 К₃=Æ

0110 01´1

0111 ´101

1101 011´

1111 011´

´111

11´1

 

Таблиця 28.4

	0101	0110	0111	1101
01xx	Ú	Ú	Ú		A
x1x1	Ú		Ú	Ú	B
	AÚB	A	AÚB	B

 

З таблиці покрить випливає існування двох екстремалей 01xx і x1x1, що утворюють ядро і покривають усі конституенти 1 функції, отже, МДНФ має вигляд y_min=`x₁ x₂ Ú x₂ x₄.

Приклад. Мінімізацію той самої часткової функції можна виконати для КНФ: у=Ù⁰(1, 2, 3, 9, 10, 11, 12, 14) і її невизначені набори ´(0, 4, 8, 15).

Модифікований комплекс кубів для методу Квайна-МакКласкі (підкреслені невизначені куби) і таблиця покрить (табл. 18.5) мають вигляд

К₀= 0000 К₀= 0000 К₁= 0´00 К₂= ´´00 К₃= ´0´´ К₄= Æ

0100 ---- ´000 ´00´

10000100 000´ ´0´0

0001 1000 00´0 00´´

0010 0001 ---- ----

0011 0010 ´100 10´´

1001 ---- 100´ 1´´0

1010 0011 10´0 ´0´1

1011 1001 1´00 ´01´

1100 1010 00´1 ----

1110 1100 ´001 1´1´.

1111 ---- 001´

1011 ´010

1110 ----

---- ´011

1111 10´1

101´

1´10

11´0

----

1´11

111´

Скорочена форма комплекса, містить чотири куби ´0´´, ´´00, 1´´0, 1´1´, а таблиця покрить Квайна має вигляд

Таблиця 28.5

	0001	0010	0011	1001	1010	1011	1100	1110
´0´´	Ú	Ú	Ú	Ú	Ú	Ú			A
´´00							Ú		B
1´´0					Ú		Ú	Ú	С
1´1´					Ú	Ú		Ú	D
	A	A	A	А	АÚСÚD	АÚD	BÚС	CÚD

 

З таблиці покрить випливає існування екстремалі ´0´´, що утворює ядро, останні два стовпця покриває 1´´0, отже y_min=`x₁x₄ Ú x₂. Тобто МКНФ краще, ніж МДНФ.

Контрольні запитання

2. Як у методі Квайна-МакКласкі розбити множини кубів на класи? 3. Що є частково визначеною функціей? 4. Як загально сформулювати задачу довизначення часткової функції?

Основна

2. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… 3. Горбатов В.А. Основы дискретной математики. – М.: Высш. шк., 1986. -… Додаткова

Нтервальне представлення в матричній формі

Приклад. Інтервал [0010, 0110] - це два набори 0010 й 0110, інтервал [0010, 1011] - це чотири набори 0010, 0011, 1010, 1011. Змінні, що приймають однакові значення в «Мін», «Макс» наборах, мають однакове… Визначення. Інтервал – це сукупність 2k наборів, в яких n-k зовнішніх змінних приймають однакові для всіх наборів…

Спрощення ДНФ за матричною формою Закревського

Визначення. Віссю симетрії за змінною xi називається лінія зміни значення цієї змінної за матричною формою. Для деяких змінних у матричній формі… Приклад. У матричній формі виділені осі симетрії всіх змінних і показані для… Таблиця 29.5 x3 x3 x2 …

Лема. Елементи матричної форми, які відповідають наборам, що склеюються, розташовані симетрично щодо осі симетрії змінної, за якою набори склеюються, і в зоні її дії.

Властивість симетрії дозволяє дати нове визначення інтервалу.

Визначення. Інтервал – це сукупність 2^k елементів матричної форми, симетрично розташованих по k осях внутрішніх змінних у зоні їхньої дії.

Інтервал належить функції, якщо на всіх його елементах функція дорівнює одиниці для ДНФ (нулю для КНФ) або не визначена (для часткових функцій). Інтервал називається максимальним, якщо він належить функції, але при симетруванні його по кожній з осей зовнішніх змінних відбувається поглинання елементів, на яких функція дорівнює нулю для ДНФ (одиниці для КНФ).

Приклад. Максимальні інтервали з виділенням осей внутрішніх змінних, по яких елементи інтервалів становлять симетричну фігуру (табл. 29.6).

Таблиця 29.6

					x3	x3
			x2	x2			x2	x2
		x1	x1	x1	x1	x1	x1	x1	x1
	x4|			·	·	·	·
x5|	x4|			·	·	·	·
x5|	x4|
	x4|	·			·	·			·

Сукупність 2² елементів (табл. 29.7) не є інтервалом, тому що ця фігура не симетрична щодо осей симетрії елементів у зоні їхньої дії. Елементи, позначені «а», симетричні по осі х₃, тому інші елементи, позначені «в», щоб формувати інтервал, повинні бути симетричні по цій же осі, але це не так. Елементи, позначені «в», симетричні по осі х₂, тому елементи, позначені «а», повинні мати в інтервалі симетричні елементи по осі х₂, але це також не так.

Таблиця 29.7

					x3	x3
			x2	x2			x2	x2
		x1	x1	x1	x1	x1	x1	x1	x1
	x4|
x5|	x4|				а·	а·	в·	в·
x5|	x4|
	x4|

 

На другому кроці виконується побудова максимальних інтервалів. Визначаються безлічі X^m_пвп потенційно внутрішніх змінних для виділеного елемента m з безлічі М – змінних, по осях симетрії яких для вихідної точки симетрично розташовані сусідні точки або невизначені елементи (~). Потенційно внутрішні змінні так називаються, тому що вихідна точка може склеїтися, утворивши інтервал з кожним зі своїх сусідів, і тоді відповідна змінна стане внутрішньої. Не завжди все потенційно внутрішні змінні можуть одночасно бути внутрішніми в одному інтервалі.

Приклад.

У клітках матриці показане число сусідів для всіх точок. Безлічі Х_пвп для: 11000 – х₁, х₃, х₄, х_5, 00010 – х₁, х₂, х₃, 10110 – х₁, х₃, 10001 – х₂, х₃, 11001 – х₁, х₂, х₃, х₄, х₅. Для точки 11000 чотири змінних потенційно внутрішні, але максимальні інтервали покриваючі цю точку, мають кожний внутрішніми тільки деяку підмножину цих змінних: для інтервалу ~1~0~ - x₁, x₃, x₅,для інтервалу ~10~0 – х₁, х₄, для інтервалу 110~~ - х₄, х₅.

Таблиця 29.8

						x3	x3	x3	x3
				x2	x2	x2	x2
			x1	x1			x1	x1
				4·	4·	3·	3·
	x4|	3·	3·	4·	3·			2·	2·
x5|	x4|			3·			2·
x5|			2·	5·	3·	3·	5·	2·

 

Для визначення максимальних інтервалів, що містять задану точку, знаходять максимально сумісні підмножини змінних множин Х_пвп цієї точки.
У цьому пошуку використовується алгоритм граничного перебору на опуклій безлічі трансформуванням процедури перевірки сумісності змінних: змінні сумісні, якщо симетричний для них інтервал належить функції.

Контрольні запитання

2. Як будується матрична двовимірна форма? 3. Що розуміється під інтервалом? 4. Що називають зовнішніми й внутрішніми змінними?

Список літератури

1. Закревский А.Д. Логический синтез каскадных схем. – М.: Наука, 1991. – С.100-123. Додаткова 2. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и…

Формулювання алгоритму побудови максимальних інтервалів для точки

Крок 2. Методом граничного перебору вибирається чергова змінна, за якою перевіряється можливість симетрування поточного інтервалу по осі симетрії… Крок 3. Процедура граничного перебору при переході до побудови наступного… Реалізація використовуе векторне представлення підмножин внутрішніх змінних.

Алгоритм для ДНФ

2. Вибирається елемент mÎM1 з меншим значенням k, якщо таких елементів декілька, то для визначеності алгоритму вибирається перший. 3. Перебувають максимальні інтервали, що містять елемент m, і серед них… 4. Кон’юнкція, що відповідає обраному максимальному інтервалу, записується в результуючу ДНФ. Всі елементи безлічі M1,…

Контрольні запитання

2. Які дії припускає другий крок алгоритму побудови максимальних інтервалів для заданої точки? 3. Які дії припускає третій крок алгоритму побудови максимальних інтервалів… 4. Як працює алгоритм побудови максимальних інтервалів для ДНФ?

Список літератури

1. Закревский А.Д. Логический синтез каскадных схем, – М.: Наука, 1991. – С.123-130. 2. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. -… Додаткова

Лекція 31. Мінімізація систем булевих функцій

Лекція має за мету дати базові методи мінімізації систем булевих функцій. Розглянуто основні визначення, зокрема нове поняття ярлика кон’юнкції,… У лекції присутні чотири підрозділи: 31.1. Основні визначення

Основні визначення

f1(x1,x2,…,xn) f2(x1,x2,…,xn) …

Використання системи булевих функцій для синтезу КС

   

Точний метод мінімізації систем булевих функцій Барті-Полянського

При мінімізації систем булевих функцій склеюються набори, що допускають склеювання і ярлики яких мають непорожній перетин, результату склеювання… 0 1 0 f1f3 0 1 0 f2f3 1 1 0 f1f2 1 1 0 f1f4

Нтуїтивний метод спрощення системи ДНФ за матричною формою

Немає необхідності формулювати весь алгоритм розв’язання, доцільно привести принцип виділення максимальних інтервалів, що підходять відразу для… Нижче наведені дві послідовності (відповідно у табл. 31.3, 31.3, 31.4 і 31.5,…  

Контрольні запитання

2. Що позначають ярлики кон'юнкцій булевих функцій? 3. Що називається простою імплікантою системи булевих функцій? 4. Як використати систему булевих функцій для синтезу КС?

Список літератури

1. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… Для практичних занять 2. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної…

Лекція 32. Інтервальні форми та їхні перетворення

Лекція має за мету дати базові інтервальних форм і їхніх перетворень. Розглянуто системи повністю й неповністю визначених булевих функцій,… У лекції є два підрозділи: 33.1. Інтервальне представлення в ЕОМ

Нтервальне представлення в ЕОМ

32.1.1. Системи повністю визначених булевих функцій Алфавіт визначений як AA = {1, ~}. У цьому випадку вважається, що на всіх… Приклад

Основні операції над інтервальним представленням

Об'єднання інтервалів полягає в спільному розгляді інтервалів, у складанні списку інтервалів. Визначення. Операція об'єднання інтервалів, що являють собою булеву функцію,… 32.2.1. Дослідження ортогональності інтервалів

Контрольні запитання

2. Які алфавіти використовуються для опису систем повністю визначених булевих функцій? 3. Які алфавіти використовуються для опису систем не повністю визначених… 4. Як інтерпретується операція об'єднання інтервалів?

Список літератури

1. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… Для практических занятий 2. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної…

Лекція 33. Використання інтервальних операцій

Лекція має за мету показати можнасті використання операцій при перетвореннях інтервального представлення. Розглянуто перевірку покриття інтервалу… У лекції присутні два підрозділи: 33.1. Використання операцій інтервального представлення

Використання операцій інтервального представлення

Для використання операції «#» здійснюється віднімання з вихідного інтервалу елементів об'єднання інтервалів. Якщо після всіх віднімань є порожня… Приклад Вихідний інтервал Задане об'єднання інтервалів

Метричні властивості диз'юнктивної нормальної форми

1) оцінки складності алгоритмів перетворення форм булевих функцій; 2) оцінки складності дискретних пристроїв, складність схем яких пропорційна… 3) алгоритми виконання обчислень можна виразити через перетворення булевих функцій, булев варіант алгоритму зберігає…

Контрольні запитання

2. У чому посягає процедура розширення інтервалу в заданому об'єднанні інтервалів до максимального? 3. Які кроки містить процедура розширення інтервалу в заданому об'єднанні… 4. Що такє ядерність інтервалу?

Лекція 34. Булеві рівняння й нерівності

Лекція має за мету дати базові методи розв’язання систем булевих рівнянь і нерівностей. Розглянуто основні визначення, зокрема, нове поняття булевих… У лекції присутні три підрозділи: 34.1. Булеві рівняння

Булеві рівняння

f(x1, x2, …, xk) = g (x1, x2, …, xk) є найбільш загальною формою булева рівняння. Розв’язаннями є всі такі вектори… Повинні виконуватися такі відношення

Булеві нерівності

f(x1, x2, …, xk) £ g (x1, x2, …, xk) є самою загальною формою булевої нерівності. Розв’язаннями є всі такі вектори… У цьому випадку повинне виконуватися

Спільні системи нерівностей і рівнянь

f1(x1, x2, …, xk) £ g1(x1, x2, …, xk); … … … fm(x1, x2, …, xk) £ gm(x1, x2, …, xk);

Контрольні запитання

2. Яка властивість й як використовується при розв’язанні булевых рівнянь?Як використовується ця властивість? 3. Що є розв’язанням системи булевых рівнянь? 4. Як можна одержати еквівалентне рівняння для системи булевых рівнянь?

Список літератури

Основна

1. Бохман Д., Постхоф Х. Двоичные динамические системы. – М.: Энергоатомиздат, 1986. - С.60-61.

Для практичних занять

2. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2004. - ч.2. –
С.75-76.

Лекція 35. Булеві різниця, похідні й диференціали

Лекція має за мету надати основні поняття булевих різниці, похідних й диференціалів. Розглянуто визначення булевих різниці, приватної й повної… У лекції є чотири підрозділи: 35.1. Властивості булевой різниці

Властивості булевой різниці

Визначення. Булевой різницями функції F(х1,x2,...,хi,...,xn) щодо змінної хi (d/dхi – булева похідна, оператор різниці) називається вираження виду … d(x)/dхi з= F(x1, х2,..., хi,...,xn) Å F(x1, x2 ,..., `хi,...,хn) Булева різниці використає властивості операції додавання по модулі 2 алгебри Жегалкина, на їхній основі визначаються…

Тотожності булевой різниці

2. d(Х)/dхi = d(Х)/d`хi 3. d(d(Х)/dхj)/dхi = d(d(Х)/dхi)/dхj 4. d(F(Х)G(X))/dхi = F(Х)(d(Х)/dхi) Å G(Х)(d(Х)/dхi) ÅÅ (d(Х)/dхi)(d(Х)/dхi)

Теорема. Щоб F(Х) не залежала від змінної хiе, необхідно й досить виконання умови d(Х)/dхi = 0.

На додаток до наведеного вище тотожностям на підставі теореми можна досить просто одержати нові закони.

7. d(Х)/dх_i = ì 0, якщо F(Х) не залежить від х_i

î 1, якщо F(Х) залежить від х_i.

8. d(F(Х)G(X))/dх_i = F(Х)(d(Х)/dх_i), якщо F(Х) не залежить від х_i.

9. d(F(Х)+G(X))/dх_i = `F(Х)(d(Х)/dх_i), якщо F(Х) не залежить від х_i.

Як очевидні наслідки теореми можна одержати ще три властивості:

10. Якщо d(Х)/dх_i = 0, то зміна х_i ніколи не змінює F(Х) .

11. Якщо d(Х)/dх_i = 1, то зміна х_i завжди змінює F(Х) .

12. Якщо d(Х)/dх_i = G(Х), то зміна в х_i буде викликати зміну в F(Х) при G(Х) = 1.

Приклад. Нехай є логічна схема (див. рис. 35.1). Можна визначити умови, при яких зміна викличе зміну на виході

 

Рис. 35.1. Логічна схема для передачі
зміни із входу х₁ на вихід

Аналіз функції за допомогою законів алгебри Жегалкина дає результат

d(Х)/dх_i = (x1x2+x3)Å (`x1x2+x3) = x1x2 Å x3 Å x1x2x3 Å `x1x2 Å x3 Å Å`x1x2x3 = x2`x3

Однак його можна швидше одержати й за допомогою булевой різниці

d(x1,x2,x3)/dх_i = d(x1x2+x3)/dх_i = `x3d(x1x2)/dх<sub>i</sub> = x2`x3d(x1)/dх_i = x2`x3

Методи знаходження булевой різниці

Визначення. Булевой різницею функції F(х1,x2,...,хi,...,xn) щодо змінної хi називається вираження виду d(x)/dхi = F(x1, х2,..., 1,...,xn) Å F(x1, x2 ,..., 0,...,хn), справедливе для будь-яких хi, 1 £ i £ n.

Якщо F(x) = A(X) +xi(X) + `xi(X), де A(X), B(X) і C(X) не залежать від xi, то справедливо

d(Х)/dх_i = `A(X)(B(X) Å C(X))

Подвійна булева різниця

Визначення. Подвійною булевою різницєю функції F(х1,x2,...,хi,...,хj,...,xn) щодо змінних хi і хj називається вираз виду d2F(Х)/dхidхj = F(x1, х2,..., хi,...,хj,...,xn) Å F(x1, x2… Приклад. Нехай дана функція F(X) = x1+x2+x3, звідси треба, що

Теорема. Щоб F(Х) не залежала від змінних хi і хj, необхідно й досить виконання умови d2F(Х)/dхidхj = 0.

Визначення й теорема справедливі тільки для випадку одночасної появи змін у х_i і х_j, що відмінно від випадку подвійної зміни, тому що останній містить у собі також й одиночні зміни х_i або х_j.

Таким чином, можна виділити випадки:

1. Різниця для визначення реакції на дві зміни в х_i і х_j

d²F(Х)/dх_idх_j = d(Х)/d(х_iх_j) =
= F(х₁,x₂,...,х_i,...,х_j,...,x_n) Å F(х₁,x₂,...,`х<sub>i</sub>,...,`х_j,...,x_n).

2. Різниця для визначення реакції на зміну або в х_i, або в х_j

d(Х)/d(х_iÅх_j) = = d(Х)/dх_i + d(Х)/dх_j.

3. Різниця для визначення реакції на зміну або в х_i, або в х_j, або в х_i і х_j одночасно

d(Х)/d(х_i+х_j) = = d(Х)/d(х_iÅх_j) + d(Х)/d(х_iх_j).

Булеві похідні й диференціали

ðf(x)/ ðхi = f(x0, х1,..., хi,...,xn) Å f(x0, x1 ,..., `хi,...,хn) Тотожним даному визначенню є таке визначення часткової БП: ðf(x)/ ðхi = f(x0, х1,... , хi-1, l, хi+1,…, xn) Åf(x0, х1,... , хi-1, 0, хi+1,…, xn)

Eth;(f(x) Å g(x))/ðхi = `g(x)`g(`x)®ðf(x)/ðхi ÚÚ g(x) g(`x)¬ðf(x)/ðхi Ú `f(x)`f(`x)®ðg(x)/ðхi ÚÚ f(x) f(`x)¬ðg(x)/ðхi.

Властивості прямої й оберненої ОБП можна вивести з цих відношень.

9. [ð`f(x)/ðх<sub>i</sub>]<sub>п</sub> = [ðf(x)/ðх<sub>i</sub>]<sub>про</sub> [ð`f(x)/ðх_i]_про = [ðf(x)/ðх_i]_п

10. [ðf(`x)/ðх<sub>i</sub>]<sub>п</sub> = [ðf(x)/ðх<sub>i</sub>]<sub>про</sub> [ðf(`x)/ðх_i]_про = [ðf(x)/ðх_i]_п

11. [ð(f(x)g(x))/ðх_i]_п = g(x=1)(ðf(x)/ðх_i]_n Ú f(x=1)(ðg(x)/ðх_i]_n

12. [ð(f(x) g(x))/ðх_i]_про =g(x=0)(ðf(x)/ðх_i]_про Ú
Ú f(x=0)(ðg(x)/ðх_i]_про

Eth;(f(x) Ú g(x))/ðхi]п = `g(x=0)(ðf(x)/ðхi]n ÚÚ `f(x=0)(ðg(x)/ðхi]n.

14. [ð(f(x) Ú g(x))/ðх_i]_про = `g(x=1)(ðf(x)/ðх<sub>i</sub>]<sub>про</sub> Ú
Ú `f(x=1)(ðg(x)/ðх_i]_про

15. [ð(f(x) Å g(x))/ðх_i]_п = `g(x=1)`g(x=0)(ðf(x)/ðх_i]_n Ú
Ú g(x=1)g(x=0)(ðf(x)/ðх_i]_про Ú `f(x=1)`f(x=0)(ðg(x)/ðх_i]_n Ú
f(x=1)f(x=0)(ðg(x)/ðх_i]_про

16. [ð(f(x) Å g(x))/ðх_i]_o = `g(x=1)`g(x=0)(ðf(x)/ðх_i]_o Ú
Ú g(x=1)g(x=0)(ðf(x)/ðх_i]_n Ú `f(x=1)`f(x=0)(ðg(x)/ðх_i]_o Ú
Ú f(x=1)f(x=0)(ðg(x)/ðх_i]_n

Приклад. Можна обчислити частки ОБД й ОБП за змінною х₂ функції
f(x) = х₁х₂ Ú `х₂х₃.

Булева похідна, орієнтована на зменшення, за змінною х₂ дорівнює ^¬ðf(х) /ðх₂ = (x_tx₂ Ú `х<sub>2</sub>x<sub>3</sub>) ù(x<sub>1</sub>`x₂ Ú х₂х₃) = х₁х₂`х<sub>3</sub>, Ú `х₁`х₂х₃. Звідси набори х₁ = 1, х₂ = 1, х_э = 0 і х₁ = 0, х₂ = 0, х₃ = 1 визначають умови чутливості функції до змінного х₂. При цьому зміна значення х₂ на протилежне (з 1 в 0 у наборі 110 або з 0 в 1 у наборі 001) приводить до зміни функції з 1 в 0.

Булева похідна, орієнтована на збільшення, по змінній х₂ дорівнює ^®ðf(х) /ðх₂ = ù (x_tx₂ Ú `х<sub>2</sub>x<sub>3</sub>) (x<sub>1</sub>`x₂ Ú х₂х₃) = `х<sub>1</sub>х<sub>2</sub>х<sub>3</sub>, Ú х<sub>1</sub>`х₂`х₃. Звідси зміна змінної х₂ з 1 в 0 у наборі 011 або зміна х₂ з 0 в 1 у наборі 100 приводить до зміни значення функції з 0 в 1.

Пряма й обернена ОБП для змінної х₂ мають вигляд [ðf(х) /ðх₂]_n = х₁`х<sub>2</sub>; [ðf(х) /ðх<sub>2</sub>]<sub>o</sub> = `х₁х₂.

Часткові ОБД визначаються так ^¬d_x2 f(x) = (^¬ðf(х) /ðх₂)dx₂ = (x₁x₂`x<sub>3</sub> Ú x<sub>1</sub>`x₂`x<sub>3</sub>)dx<sub>2</sub> = `x₁x₃ ^¬d_x2 Ú x₁`x<sub>3</sub> <sup>®</sup>d<sub>x2</sub>; <sup>®</sup>d<sub>x2</sub> f(x) =
=(<sup>®</sup>ðf(х) /ðх<sub>2</sub>)dx<sub>2</sub> = (`x₁x₂x₃ Ú x₁`x<sub>2</sub>`x₃)dx₂ = `x<sub>1</sub>x<sub>3</sub> <sup>¬</sup>dx<sub>2</sub> Ú x<sub>1</sub>`x₃ ^®dx₂. З ОБД, орієнтованого на зменшення, треба, що зміна функції з 1 в 0 досягається зміною х₂ з 1 в 0 за умови х₁ = 1, х₃ = 0 або зміною х₂
з 0 в 1 за умови х₁ = 0, х₃ = 1. ОБД, орієнтований на збільшення, дорівнює 1 при зміні х₂ з 1 в 0 при x₁ = 0, х₃ = 1 або при зміні х₂ з 0 в 1 при х₁ = 1, х₃ = 0.

Контрольні питання

2. Які властивості має булева різниця? 3. Чім відрізняються карти Карно і Хсиао Скотта для булевої різниці? 4. Що є подвійною булевою різницею?

Список літератури

1. Селлерс Ф. Методы обнаружения ошибок в работе ЭВМ. – М.: Мир, 1974. - С.32-41. Додаткова 2. Бохман Д., Постхоф Х. Двоичные динамические системы. М.: Энергоатомиздат, 1986. - С.66-167.

Вступ

Лекція має за мету навести базові поняття логікі предикатів. Розглянути висловлення предикатів, аргументи-терми, квантори, зміни арності предикатів, а також правила використання кванторів. Звернено увагу до наведених форм, формул, та використання предикатів.

У лекції присутні три підрозділи:

36.1. Висловлення предикатів

36.2. Логіка предикатів

36.3. Правила застосування кванторів

36.1. Висловлення предикатів

Нехай А и В - деякі висловлення, що можуть бути вірними («1») чи помилковими («0»). Якщо позначити літерами прості висловлення, можна представити складне висловлення за допомогою відповідних логічних операцій.

Приклад. А - «Я піду в театр»,
В - «Я зустріну друга»,
А&В - «Я піду в театр і зустріну друга».

Якщо висловлення вірне, то його заперечення помилкове. Звичайно висловлення виражають властивості одного чи декількох об'єктів.

Приклад. А - «Тиск масла на кульку клапана більше тиску пружини»,
В - «Масло відкриває клапан»,
С - «Масло перетікає з нагнітальної порожнини у впускну» А→В→С.

Змістовна частина висловлення відіграє роль визначальної властивості сукупності об'єктів, для яких це висловлення вірне, і називається предикатом. Предикат являє собою логічну функцію Р(х), що як і булеві функції може приймати значення «0» чи «1», але на відміну від них значення аргументу можуть вибиратися з деякої множини М об'єктів, яку називають областю визначення, тобто хÎМ.

У загальному випадку така функція може бути залежною від багатьох змінних х₁, х₂,..., х_n, що приймають значення з тої самої множини X чи різних множин X₁, X₂,…, і може записуватися як Р(х₁, х₂,..., х_n).

36.2. Логіка предикатів

Аргументи неоднорідних функцій, на відміну від однорідних можуть приймати значення з будь-яких скінченних чи нескінченних множин, але область значень самих функцій обмежена скінченними множинами.

Визначення. N-місцевим предикатом називається неоднорідна двозначна логічна функція від n аргументів вигляду Р(х₁, х₂,.., х_n) з областю значень {0, 1}.

Аргументи N-місцевого, або N-арного предиката являють собою об'єкти з деякої області визначення Х (хÎХ) і називаються предметними змінними. Конкретні значення змінних називаються предметними постійними. Предметні змінні та предметні постійні утворюють клас логічних понять, які називають термами.

Визначення. Термом є: а) деяка предметна змінна або константа;
b) f(f₁, f₂,... f_n), якщо f – функціональна літера та f₁, f₂,... f_n – терми;
c) деякій вираз, коли це слідує з правил a), b).

Приклад. Р(х₁, х₂) - «х₁, х₂ - парні числа», де х₁, х₂ÎХ, Х - множина натуральних чисел. У тому випадку Р(2, 3)=0, тобто ложно, а Р(2, 4)=1, тобто істинно

При заміщенні аргументу «х_і» деякім його значенням «а» N-місцевий предикат Р(х₁, х₂,..., х_n) перетворюється в (N-1)- місцевий предикат Р(х₁, х₂,..., а,..., х_n) і від змінної х_і вже не залежить. N-місцевий предикат, у якому всі х₁, х₂,…,х_n змінних замінені постійними значеннями, перетворюються у висловлення, яке можна розглядати як 0-місцевий предикат.

Приклад. Р(х₁, х₂, х₃) - «х₁ є сумою х₂ і х₃», 3-місцевий,

Р(5, х₂, х₃) - «5 є сумою х₂ і х₃», 2-місцевий,

Р(5, 3, х₃) - «5 є сумою 3 і х₃», 1-місцевий,

Р(5, 3, 2) = 1 - «5 є сумою 3 і 2», - 0-місцевий вірний,

Р(5, 3, 1) = 0 - «5 є сумою 3 і 1» - 0-місцевий помилковий.

У логіці предикатів часто використовуються дві основні операції, що називають кванторами. Нехай Р(х) - предикат, визначений на множини значень аргументу Х.

Визначення. Твердження, що всі хÎХ мають властивість Р(х), записується за допомогою квантора спільності " у вигляді "хÎC Р(х) чи "х Р(х), що читається як «для всіх хÎХ Р(х) - предикат від х - вірний».

Визначення. Твердження, що існує хоча б один об'єкт хÎC, що володіє властивістю Р(х), записується за допомогою квантора існування $ у вигляді $хÎХ Р(х) чи $х Р(х), що читається як «існує хÎC, що Р(х) - предикат від х - вірний».

Квантори ²"² і ²$² зв'язують перемінну х і перетворюють одномісний предикат у висловлення. Очевидно, «"х Р(х)», розглянуте як висловлення, істинне тільки за умови, що Р(х) - тотожно вірний предикат, у всіх інших випадках це висловлення помилкове. «$хР(х)», розглянуте як висловлення, завжди вірне, крім єдиного випадку, коли Р(х) - тотожно помилковий предикат.

Приклад. Нехай Р(х) - «х - просте число», де хÎC і Х - множина натуральних чисел, тоді висловлення:

а) "х Р(х)=0 - «усі натуральні числа прості» - помилкове;
б) $х Р(х)=1 - «існує просте натуральне число» - вірне.

Застосування квантора до N-місцевого предиката перетворює останній у (N-1)- місцевий предикат та знижує його арність. У загальному випадку можливе застосування до одного N-місцевого предиката декількох кванторів. Якщо до N-місцевого предиката застосувати
k-кванторів, де k≤n, то предикат перетворюється в (N-k)- місцевий предикат, якщо k=n, то предикат перетворюється у висловлення. Змінні, до яких застосовуються квантори, називаються зв'язаними, інші змінні називаються вільними.

Приклад : "хР(х, у) - 1-місцевий предикат, "х$уР(х, у) – 0-місцевий предикат, або висловлення.

36.3. Правила застосування кванторів

1. Однойменні квантори можна переставляти місцями

"х "у Р(х, у) = "у "х Р(х, у);

$х $у Р(х, у) = $у $х Р(х, у)

2. Різнойменні квантори в загальному випадку переставляти не можна

"х $у Р(х, у) ¹ $у "х Р(х, у)

3. Між кванторами спільності ²"² і існування ²$² мають місце співвідношення, що узагальнюють закони деМоргана.

ù("х Р(х)) = $хù(Р(х));

ù($х Р(х)) = "х ù(Р(х))

Вираження, які можна утворювати застосуванням до предикатів зв'язувань і кванторів, являють собою формули логіки предикатів. Під логічними зв'язуваннями розуміються слова «не», «і», «чи», «якщо..., то...», «якщо і тільки якщо...». Оскількі предикати - це двозначні логічні функції, то кожному з цих зв'язувань відповідає своя логічна операція - заперечення, кон'юнкції, диз'юнкції, імплікації, еквівалентності відповідно.

Визначення. Предикатною формулою є: a) деяка елементарна формула; b) кожен з виразів А°В та "хÎM(A(x)), якщо А і В формули та х – предметна змінна (° - зв'язка послідовності висловлень); c) деякій вираз, коли це випливає з правил a), b).

У математиці предикати і формули логіки предикатів широко використовуються для символізації запису властивостей, визначень, відношень. Переклад пропозицій з якої-небудь розмовної мови на символічну мову логіки предикатів є нетривіальним через відсутність «механічних» правил. Цей переклад заснований не стільки на формі звичайних пропозицій, скільки на виявленні їхнього зв'язку значень.

Приклад. Нехай Р(х₁, х₂) - бінарне відношення j, визначене на множині Х. При розгляді його як двомісного предиката можна записати властивості відношень:

а) рефлективність: "х Р(х, х) чи "х (хjх);

б) симетричність: "х₁ "х₂(Р(х₁, х₂)ÞР(х₂, х₁₎)

чи "х₁ "х₂((х₁jх₂)Þ(х₂jх₁));

в) транзитивність: "х₁ "х₂ "х₃((Р(х₁, х₂)&Р(х₂, х₃))ÞР(х₁, х₃))

чи "х₁ "х₂ "х₃(((х₁j х₂)&(х₂j х₃))Þ(х₁j х₃)).

Формули логіки предикатів, у яких заперечення відносяться тільки до елементарних предикатів чи висловлень, причому з логічних операцій містяться тільки операції булевого базису {Ú, Ù, ù}, називаються приведеними чи майже нормальними формами.

Приклад. "х₁ "х₂(Р(х₁, х₂)ÞР(х₂, х₁)) - неприведена формула;
ù("х Р(х)) - не приведена формула;
"х ù(Р(х, х)) - приведена формула;
"х₁ "х₂ (Р(х₁, х₂)ÙùР(х₂, х₁))Ú ù ( Р(х₁, х₂)ÙР(х₂, х₁)) – не- приведена формула.

За допомогою предикатів можна здійснити запис функцій.

Приклад. Для n-входового кон'юнктора (схеми, що реалізує кон'юнкцію від n змінних) y=Ù(x₁, x₂,…,x_i,…,x_n) запис за допомогою предикатів виглядає

"х_і P(x_i) Þ P(y).

Для n-входового диз'юнктора (схеми, що реалізує диз'юнкцію від n змінних) y=Ú(x₁, x₂,…,x_i,…,x_n) запис за допомогою предикатів виглядає

$х_і P(x_i) Þ P(y).

Для функції y = ùx₁ x₂ Ú x₂ x₄ запис за допомогою предикатів, хоч і трохи громіздко, але виглядає

$ (x₁, x₂) (((ùP(x₁) і P(x₂)) чи (P(x₂) і P(x₄))) Þ P(y).

Для n-входової схеми нерівнозначності (схеми, що реалізує складення по модулю “2” від n змінних) y=Å(x₁, x₂,…,x_i,…,x_n) запис за допомогою предикатів такий:

("(х_і1, х_і2, ..., х_і2k+1) P(x_im))&("(х_j1, х_j2, ..., х_j2r) P(x_jt))ÞùP(y),
де m<2k+1<n та t<2r<n.

 

Контрольні запитання

2. Що є предметними змінними та предметними постійними, яка між ними різниця? 3. Що є термом, які три правила формально визначають терм? 4. Які операції використовують у логіці предикатів, як виконати перехід від неформального словесного опису к…

Основна

2. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.78-81. 3. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001.… Додаткова

СПИСОК ЛІТЕРАТУРИ

Основна

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. 3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. 4. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатом-издат, 1987.

Додаткова

14. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.:… 15. Биркгоф Г., Барти Т. Современная прикладная алгебра. – М.: Мир, 1976. 16. Селлерс Ф. Методы обнаружения ошибок в работе ЭВМ. – М.: Мир, 1974.

Для практичних занять

21. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів заочної форми навчання фахів… 22. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. –… 23. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука,…

ЗМІСТ

Вступ3

ТЕОРІЯ МНОЖИН І АЛГЕБРАЇЧНИХ СИСТЕМ4

1.1. Основні поняття і завдання множин 4 1.2. Операції над множинами. Формули. Тотожності 5 1.3. Доказ тотожностей. Булева алгебра множин 6

КОМБІНАТОРИКА65

Лекція 12. Комбінаторика. Базові методи 65

12.1. Вибірка елементів 65

12.2. Правило суми і добутку 66

12.3. Перестановки 66

12.4. Сполучення 67

12.5. Рекурентні співвідношення 68

12.6. Біном Ньютона 69

Лекція 13. Комбінаторика. Додаткові методи 71

13.1. Поліноміальні твірні функції 71

13.2. Експонентні твірні функції 73

13.3. Принцип включення і виключення 74

13.4. Розбивки 75

ГРАФИ78

14.1. Основні визначення 78 14.2. Способи представлення графів 81 Лекція 15. Визначення графів. Зважені графи 86

СКІНЧЕННІ АВТОМАТИ101

18.1. Абстрактний автомат 101 18.2. Способи завдання автоматів 102 18.2.1. Табличний спосіб 102

БУЛЕВА АЛГЕБРА123

Лекція 22. Булеві функції 123

22.2. Булеві функції 123 22.3. Логічні формули 125 Лекція 23. Завдання булевих функцій. Приведення формул 127