Модель делового цикла Самуэльсона-Хикса.
В данном параграфе мы рассмотрим динамический вариант модели Кейнса, известный под названием модели делового цикла Самульсона-Хикса. Если в модели Кейнса используется принцип независимого (от величины национального дохода) характера инвестирования, то в модели Самуэльсона-Хикса используется так называемый принцип акселерации, т. е. предположение, что масштабы инвестирования прямо пропорциональны приросту национального дохода. Данное предположение характеризуется следующим уравнением
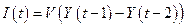 , ,
| (4.1) |
где 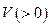 - фактор акселерации,
- фактор акселерации, 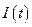 - величина инвестиций в период
- величина инвестиций в период  ,
, 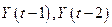 - величины национального дохода соответственно в
- величины национального дохода соответственно в 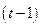 -м и
-м и 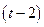 -м периодах.
-м периодах.
Естественно также предположить, что спрос на данном этапе зависит от величины национального дохода на предыдущем этапе, т.е., что
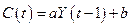 . .
| (4.2) |
Условие (2.1) равенства спроса и предложения в динамическом варианте имеет вид:
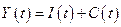 . .
| (4.3) |
Подставляя в (4.3) выражения для 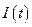 из (4.1) и выражения для
из (4.1) и выражения для 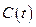 из (4.2) , находим:
из (4.2) , находим:
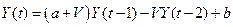 . .
| (4.4) |
Уравнение (4.4) известно как уравнение Хикса. Оно представляет собой линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами (если предположить, что на протяжении рассматриваемых периодов величины a и V постоянны).
Замечание 4.1.Методы решения данного класса уравнений во многом аналогичны решению линейных дифференциальных уравнений с постоянными коэффициентами. Так, общее решение уравнения (4.4) определяется по формуле
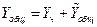 , ,
| (4.5) |
где 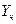 - некоторое частное решение уравнения (4.4),
- некоторое частное решение уравнения (4.4),  - общее решение соответствующего однородного уравнения (т. е. в предположении, что
- общее решение соответствующего однородного уравнения (т. е. в предположении, что 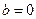 ), в нашем случае это уравнение:
), в нашем случае это уравнение:
 . .
| (4.6) |
Замечание 4.2.Для нахождения общего решения уравнения (4.6) необходимо сперва решить характеристическое уравнение
 . .
| (4.7) |
После этого могут возникнуть три варианта.
1) Оба корня 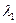 и
и  действительны и различны. Тогда общее решение находится по формуле:
действительны и различны. Тогда общее решение находится по формуле:
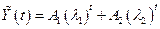 , ,
| (4.8) |
где 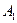 и
и 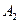 - произвольные константы,
- произвольные константы,  - положительное целое число.
- положительное целое число.
2) Оба корня действительны и равны 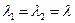 , тогда
, тогда
. 
| (4.9) |
3) В случае комплексно сопряженных корней
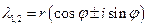
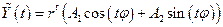 . .
| (4.10) |
Замечание 4.3.Чтобы определить константы А1 и А2, необходимо задать начальные условия
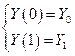 . .
| (4.11) |
В нашем случае это означает, что необходимо зафиксировать первоначальный уровень национального дохода  и уровень национального дохода
и уровень национального дохода 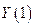 на первом этапе.
на первом этапе.
Замечание 4.4.Мы можем легко найти частное решение уравнения (4.4), если положим, что
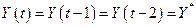 , ,
| (4.12) |
т. е. использовав в качестве частного решения равновесное решение  . Имеем
. Имеем 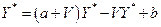 . Откуда
. Откуда
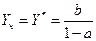 . .
| (4.13) |
Пример 4.1.Рассмотрим модель Самуэльсона при условии, что 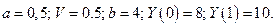 В этом случае на основании (4.13) получаем, что частным решением (4.4) будет
В этом случае на основании (4.13) получаем, что частным решением (4.4) будет
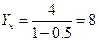 . .
| (4.14) |
Найдем корни характеристического уравнения
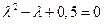 . .
| (4.15) |
Имеем 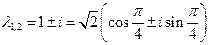 . Таким образом,
. Таким образом,
 .
.
А следовательно, в силу (4.5) и (4.14),
 .
.
Учитывая, что  и
и 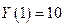 , получаем
, получаем

Откуда находим, что  и
и  . Следовательно,
. Следовательно,
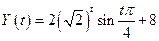 .
.
Замечание 4.5.В зависимости от значений  и
и 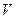 возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный с возрастающей амплитудой характер. Мы рекомендуем читателю самостоятельно определить виды динамики в зависимости от
возможны четыре типа динамики. Она может быть растущей или затухающей и при этом иметь или не иметь колебательный характер. Так, в рассмотренном выше примере динамика носила колебательный с возрастающей амплитудой характер. Мы рекомендуем читателю самостоятельно определить виды динамики в зависимости от  и
и 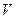 .
.
Замечание 4.6.Если 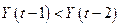 , то из (4.1) следует, что
, то из (4.1) следует, что  . Это означает, что основные фонды уменьшились на величину
. Это означает, что основные фонды уменьшились на величину 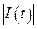 .
.
Замечание 4.7.В некоторых более общих моделях в правую часть уравнений (4.8) могут вводиться дополнительные слагаемые (например, величина государственных расходов G(t)), т. е.
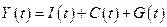 . .
| (4.16) |
В силу этого уравнение Хикса (4.4) принимает вид:
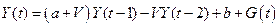 . .
| (4.17) |
При этом часто постулируется, что государственные расходы имеют постоянный темп роста  , т. е., что
, т. е., что
 . .
| (4.18) |
Или, что то же самое,
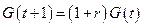 . .
| (4.19) |
Отсюда нетрудно найти, что
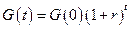 . .
| (4.20) |
Частное решение уравнения Хикса в данном случае следует писать в виде
 . .
| (4.21) |
где  - некоторая константа.
- некоторая константа.
Пример 4.2.В модель Самуэльсона-Хикса, рассмотренную в примере 4.1, внесем следующие изменения, положив, что  и
и 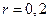 (отсюда следует, что
(отсюда следует, что 
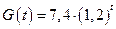 ) и соответственно изменив начальные условия:
) и соответственно изменив начальные условия:
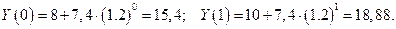
Уравнение Хикса в данном случае принимает вид
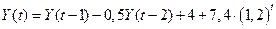 . .
| (4.22) |
Частное решение (4.22) на основании (4.21) будем искать в виде:
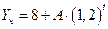 . .
| (4.23) |
Подставляя это выражение для  в (4.17), находим
в (4.17), находим
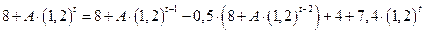 .
.
Отсюда после упрощений получаем, что
 ,
,
или 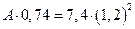 , т. е.
, т. е. 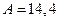 . Следовательно,
. Следовательно,  .
.
Очевидно, что характеристическое уравнение в данном случае будет совпадать с характеристическим уравнением (4.15), рассмотренным в примере 4.1. Поэтому.
 .
.
Положив здесь 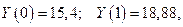 получим, что
получим, что  и
и  , т. е.
, т. е.
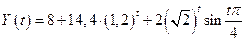 .
.