Линейная модель обмена
1.В данном параграфе мы рассмотрим линейную модель обмена, известную также под названием модели международной торговли. Пусть 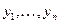 - национальные доходы стран
- национальные доходы стран 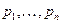 соответственно,
соответственно, 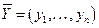 - вектор национальных доходов:
- вектор национальных доходов: 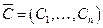 - вектор потребления,
- вектор потребления, 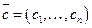 - вектор нормы потребления (
- вектор нормы потребления (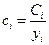 ), показывающий какую часть своего дохода страны тратят на потребление;
), показывающий какую часть своего дохода страны тратят на потребление; 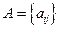 - структурная матрица торговли (элемент
- структурная матрица торговли (элемент 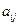 матрицы
матрицы  показывает какую часть национального дохода страна
показывает какую часть национального дохода страна 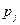 тратит на закупку товаров у страны
тратит на закупку товаров у страны 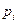 ). Таким образом, страна
). Таким образом, страна 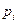 в результате продажи товаров получит доход
в результате продажи товаров получит доход
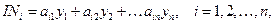
| (5.1) |
или в матричном виде
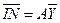 , ,
| (5.2) |
где 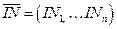 - вектор дохода от продажи.
- вектор дохода от продажи.
В данном пункте мы будем исходить из трех предположений.
1) Рассматриваемая экономическая система замкнута, т. е. все страны покупают товары только друг у друга. Данное условие в наших обозначениях может быть записано следующим образом:
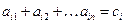 . .
| (5.3) |
Это показывает, что сумма элементов 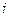 -го столбца матрицы
-го столбца матрицы  равна
равна 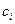 . Уравнение (5.3) в матричной форме выглядит nак
. Уравнение (5.3) в матричной форме выглядит nак
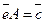 , ,
| (5.4) |
где 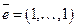 .
.
2) Национальные доходы всех стран полностью тратятся на потребление 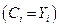 . Следовательно,
. Следовательно, 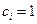 , т. е.
, т. е.
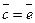 . .
| (5.5) |
В силу последнего соотношения условие (5.4) эквивалентно условию
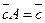 . .
| (5.6) |
Замечание 5.1.Так как 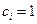 , то из (5.3) вытекает, что все суммы элементов столбцов матрицы
, то из (5.3) вытекает, что все суммы элементов столбцов матрицы  равны
равны 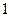 . Отсюда на основании следствия 1.5 вытекает, что число Фробениуса
. Отсюда на основании следствия 1.5 вытекает, что число Фробениуса 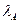 матрицы
матрицы  равно
равно 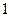 . Поэтому из (5.6) вытекает, что
. Поэтому из (5.6) вытекает, что 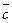 является левым вектором Фробениуса структурной матрицы торговли.
является левым вектором Фробениуса структурной матрицы торговли.
3) Национальный доход 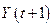 в период
в период 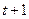 равен доходу от продажи в предыдущем периоде, т. е.
равен доходу от продажи в предыдущем периоде, т. е.
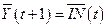 . .
| (5.7) |
С учетом (5.2) последнее условие принимает вид:
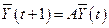 . .
| (5.8) |
Уравнение (5.8) называется уравнением линейного обмена (без учета сбережений). Если  - первоначальный вектор национального дохода, то из (5.8) следует, что в период t вектором национального дохода будет
- первоначальный вектор национального дохода, то из (5.8) следует, что в период t вектором национального дохода будет
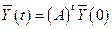
| (5.9) |
(при условии, конечно, что за это время структурная матрица торговли не изменилась).
2. Естественно возникает вопрос, возможна ли в рамках данной экономической системы взаимовыгодная торговля, т. е. существует ли такой вектор 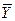 , при котором
, при котором
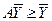 . .
| (5.10) |
Эти соотношения показывают, что все страны получили либо прибыль, либо по крайней мере не имеют убытков. Покажем, что в (5.10) возможен лишь только знак равенства.
Действительно, предположим противное : что в неравенствах (5.10), рассмотренных покоординатно, имеется хотя бы одно строгое неравенство. Тогда просуммировав все эти неравенства, т. е. умножив (5.10) скалярно на 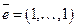 , получим
, получим 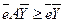 . Учитывая (5.6), получаем
. Учитывая (5.6), получаем 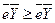 . Мы пришли к противоречию. Следовательно,
. Мы пришли к противоречию. Следовательно,
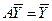 . .
| (5.11) |
С экономической точки зрения данный результат вполне очевиден, т. к. если были бы страны, имеющие прибыль, то в силу замкнутости данной экономической системы, должны быть и страны, имеющие убытки.
Замечание 5.2.Из (5.11) вытекает, что вектор 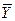 , определяющий равновесное состояние системы, является правым вектором Фробениуса матрицы
, определяющий равновесное состояние системы, является правым вектором Фробениуса матрицы  (т. к.
(т. к. 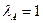 , см. замечание 5.1). Следовательно, для любой модели международной торговли существует равновесное состояние
, см. замечание 5.1). Следовательно, для любой модели международной торговли существует равновесное состояние 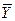 , причем, если матрица - неразложима, то
, причем, если матрица - неразложима, то 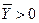 .
.
Замечание 5.3.Т. к. вектор Фробениуса  определен с точностью до знака, то точнее говорить о равновесном распределении доходов. Если структурная матрица торговли
определен с точностью до знака, то точнее говорить о равновесном распределении доходов. Если структурная матрица торговли  неразложима, то равновесное распределение доходов определено однозначно.
неразложима, то равновесное распределение доходов определено однозначно.
Пример 5.1.Пусть структурная матрица торговли имеет вид:
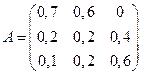 .
.
Определим равновесное распределение национальных доходов. Уравнение (5.11) в данном случае равносильно системе:
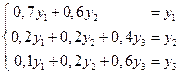 .
.
Решив ее, находим, что 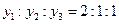 , т. е.
, т. е. 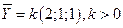 .
.
Замечание 5.4.Из (5.8) и (4.11) вытекает, что, если 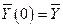 (одному из правых векторов Фробениуса матрицы
(одному из правых векторов Фробениуса матрицы  ), то в результате торговли доходы стран останутся без изменения. Если же
), то в результате торговли доходы стран останутся без изменения. Если же 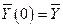 , но существует
, но существует 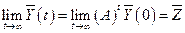 , то из (4.8) следует, что
, то из (4.8) следует, что 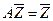 , т. е. то, что
, т. е. то, что 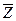 также будем вектором Фробениуса матрицы
также будем вектором Фробениуса матрицы  . Таким образом, вектор Фробениуса
. Таким образом, вектор Фробениуса  определяет не только равновесное , но и предельное состояние системы.
определяет не только равновесное , но и предельное состояние системы.
Замечание 5.5.Можно показать, что если  неразложима и
неразложима и 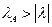 для любого собственного значения
для любого собственного значения 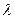 матрицы
матрицы  , то будет существовать предел последовательности
, то будет существовать предел последовательности 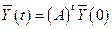 при любом
при любом  (доказательство это факта можно найти в [1]).
(доказательство это факта можно найти в [1]).
Неотрицательные матрицы  , обладающие подобным свойством, называются устойчивыми. Таким образом, если структурная матрица торговли
, обладающие подобным свойством, называются устойчивыми. Таким образом, если структурная матрица торговли  устойчива, то последовательность национальных доходов
устойчива, то последовательность национальных доходов  будет сходится к равновесному состоянию.
будет сходится к равновесному состоянию.
3. В данном пункте мы рассмотрим более общую ситуацию: модель обмена с учетом сбережений. Пусть 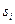 - норма сбережений страны
- норма сбережений страны 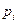 ; (
; (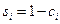 ), - вектор нормы сбережений. Обозначим через
), - вектор нормы сбережений. Обозначим через 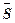 и
и 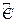 следующие диагональные матрицы:
следующие диагональные матрицы:
а) 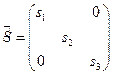 ; б) ; б) 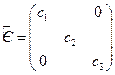 . .
| (5.12) |
Очевидно, что
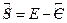 . .
| (5.13) |
Пусть 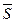 - вектор сбережений, т. е.
- вектор сбережений, т. е. 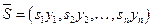 . Как легко видеть
. Как легко видеть
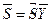 . .
| (5.14) |
В рассматриваемом случае национальный доход 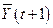 в период
в период 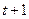 будет складываться из сбережений в период
будет складываться из сбережений в период  и дохода от продажи в период
и дохода от продажи в период  , т. е.
, т. е.
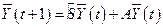 . .
| (5.15) |
или, если подставить в (5.15) выражение для 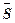 из (5.13),
из (5.13),
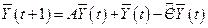 /
/
Последнее условие может записано, как
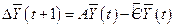 , ,
| (5.16) |
где 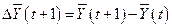 - прирост национального дохода. Требование
- прирост национального дохода. Требование 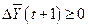 приводит к условию
приводит к условию
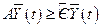 . .
| (5.17) |
Нетрудно, подобно тому, как это делалось выше, показать, что в (5.17) возможен лишь знак равенства. Действительно, из (5.12б) легко получить, что
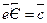 . .
| (5.18) |
Умножим (5.17) скалярно на 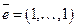 . Тогда, учитывая (5.4) и (5.18), мы получим, что
. Тогда, учитывая (5.4) и (5.18), мы получим, что 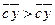 , что невозможно. Значит
, что невозможно. Значит
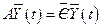 . .
| (5.19) |
А, следовательно, 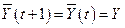 , т. е. данный вектор описывает равновесное состояние системы.
, т. е. данный вектор описывает равновесное состояние системы.
Замечание 5.6.Если вектор нормы сбережений 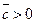 , то нетрудно показать, что определение равновесного дохода, также как и в предыдущем случае, сводится к определению вектора Фробениуса некоторой неотрицательной матрицы. Действительно, если
, то нетрудно показать, что определение равновесного дохода, также как и в предыдущем случае, сводится к определению вектора Фробениуса некоторой неотрицательной матрицы. Действительно, если 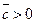 , то из (5.12б) следует, что у
, то из (5.12б) следует, что у 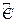 существует обратная матрица
существует обратная матрица
 ,
,
причем 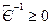 ; тогда, умножив (5.19) на
; тогда, умножив (5.19) на 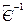 , получим
, получим 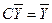 , где
, где 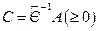 - структурная матрица потребления, элемент
- структурная матрица потребления, элемент 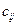 которой показывает, какую часть потребления ci страна
которой показывает, какую часть потребления ci страна 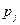 тратит на закупку товаров у страны
тратит на закупку товаров у страны 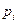 .
.
Замечание 5.7.В случае, когда 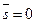 (отсутствие сбережений) структурная матрица потребления
(отсутствие сбережений) структурная матрица потребления 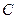 совпадает со структурной матрицей торговли
совпадает со структурной матрицей торговли  .
.
Замечание 5.8. Нетрудно показать, что левым вектором Фробениуса матрицы 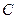 является вектор нормы потребления
является вектор нормы потребления 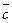 .
.