Продуктивность модели Леонтьева
Рассмотрим экономическую систему, состоящую n отраслей, каждая из которых производит однородный продукт. Пусть 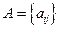 - матрица прямых затрат (матрица Леонтьева), ее элементы
- матрица прямых затрат (матрица Леонтьева), ее элементы 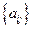 показывают, какое колличество продукции отрасли
показывают, какое колличество продукции отрасли 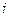 затрачивается на производство единицы продукции отрасли
затрачивается на производство единицы продукции отрасли 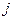 .
.
Обозначим
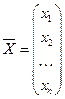 - вектор валового выпуска отраслей,
- вектор валового выпуска отраслей,
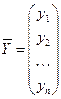 - вектор конечного потребления.
- вектор конечного потребления.
Уравнения межотраслевого баланса, как известно, имет вид:
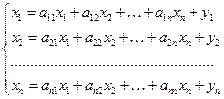 , ,
| (6.1) |
или в матричной форме
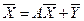 . .
| (6.2) |
Заметим, что 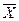 и
и 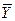 - векторы с неотрицательными компонентами. Основную задачу межотраслевого баланса можно сформулировать следующим образом: зная матрицу Леонтьева
- векторы с неотрицательными компонентами. Основную задачу межотраслевого баланса можно сформулировать следующим образом: зная матрицу Леонтьева  и объемы конечного потребления
и объемы конечного потребления 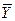 , найти объемы валового выпуска
, найти объемы валового выпуска 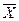 всех oтраслей .
всех oтраслей .
Определение 6.1.Неотрицательная матрица  называется продуктивной, если для любого неотрицательного вектора
называется продуктивной, если для любого неотрицательного вектора 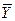 существует неотрицательное решение
существует неотрицательное решение 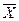 системы (6.2).
системы (6.2).
Имеет место
Теорема 6.1Hеотрицательная матрица  продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
продуктивна тогда и только тогда, когда ее число Фробениуса меньше единицы.
Доказательство. Пусть матрица  — продуктивна. Тогда для любого вектора
— продуктивна. Тогда для любого вектора 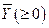 существует решение
существует решение 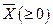 системы (6.2). Пусть
системы (6.2). Пусть 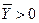 , тогда, очевидно,
, тогда, очевидно, 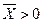 . Умножим равенство (6.2) слева на левый вектор Фробениуса, имеем
. Умножим равенство (6.2) слева на левый вектор Фробениуса, имеем
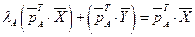 , или
, или 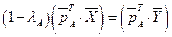 .
.
Так как 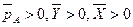 , , то
, , то 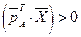 и
и 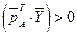 . Поэтому из последнего равенства вытекает, что
. Поэтому из последнего равенства вытекает, что 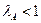 .
.
Обратно, пусть  имеет число Фробениуса
имеет число Фробениуса 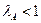 . Покажем, что она продуктивна. Зададим
. Покажем, что она продуктивна. Зададим 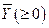 и покажем, что у системы (6.2) существует решение
и покажем, что у системы (6.2) существует решение 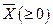 . Рассмотрим следующую неотрицательную матрицу размера
. Рассмотрим следующую неотрицательную матрицу размера 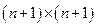
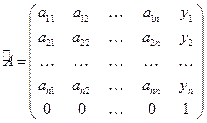 .
.
где 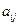 — элементы матрицы
— элементы матрицы  ;
; 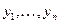 — координаты вектора
— координаты вектора 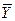 . В более компактной форме матрицу
. В более компактной форме матрицу  можно записать так:
можно записать так:
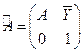 .
.
Умножая эту матрицу слева на 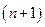 - вектор
- вектор 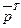 , где
, где 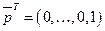 легко убедиться, что
легко убедиться, что 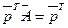 . Следовательно, одно из собственных значений матрицы
. Следовательно, одно из собственных значений матрицы 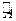 является
является 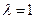 .
.
Пусть вектор 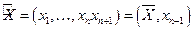 является собственным вектором матрицы
является собственным вектором матрицы 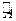 , т.е.
, т.е.  . Это в силу определения матрицы
. Это в силу определения матрицы 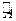 равносильно тому, что
равносильно тому, что
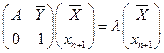 , ,
| (6.3) |
или
 . .
| (6.4) |
Если 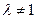 , то из (6.4) следует, что
, то из (6.4) следует, что 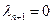 , в силу чего (6.4) примет вид
, в силу чего (6.4) примет вид 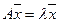 . Следовательно,
. Следовательно, 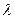 — собственное значение матрицы
— собственное значение матрицы  и, по нашему предположению,
и, по нашему предположению, 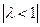 . Таким образом,
. Таким образом, 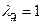 является положительным и максимальным по модулю собственным значением, следовательно, является числом Фробениуса. По теореме Фробениуса-Перрона у матрицы
является положительным и максимальным по модулю собственным значением, следовательно, является числом Фробениуса. По теореме Фробениуса-Перрона у матрицы 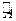 существует неотрицательный собственный вектор
существует неотрицательный собственный вектор 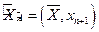 , соответствующий
, соответствующий 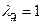 . Очевидно, что
. Очевидно, что 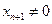 , так как в противном случае из (6.4) следовало бы, что
, так как в противном случае из (6.4) следовало бы, что 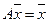 . А это противоречит тому, что число Фробениуса
. А это противоречит тому, что число Фробениуса 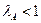 . Поэтому мы можем считать, что
. Поэтому мы можем считать, что 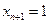 (очевидно, что вектор
(очевидно, что вектор 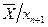 также является вектором Фробениуса). Равенство (6.4) в силу того, что
также является вектором Фробениуса). Равенство (6.4) в силу того, что 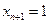 принимает вид
принимает вид 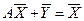 . Причем, так как,
. Причем, так как, 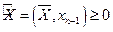 , то
, то 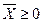 . Следовательно, матрица
. Следовательно, матрица  —продуктивна.
—продуктивна.
Следствие 6.1.Если сумма любого столбца матрицы (любой строки) меньше единицы, то матрица продуктивна.
Справедливость данного утверждения вытекает непосредственно из теоремы 1.2. и теоремы 6.1.
С экономической точки зрения сумму элементов столбца матрицы А можно трактовать как суммарные затраты отрасли на выпуск единицы продукции. Если эти затраты меньше единицы, то отрасль рентабельна. Таким образом, следствие 6.1. утверждает что, если все отрасли рентабельны, то матрица А - продуктивна.