Теория производства.
1.Пусть  - производственная функция, моделирующая зависимость величины выпуска годовой продукции от величины затраченных факторов (ресурсов) производства n
- производственная функция, моделирующая зависимость величины выпуска годовой продукции от величины затраченных факторов (ресурсов) производства n  . Оптимальным планом производства
. Оптимальным планом производства  называется точка максимума функции прибыли
называется точка максимума функции прибыли
 , ,
| (8.1) |
где  - цена единицы выпускаемой продукции (
- цена единицы выпускаемой продукции ( - функция дохода),
- функция дохода), 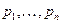 - факторные цены.
- факторные цены.
Множество уровня производственной функции называется изоквантой, а множество уровня функции затрат (издержек) 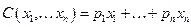 называется изокостой.
называется изокостой.
Неоклассическая производственная функция  - это функция, имеющая непрерывные частные производные второго порядка, удовлетворяющая следующим аксиомам.
- это функция, имеющая непрерывные частные производные второго порядка, удовлетворяющая следующим аксиомам.
1. Аксиома о неотрицательности выпуска
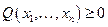
| (8.2) |
при любых неотрицательных значениях факторов.
2. Аксиома об увеличении выпуска при увеличении любого из факторов, т. e.
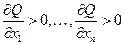 . .
| (8.3) |
3. Аксиома убывающей эффективности факторов (убывающей предельной производительности любого фактора)
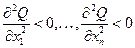
| (8.4) |
при
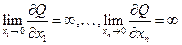 , ,
| (8.5) |
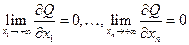 . .
| (8.6) |
4. Аксиома о невозрастающей отдаче на единицу расширения масштаба производства
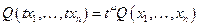
| (8.7) |
для любого  , где
, где 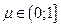 . Величина
. Величина  характеризует эффект от расширения масштаба производства. При
характеризует эффект от расширения масштаба производства. При 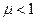 говорят об убывающей отдаче на единицу масштаба, а при
говорят об убывающей отдаче на единицу масштаба, а при  - о постоянной отдаче на единицу масштаба.
- о постоянной отдаче на единицу масштаба.
Замечание 8.1.Функции, удовлетворяющие условию (8.7), называются одно-
родными, при этом  называется степенью однородности. При
называется степенью однородности. При  функцию называю линейно-однородной.
функцию называю линейно-однородной.
Любая однородная функция удовлетворяет условию
 , ,
| (8.8) |
называемому формулой Эйлера.
Основные экономико-математические характеристики производственной функции:
1. Средняя производительность 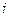 -го фактора
-го фактора

| (8.9) |
2. Предельная производительность 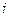 -го фактора
-го фактора
 . .
| (8.10) |
3. Коэффициент эластичности по 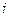 -му фактору
-му фактору
 . .
| (8.11) |
Наибольшее распространение имеют двухфакторные производственные функции 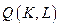 , где
, где 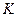 - величина затраченного капитала (основных фондов), а
- величина затраченного капитала (основных фондов), а  - величина затраченного труда. Для двухфакторных моделей дополнительно выделяются следующие характеристики:
- величина затраченного труда. Для двухфакторных моделей дополнительно выделяются следующие характеристики:
4. Фондовооруженность
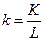 . .
| (8.12) |
5. Предельная норма замещения труда капиталом
 . .
| (8.13) |
6. (Предельная) эластичность замещения труда капиталом
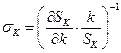 , ,
| (8.14) |
и капитала трудом
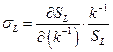 . .
| (8.15) |
2.Утверждение 8.1.Пусть  - функция доходов, а
- функция доходов, а  - функция затрат. Тогда для оптимального плана производства
- функция затрат. Тогда для оптимального плана производства  :
:
а) предельная производительность труда равна реальной заработной плате  ;
;
б) предельная фондоотдача равна реальной рентной плате 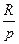 ;
;
в) предельная норма замены труда капиталом равна отношению факторных цен.
Доказательство. Вычислив частные производные функции прибыли  в точке
в точке  имеем
имеем
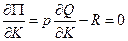 ; ;
| (8.16) |
 . .
| (8.17) |
Отсюда находим:
а)  ; б) ; б) 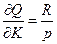 ; в) ; в) 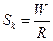 ; ;
| (8.18) |
3. Утверждение 8.2.Пусть 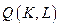 - неоклассическая производственная функция степени однородности
- неоклассическая производственная функция степени однородности  , тогда
, тогда
а) 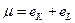 , ,
| (8.19) |
б)  есть норма издержек.
есть норма издержек.
Доказательство. а) Рассмотрим формулу Эйлера для функции 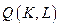
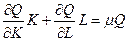 . .
| (8.20) |
Разделив обе части формулы (8.20) на  , находим
, находим
 .
.
Отсюда, на основании определения коэффициентов эластичности по труду и капиталу, получаем (8.19). Из (8.19), в частности вытекает, что неоклассическая производственная функция неэластична ни по труду, ни по капиталу, т. е.
а) 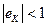 ; б) ; б)  . .
| (8.21) |
Действительно, т. к.  и
и 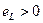 (на основании аксиом 1 и 2) и
(на основании аксиом 1 и 2) и  , то
, то  и
и 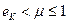 .
.
б) Подставляя в (8.20) выражения 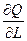 и
и 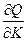 из (8.18а) и (8.18б) соответственно, находим
из (8.18а) и (8.18б) соответственно, находим
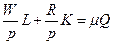 ,
,
т.е. 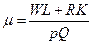 - норма издержек. Здесь
- норма издержек. Здесь  - величина издержек, а
- величина издержек, а  - величина дохода. В частности ,
- величина дохода. В частности , 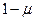 есть норма прибыли.
есть норма прибыли.
4. Утверждение 8.3.В неоклассической модели уровень занятости 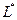 есть убывающая функция от реальной заработной платы.
есть убывающая функция от реальной заработной платы.
Доказательство. Пусть  . Тогда из (8.18а) получаем.
. Тогда из (8.18а) получаем.
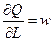 .
.
Дифференцируя последние соотношения по  , находим
, находим
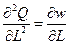 .
.
Так как 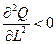 (см. аксиому 3), то
(см. аксиому 3), то 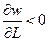 . А, следовательно, на основании теоремы о производной обратной функции
. А, следовательно, на основании теоремы о производной обратной функции 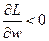 .
.
5. Утверждение 8.4 .Средняя производительность любого фактора неоклассической производственной функции есть убывающая функция от этого фактора.
Доказательство. Дифференцируя (8.9) по  , имеем
, имеем
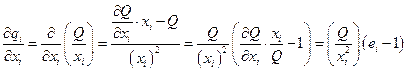 .
.
Так как 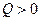 ,
,  ,
,  (неоклассическая производственная функция неэластична по любому фактору, см. (8.21)), то
(неоклассическая производственная функция неэластична по любому фактору, см. (8.21)), то 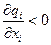 .
.
6. Утверждение 8.5.В точке максимума прибыли норма прибыли имеют нейтральную эластичность.
Доказательство. Пусть  - количество выпускаемой продукции,
- количество выпускаемой продукции,  - величина прибыли,
- величина прибыли, 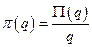 - норма прибыли, т. е
- норма прибыли, т. е 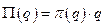 . В точке максимума прибыли имеем
. В точке максимума прибыли имеем
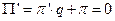 .
.
Отсюда получаем, что 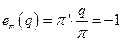 , т.е.
, т.е.  . Это говорит о нейтральной эластичности нормы прибыли.
. Это говорит о нейтральной эластичности нормы прибыли.
Пример 8.1.Пусть 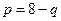 - зависимость между ценой и количеством выпускаемой продукции,
- зависимость между ценой и количеством выпускаемой продукции, 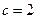 и
и  - соответственно норма переменных издержек и постоянные издержки. Найти оптимальный план выпуска продукции в предположении, что производитель стремится максимизировать прибыль.
- соответственно норма переменных издержек и постоянные издержки. Найти оптимальный план выпуска продукции в предположении, что производитель стремится максимизировать прибыль.
Решение. Из условия задачи следует, что величина дохода производителя равна 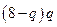 , а издержек -
, а издержек - 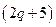 . Таким образом, прибыль
. Таким образом, прибыль  в нашем случае равна
в нашем случае равна  т. е.
т. е.  . Вычислив производную от
. Вычислив производную от  , имеем в точке экстремума
, имеем в точке экстремума 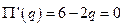 . Следовательно,
. Следовательно,  . Причем, т. к.
. Причем, т. к. 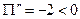 , то
, то  - точка максимума.
- точка максимума.
Пример 8.2.Пусть единица продукции предприятия, рассмотренного в предыдущем примере, облагается акцизным сбором в размере  . Найти, при какой величине
. Найти, при какой величине  суммарный сбор
суммарный сбор 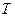 будет максимален.
будет максимален.
Решение.Необходимо найти максимум функции 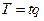 при условии, что предприятие тоже будет стремиться максимизировать свою прибыль. В отличие от предыдущего примера прибыль предприятия уменьшается на величину
при условии, что предприятие тоже будет стремиться максимизировать свою прибыль. В отличие от предыдущего примера прибыль предприятия уменьшается на величину  , т. е.
, т. е.  . Вычислив производную и приравняв ее к нулю, получим в точке максимума
. Вычислив производную и приравняв ее к нулю, получим в точке максимума 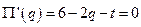 , т. e.
, т. e. 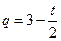 . Поэтому,
. Поэтому,
 .
.
Следовательно,  . Так как в точке максимума
. Так как в точке максимума  , то
, то 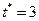 . При этом
. При этом 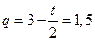 , т. е. в два раза меньше, чем в предыдущей задаче.
, т. е. в два раза меньше, чем в предыдущей задаче.