рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Общая формула для оценки главной части погрешности.
Реферат Курсовая Конспект
Общая формула для оценки главной части погрешности.
Общая формула для оценки главной части погрешности. - раздел Математика, Обзор возможностей математических пакетов MathCAD 2000, MathLAB 5.0, Mathematica При Численном Решении Математических И Прикладных Задач Почти Неизбежно Появл...
При численном решении математических и прикладных задач почти неизбежно появление на том или ином этапе их решения погрешностей следующих трех типов [1].
а) Погрешность задачи. Она связана с приближенным характером исходной содержательной модели (в частности, с невозможностью учесть все факторы в процессе изучения моделируемого явления), а также ее математического описания, параметрами которого служат обычно приближенные числа (например, из-за принципиальной невозможности выполнения абсолютно точных измерений). Для вычислителя погрешность задачи следует считать неустранимой (безусловной), хотя постановщик задачи иногда может ее изменить.
б) Погрешность метода. Это погрешность, связанная со способом решения поставленной математической задачи и появляющаяся в результате подмены исходной математической модели другой или конечной последовательностью других, например, линейных моделей. При создании численных методов закладывается возможность отслеживания таких погрешностей и доведения их до сколь угодно малого уровня. Отсюда естественно отношение к погрешности метода как к устранимой (или условной).
в) Погрешность округлений (погрешность действий). Этот тип погрешностей обусловлен необходимостью выполнять арифметические операции над числами, усеченными до количества разрядов, зависящего от применяемой вычислительной техники (если, разумеется, не используются специальные программные средства, реализующие, например, арифметику рациональных чисел).
Все три описанных типа погрешностей в сумме дают полную погрешность результата решения задачи. Поскольку первый тип погрешностей не находится в пределах компетенции вычислителя, для него он служит лишь ориентиром точности, с которой следует рассчитывать математическую модель. Нет смысла решать задачу существенно точнее, чем это диктуется неопределенностью исходных данных. Таким образом, погрешность метода подчиняют погрешности задачи. Наконец, при выводе оценок погрешностей численных методов обычно исходят из предположения, что все операции над числами выполняются точно. Это означает, что погрешность округлений не должна существенно отражаться на результатах реализации методов, т.е. должна подчиняться погрешности метода. Влияние погрешностей округлений не следует упускать из виду ни на стадии отбора и алгоритмизации численных методов, ни при выборе вычислительных и программных средств, ни при выполнении отдельных действий и вычислении значений функций [1].
Пусть А и а - два "близких" числа; условимся считать А точным, а — приближенным.
Величина  называется абсолютной погрешностью приближенного числа а, а
называется абсолютной погрешностью приближенного числа а, а  его относительной погрешностью.
его относительной погрешностью.
Числа Δa и δа такие, что Δa > Δа и δа = 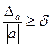 a, называются оценками или границами абсолютной и относительной погрешностей соответственно (к Δa и δа часто применяют также термин "предельные погрешности"). Так как обычно истинные погрешности не известны, то там, где не может возникнуть недоразумений, будем иногда называть Δa и δа просто абсолютной и относительной погрешностями [1].
a, называются оценками или границами абсолютной и относительной погрешностей соответственно (к Δa и δа часто применяют также термин "предельные погрешности"). Так как обычно истинные погрешности не известны, то там, где не может возникнуть недоразумений, будем иногда называть Δa и δа просто абсолютной и относительной погрешностями [1].
Поставим вопрос о грубом оценивании погрешности результата вычисления значения дифференцируемой функции  приближенных аргументов
приближенных аргументов 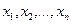 , если известны границы их абсолютных погрешностей
, если известны границы их абсолютных погрешностей  соответственно. В этом случае точные значения аргументов
соответственно. В этом случае точные значения аргументов 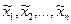 лежат соответственно на отрезках
лежат соответственно на отрезках
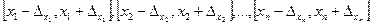 , а точная абсолютная погрешность результата
, а точная абсолютная погрешность результата  есть
есть
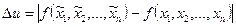
- модуль полного приращения функции. Главной, т.е. линейной частью этого приращения является, как известно, полный дифференциал du . Таким образом, имеем:
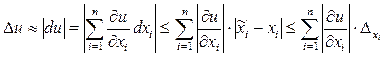 , (2.1)
, (2.1)
т.е. за границу абсолютной погрешности результата приближенно может быть принята величина
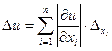 (2.2)
(2.2)
Отсюда легко получается формула приближенной оценки относительной погрешности значения u:
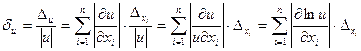 (2.3)
(2.3)
Как частные случаи формул (2.2), (2.3) (точных для функций, линейных относительно xi, или lnxi соответственно) можно получить известные правила оценивания погрешностей результатов арифметических действий [1].
Действительно, пусть 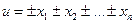 . Тогда
. Тогда 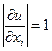 и
и 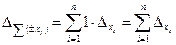 , т.е. при сложении и вычитании приближённых чисел их предельные погрешности складываются.
, т.е. при сложении и вычитании приближённых чисел их предельные погрешности складываются.
Пусть теперь  , где можно считать все сомножители положительными. Так как
, где можно считать все сомножители положительными. Так как  и
и 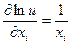 , то, согласно (2.3),
, то, согласно (2.3),
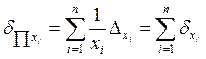 . (2.4)
. (2.4)
Если же 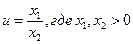 , то
, то  и, значит
и, значит
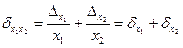 . (2.5)
. (2.5)
Последнее вместе с (2.4) означает известный результат о сложении предельных относительных погрешностей при умножении и делении приближенных чисел.
Возвращаясь к сложению, рассмотрим относительную погрешность суммы n положительных приближенных чисел 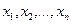 , имеющих границы относительных погрешностей
, имеющих границы относительных погрешностей  соответственно:
соответственно:
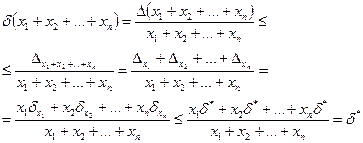 ,
,
где 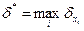 . Полученное неравенство говорит о том, что относительная погрешность суммы n положительных приближённых чисел не превосходит максимальной относительной погрешности слагаемых [1].
. Полученное неравенство говорит о том, что относительная погрешность суммы n положительных приближённых чисел не превосходит максимальной относительной погрешности слагаемых [1].
С вычитанием приближённых чисел дело обстоит хуже: оценка
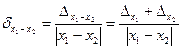
относительной погрешности разности x1 - х2 двух приближенных положительных чисел указывает на возможность сильного возрастания погрешности при x1 - х2 → 0. В этом случае говорят о потере точности при вычитании близких чисел.
2.2.2. Статистический и технический подходы к учёту погрешности действий.
Рассмотренный выше аналитический (или классический) способ учета погрешностей действий, предполагающий точное оценивание погрешностей, основанное либо на приведенных в предыдущем параграфе правилах подсчета погрешностей арифметических действий, либо на параллельной работе с верхними и нижними границами исходных данных, имеет два существенных недостатка. Во-первых, этот способ чрезвычайно громоздок и не может быть рекомендован при массовых вычислениях. Во-вторых, он учитывает крайние, наихудшие случаи взаимодействия погрешностей, которые допустимы, но маловероятны. Ясно, что, например, при суммировании нескольких приближенных чисел (полученных в результате измерений, округлений или каким-либо другим путем) среди них почти наверное будут слагаемые как с избытком, так и с недостатком, т.е. произойдёт частичная компенсация погрешностей. При больших количествах однотипных вычислений вступают в силу уже вероятностные или статистические законы формирования погрешностей результатов действий. Например, методами теории вероятностей показывается, что математическое ожидание абсолютной погрешности суммы n слагаемых с одинаковым уровнем абсолютных погрешностей, при достаточно большом n, пропорционально √n. В частности, если n>10 и все слагаемые округлены до m-го десятичного разряда, то для подсчета абсолютной погрешности суммы 5 применяют правило Чеботарева[1]
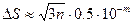 (2.6)
(2.6)
Различие в результатах классического и статистического подходов к оцениванию погрешности суммы рассмотрим на примере оценки погрешности среднего арифметического нескольких приближенных чисел.
Пусть  - среднее арифметическое n (>10) приближенных чисел (например, результатов измерений), имеющих одинаковый уровень абсолютных погрешностей
- среднее арифметическое n (>10) приближенных чисел (например, результатов измерений), имеющих одинаковый уровень абсолютных погрешностей 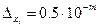 . Тогда классическая оценка абсолютной погрешности величины х есть
. Тогда классическая оценка абсолютной погрешности величины х есть
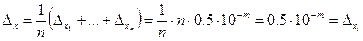 ,
,
т.е. такая же, как и у исходных данных. В тоже время по формуле (2.6) имеем
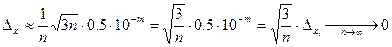 .
.
Как видим, применение правила Чеботарева приводит к естественному выводу о том, что арифметическое усреднение результатов измерений или наблюдений увеличивает точность, чего нельзя сказать на основе классической теории погрешностей [1].
– Конец работы –
Эта тема принадлежит разделу:
Обзор возможностей математических пакетов MathCAD 2000, MathLAB 5.0, Mathematica
Обзор пакета MathCAD... Введение в MathCAD...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Общая формула для оценки главной части погрешности.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов