Non-injective and surjective

·

·

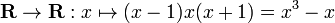
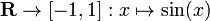
4. In mathematics, the power set (or powerset) of any set S, written 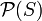, P(S), ℘(S) or 2^S, is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set.

Any subset of 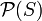is called a family of sets over S.

Example:

If S is the set {x, y, z}, then the subsets of S are:

· {} (also denoted 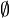, the empty set)

· {x}

· {y}

· {z}

· {x, y}

· {x, z}

· {y, z}

· {x, y, z}

and hence the power set of is^[1]

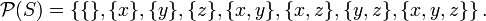
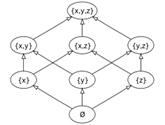The elements of the power set of the set {x, y,z} ordered in respect to inclusion.

In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A (the power set of A) has a strictly greater cardinality than A itself. For finite sets, Cantor's theorem can be seen to be true by a much simpler proof than that given below, since in addition to subsets of A with just one member, there are others as well, and since n < 2ⁿ for all natural numbers n. But the theorem is true of infinite sets as well. In particular, the power set of a countably infinite set is uncountably infinite. The theorem is named for Germanmathematician Georg Cantor, who first stated and proved it.

Proof: Two sets are equinumerous (have the same cardinality) if and only if there exists a one-to-one correspondence between them. To establish Cantor's theorem it is enough to show that, for any given set A, no function f from A into 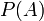, the power set of A, can be surjective, i.e. to show the existence of at least one subset of A that is not an element of the image of A under f. Such a subset, 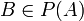, is given by the following construction:

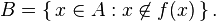
This means, by definition, that for all x in A, x ∈ B if and only if x ∉ f(x). For all x the sets B and f(x) cannot be the same because B was constructed from elements of A whose images (under f) did not include themselves. More specifically, consider any x ∈ A, then either x ∈ f(x) or x ∉ f(x). In the former case, f(x) cannot equal B because x ∈ f(x) by assumption and x ∉ B by the construction of B. In the latter case, f(x) cannot equal B because x ∉ f(x) by assumption and x ∈ B by the construction of B.

Thus there is no x such that f(x) = B; in other words, B is not in the image of f. Because B is in the power set of A, the power set of A has a greater cardinality than A itself.