Equivalence class
Main article: Equivalence class
The set of all a and b for which a ~ b holds make up an equivalence class of X by ~. Let 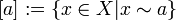 denote the equivalence class to which a belongs. Then all elements of X equivalent to each other are also elements of the same equivalence class.
denote the equivalence class to which a belongs. Then all elements of X equivalent to each other are also elements of the same equivalence class.
13. Real numbers possess an ordering relation. This relation we denote by the symbol “ ” which is read as “greater than”. The axioms of order in
” which is read as “greater than”. The axioms of order in  based on “
based on “ ” are:
” are:
If , then one and only one of the following in true
, then one and only one of the following in true  .
.
If  and
and  , then
, then  .
.
If  and
and 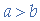 , then
, then  .
.
If  and
and  , then
, then 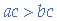 .
.
The following axioms make clear the notion of a point lying between two other points.
1. When B is between A and C then, A, B and C are distinct points lying on a line and B is between C and A.
2. Given a pair of points A and B there is a point C so that B is between A and C.
3. If B lies between A and C then A does not lie between B and C.
4. Let A, B and C be three points on a plane  and a be a line on
and a be a line on  that does not contain any one of these points. If there is a point D on a that is between A and B then either a contains a point between A and C or a contains a point between B and C.
that does not contain any one of these points. If there is a point D on a that is between A and B then either a contains a point between A and C or a contains a point between B and C.
14. A linear order (also called pseudo-order, according to Wikipedia) is the irreflexive version of a total order. A linearly ordered set, or loset, is a set equipped with a linear order.
In classical mathematics, the distinction between linear orders and total orders is merely a terminological technicality, which is not always observed; more precisely, there is a natural bijection between the set of total orders on a given set S and the set of linear orders on S, and one distinguishes them by the notation < (for the linear order) and ≤ (for the total order). In constructive mathematics, however, they are irreducibly different.